МАТЕМАТИКА
Конспект лекций
для студентов заочного обучения направления
«Лесное дело» и «Ландшафтная архитектура»

Брянск 2012
Составители: Баранова И.М., доцент,
Буров П.А., доцент,
Муравьев А.Н., доцент
Рецензенты: Гущин Г.В., к.ф-м.н, доцент БГИТА
Рекомендованы редакционной комиссией
механико – технологического факультета
Протокол № 4 от 04.12.2012 г.
Литература:
1. Баврин И.И. Высшая математика. М.: Просвещение, 1980г.
2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1978г.
3. Зайцев И.Л. элементы высшей математики М.:Наука, 1968г.
4. Данко П.Е., Попов А.Г. высшая математика в упражнениях и задачах. М.: Высшая школа, 1974г.
5. Запорожец Г.И. Руководство к решению задач по математическому анализу. М.: Высшая школа, 1966г.
Определители и системы линейных алгебраических уравнений.
Литература. [2]. Гл. XVII, §1 –7
Под определителем (детерминатором) второго порядка понимается выражение
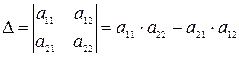
Под определителем третьего порядка понимается выражение

Числа  называются элементами определителя. Индекс
называются элементами определителя. Индекс 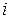 указывает номер строки, а индекс
указывает номер строки, а индекс  - номер столбца на пересечении которых стоит элемент
- номер столбца на пересечении которых стоит элемент  . Так элемент
. Так элемент 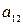 расположен в первой строке и во втором столбце.
расположен в первой строке и во втором столбце.
Пример: 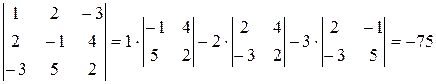
Система вида: 
называется неоднородной линейной системой  алгебраических уравнений с
алгебраических уравнений с 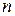 неизвестными. Если все свободные члены, т.е. члены не содержащие неизвестных,
неизвестными. Если все свободные члены, т.е. члены не содержащие неизвестных, 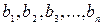 одновременно равны нулю, то система называется однородной. Совокупность значений неизвестных
одновременно равны нулю, то система называется однородной. Совокупность значений неизвестных  при подстановке которых все уравнения системы обращаются в тождества, называется решением системы уравнений.
при подстановке которых все уравнения системы обращаются в тождества, называется решением системы уравнений.
Если система имеет (не имеет ) решение, то она называется совместной (несовместной).
Если система имеет единственное решение, то она называется определенной. Система, имеющая бесконечное множество решений, называется неопределенной.
Решить систему уравнений, значит, найти все ее решения или доказать ее несовместность.
Рассмотрим решение систем линейных алгебраических уравнений методами Крамера и Гаусса на примере системы трех уравнений с тремя неизвестными

I. Метод Крамера.
Если главный определитель системы, т.е. определитель, составленныйиз коэффициентов при неизвестных, отличен от нуля, то эта система совместна и имеет единственное решение, которое находится по формулам Крамера: 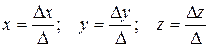 , где
, где 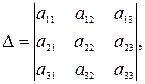

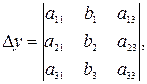

2. Метод Гаусса.
Сущность этого метода состоит в том, что посредством последовательного исключения неизвестных, исходная система преобразуется в эквивалентную ей ступенчатую систему. Для этого используют следующие элементарные преобразования: прибавление к обеим частям одного уравнения системы соответствующих частей другого уравнения системы, умноженных на некоторое число  ; перестановка местами уравнений.
; перестановка местами уравнений.
Пример. Решить систему линейных уравнений двумя способами:
а) методом Гаусса; б) методом Крамера

Решение. a) метод Гаусса – метод последовательного исключения неизвестных. Первое уравнение оставим без изменения, а из второго и третьего исключим первое неизвестное, т.е. 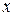 .
.
Для этого последовательно из второго уравнения вычтем первое, а к третьему уравнению прибавим первое, умноженное на -3. Получим эквивалентную систему.

Теперь первое и второе уравнения оставляем без изменения, а из третьего исключим второе неизвестное, т.е.  .
.
Для этого к третьему уравнению прибавим второе, умноженное на 5.
Получим 
Из третьего уравнения получаем 
Подставляя найденное 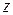 во второе уравнение, получим
во второе уравнение, получим 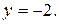
Аналогично, из первого уравнения находим 
б) метод Крамера.
Найдем главный определитель системы
 , так как
, так как  , то система имеет
, то система имеет
единственное решение, которое можно найти по формулам Крамера:
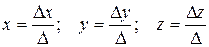 .
.


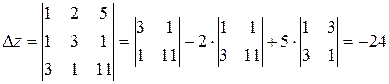
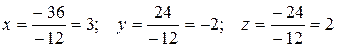
Вопросы для самопроверки.
1. Что называется определителем третьего порядка?
2. Сформулируйте свойства определителей.
3. Дайте определение неоднородной системы линейных уравнений.
4. Что называется решением системы уравнений?
5. Сформулируйте правило Крамера.
6. В чем сущность метода Гаусса?
Векторы.
Литература. [2]. Гл.17. §1-15
Вектором называется направленный отрезок. Всякий ненулевой вектор  характеризуется числовым значением, называемым длиной вектора, т.е.
характеризуется числовым значением, называемым длиной вектора, т.е. 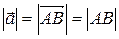 и направлением, задаваемым лучом
и направлением, задаваемым лучом  .
.
Два ненулевых вектора называются коллинеарными, если их направления совпадают или противоположны. Три и более векторов называются компланарными, если они лежат в одной или параллельных плоскостях.
Любой вектор 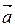 можно разложить единственным образом по базисным векторам
можно разложить единственным образом по базисным векторам  прямоугольной системы координат, т.е. записать
прямоугольной системы координат, т.е. записать  . Коэффициенты
. Коэффициенты  разложения называются координатами вектора
разложения называются координатами вектора  в данной системе координат. Вектор
в данной системе координат. Вектор  с координатами
с координатами  записывают так:
записывают так: 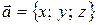 или
или 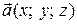 . Длина вектора
. Длина вектора 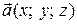 равна
равна  . Если даны
. Если даны  и
и  , то
, то  имеет координаты
имеет координаты 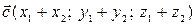 .
.
Скалярным произведением двух ненулевых векторов называют число равное произведению длин этих векторов на косинус угла между ними:  .
.
Если векторы заданы своими координатами в прямоугольной системе координат: 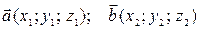 , то
, то  .
.
Векторным произведением двух векторов 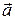 и
и 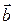 называется такой третий вектор
называется такой третий вектор 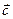 , длина которого численно равны площади параллелограмма, построенного на векторах сомножителях; он перпендикулярен к плоскости параллелограмма и направлен в ту сторону, с которой кратчайшее вращение от
, длина которого численно равны площади параллелограмма, построенного на векторах сомножителях; он перпендикулярен к плоскости параллелограмма и направлен в ту сторону, с которой кратчайшее вращение от 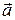 к
к 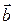 рассматривается совершающимся против часовой стрелки.
рассматривается совершающимся против часовой стрелки.
Если векторы заданы координатами  то векторное произведение их можно найти по формуле:
то векторное произведение их можно найти по формуле: 
Угол между векторами определяется по формуле  или в координатах
или в координатах  .
.
Пример. Даны два вектора 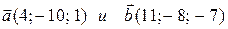 найти угол между этими векторами и вектор
найти угол между этими векторами и вектор  .
.
Решение. Так как векторы заданы в прямоугольной системе координат то для вычисления угла между векторами  и
и 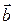 воспользуемся формулой:
воспользуемся формулой:
 .
. 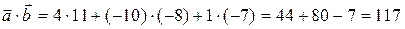 .
.
 ;
;
 .
.
 .
.
Вектор векторного произведения векторов  и
и 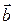 найдем по формуле
найдем по формуле 
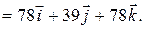
 .
.
Вопросы и упражнения для самопроверки
1. Что называется вектором?
2. Сформулируйте линейные операции над векторами.
3. Дать определение коллинеарности и компланарности векторов.
4. Действия над векторами заданными в координатной форме.
5. Дать определение скалярного произведения векторов
6. Как найти длину вектора?
7. Напишите формулу для вычисления скалярного произведения двух векторов по их прямоугольных координатам.
8. Сформулируйте условия перпендикулярности двух векторов.
9. Напишите формулу для вычисления угла между двумя векторами.
10. Дать определение векторного произведения векторов.
11. Напишите формулу для вычисления векторного произведения векторов заданных координатами.
12. Определите угол между векторами 
13. Найдите длину вектора  , если
, если 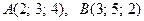 .
.
Прямая на плоскости
Литература. [1] гл. 1. §3-5, [2] гл. 3 §1-7, [3] гл. 3 §11-20.
Имеет место теорема: всякая прямая на плоскости определяется уравнением первой степени с переменными 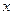 и
и  , и всякое уравнение вида
, и всякое уравнение вида 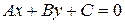 при любых действительных значениях коэффициентов
при любых действительных значениях коэффициентов  , исключая одновременно равенство нулю коэффициентов
, исключая одновременно равенство нулю коэффициентов  и
и  , определяют прямую линию.
, определяют прямую линию.
Уравнение 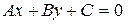 называется общим уравнением прямой. Уравнение прямой, проходящей через данную точку
называется общим уравнением прямой. Уравнение прямой, проходящей через данную точку  с заданным нормальным вектором
с заданным нормальным вектором  :
: 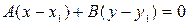 .
.
Уравнение прямой, проходящей через данную точку с заданным направляющим вектором  :
: 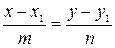 .
.
Уравнение прямой с угловым коэффициентом  . Угловым коэффициентом
. Угловым коэффициентом 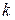 прямой называется тангенс угла наклона прямой к положительному направлению оси
прямой называется тангенс угла наклона прямой к положительному направлению оси 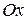 .
.
Уравнение прямой, проходящей через две данные точки  и
и 
 . Две прямые
. Две прямые 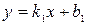 и
и  параллельны тогда и только тогда, когда их угловые коэффициенты равны между собой
параллельны тогда и только тогда, когда их угловые коэффициенты равны между собой  .
.
Две прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно минус единице: 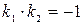 .
.
Если прямые  и
и 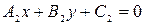 не параллельны то, для нахождения точки их пересечения надо решить систему, составленную из уравнений этих прямых:
не параллельны то, для нахождения точки их пересечения надо решить систему, составленную из уравнений этих прямых: 
Пример. Даны вершины треугольника  . Составить уравнение высоты, опущенной из вершины
. Составить уравнение высоты, опущенной из вершины  на сторону
на сторону 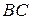 и уравнение медианы, проведенной из вершины
и уравнение медианы, проведенной из вершины  . Сделайте чертеж.
. Сделайте чертеж.
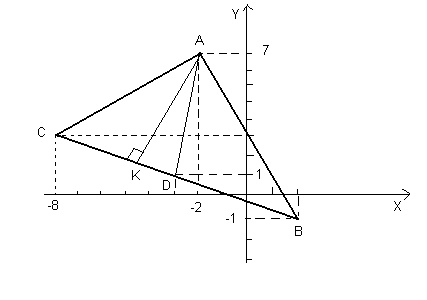 Решение.
Решение.
Найдем угловые коэффициенты прямых  и
и 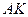 .
. 
 .
.
Так как  то
то  . Тогда уравнение высоты
. Тогда уравнение высоты  запишем по формуле
запишем по формуле  ,
, 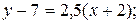
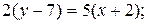
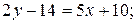
 - уравнение высоты
- уравнение высоты  . Найдем координаты точки
. Найдем координаты точки 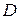 , делящей отрезок
, делящей отрезок 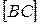 пополам:
пополам: 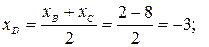
 ;
;  . Запишем уравнение медианы
. Запишем уравнение медианы  по формуле:
по формуле:  ;
;  ;
;  ;
;  ;
;  - уравнение медианы
- уравнение медианы 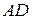 .
.
Вопросы и упражнения для самопроверки.
1. Напишите общее уравнение прямой.
2. Напишите уравнение прямой с угловым коэффициентом.
3. Сформулируйте условия параллельности и перпендикулярности прямых.
4. Напишите формулу для вычисления угла между двумя прямыми.
5. Как найти точку пересечения двух прямых?
6. Составьте уравнения прямой проходящей через точки  и
и 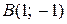 .
.
7. Дана прямая 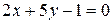 . Напишите уравнение прямой, проходящей через точку
. Напишите уравнение прямой, проходящей через точку  перпендикулярно данной прямой.
перпендикулярно данной прямой.
Функции. Предел функции.
Литература. [1], гл. 2 §8-13, [2] гл. 6 §2, 4, 6-9. гл. 7 §3-13, [3] гл. 5, §40-51.
Если каждому значению переменной величины 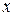 по некоторому закону ставится в соответствие одно определенное значение переменной
по некоторому закону ставится в соответствие одно определенное значение переменной 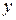 , то говорят, что
, то говорят, что 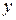 есть однозначная функция
есть однозначная функция 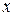 , и обозначается
, и обозначается  .
.
Число  называется пределом функции
называется пределом функции 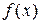 при
при 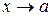 , если для любого
, если для любого 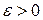 существует
существует  такое, что
такое, что  при
при 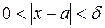 . Обозначается так:
. Обозначается так:  .
.
Если существуют  и
и 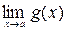 , то имеют место следующие теоремы:
, то имеют место следующие теоремы:
1. 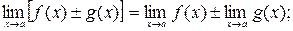
2. 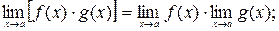
3. 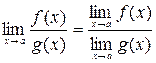 , при
, при 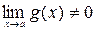 . Частое применение находят следующие пределы:
. Частое применение находят следующие пределы: 

Пример. Вычислить пределы: а) 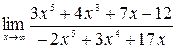 ; б)
; б)  ;
;
в)  .
.
Решение.
а) В данном примере нельзя непосредственно воспользоваться теоремой о пределе частного, так как пределы числителя и знаменателя равны бесконечности. Для раскрытия неопределенности данного вида вынесем в числителе и знаменателе 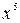 за скобки, имеем
за скобки, имеем 

б) При непосредственной подстановке убеждаемся, что предел числителя и знаменателя равен нулю. Имеет место неопределенность  . Для раскрытия ее разложим числитель на множители. Получим
. Для раскрытия ее разложим числитель на множители. Получим 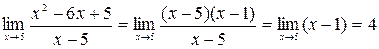 .
.
в) При  числитель и знаменатель стремится к нулю, т.е. имеет место неопределенность
числитель и знаменатель стремится к нулю, т.е. имеет место неопределенность  .
. 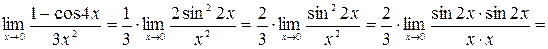
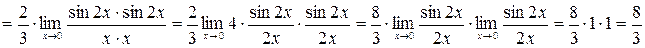 .
.
Здесь использовали то, что 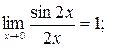
Вопросы и упражнения для самопроверки.
1. Дайте определение функции.
2. Что называется областью определения функции?
3. Каковы способы задания функции?
4. Дайте определение предела функции.
5. Какая величина называется бесконечно малой?
6. Сформулируйте основные теоремы о пределах.
7. Сформулируйте первый замечательный предел.
8. Вычислите пределы:  ,
, 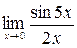 ,
,  ,
, 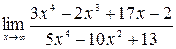 .
.
9. Какие бесконечно малые называются эквивалентными?
Производная и ее приложения.
Литература. [1] гл.3 §14-17. [2] гл.9 §1-5, гл.10 §1-15, [3] гл. 7 §60-66 гл. 8 §67-85
Производной функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
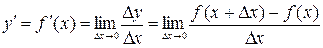 . Функция, имеющая конечную производную, называется дифференцируемой, а операция нахождения производной - дифференцированием.
. Функция, имеющая конечную производную, называется дифференцируемой, а операция нахождения производной - дифференцированием.
Если 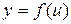 и
и  - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции  существует и равна
существует и равна 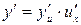 .
.
Таблица формул дифференцирования:
1. 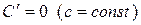 12.
12. 
2.  13.
13. 
3.  14.
14. 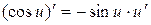
4.  15.
15. 
5.  16.
16. 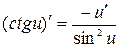
6. 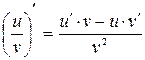 17.
17. 
7. 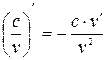 18.
18. 
8. 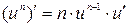 19.
19. 
9.  20.
20. 
10. 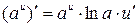 21.
21. 
11. 
Здесь  и
и 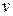 дифференцируемые функции от
дифференцируемые функции от  , а
, а  – постоянная.
– постоянная.
Геометрический смысл производной
Производная функция  представляет собой угловой коэффициент касательной, проведенной к графику функции в любой ее точке.
представляет собой угловой коэффициент касательной, проведенной к графику функции в любой ее точке.
Уравнение касательной, проведенной к графику функции 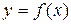 в точке
в точке 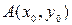 имеет вид
имеет вид 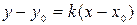 , где
, где  ,
, 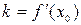 .
.
Физический смысл производной. Если тело движется прямолинейно по закону 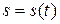 , то производная пути
, то производная пути 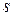 по времени
по времени 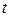 равна скорости движения тела в данный момент времени
равна скорости движения тела в данный момент времени 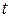 :
:  .
.
Производной второго порядка функции  называется производная от первой производной, т.е.
называется производная от первой производной, т.е.  .
.
Физический смысл второй производной. Если тело движется прямолинейно по закону 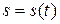 , то вторая производная пути
, то вторая производная пути 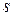 по времени
по времени 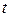 равна ускорению движения тела в данный момент времени
равна ускорению движения тела в данный момент времени 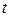 :
:  .
.
Пример. Найти производные функций:
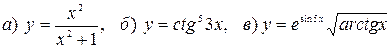 .
.
Решение. а) дифференцируем функцию по формуле  ,
,
 .
.
б) воспользуемся формулой дифференцирования сложной функции:  , получим
, получим 
 .
.
в) 
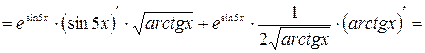

 .
.
Вопросы и упражнения для самопроверки.
1. Дайте определение производной.
2. Запишите формулы производной произведения, частного.
3. В чем состоит геометрический смысл производной?
4. Как найти скорость движения тела, если задан закон прямолинейного движения?
5. Запишите уравнение касательной к кривой  в точке
в точке  .
.
6. В чем состоит физический смысл второй производной?
7. Запишите формулу производной сложной функции.
8. Найдите  , если
, если  .
.
Приложения производной к исследованию функций.
Литература. [1] гл. 3 § 18,19, [2] гл. 11 § 1,2, 7-10, [3] гл. 9 §86-96.
Дифференцируемая функция 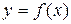 возрастает на промежутке
возрастает на промежутке 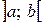 , если ее производная положительна в каждой точке этого промежутка.
, если ее производная положительна в каждой точке этого промежутка.
Дифференцируемая функция 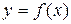 убывает на промежутке
убывает на промежутке 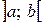 , если ее производная отрицательна в каждой точке этого промежутка.
, если ее производная отрицательна в каждой точке этого промежутка.
Функция 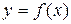 имеет в точке
имеет в точке  максимум, если для всех
максимум, если для всех  , достаточно близких к
, достаточно близких к  , выполняется неравенство
, выполняется неравенство 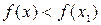 .
.
Функция 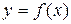 имеет в точке
имеет в точке  минимум, если для всех значений
минимум, если для всех значений  достаточно близких к
достаточно близких к  , выполняется неравенство
, выполняется неравенство 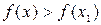 . Точки максимума и минимума называются точками экстремума.
. Точки максимума и минимума называются точками экстремума.
Необходимое условие экстремума функции.
Если в точке  дифференцируемая функция имеет экстремум, то в этой точке
дифференцируемая функция имеет экстремум, то в этой точке 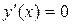 . Точки в которых
. Точки в которых  называются критическими.
называются критическими.
Первое достаточное условие существования экстремума функций. Если при перехода через критическую точку  производная меняет знак, то
производная меняет знак, то  точка экстремума. При этом если производная меняет знак с плюса на минус, то
точка экстремума. При этом если производная меняет знак с плюса на минус, то  точка максимума, а
точка максимума, а 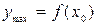 . Если же производная меняет знак с минуса на плюс, то
. Если же производная меняет знак с минуса на плюс, то  точка минимума, а
точка минимума, а  .
.
Говорят, что на промежутке  кривая обращена выпуклостью вверх, или выпукла, если она лежит ниже касательной, проведенной в любой ее точке.
кривая обращена выпуклостью вверх, или выпукла, если она лежит ниже касательной, проведенной в любой ее точке.
Говорят, что кривая на промежутке 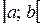 обращена выпуклостью вниз или вогнута, если она лежит выше касательной, проведенной в любой ее точке.
обращена выпуклостью вниз или вогнута, если она лежит выше касательной, проведенной в любой ее точке.
Точка, в которой меняется направление вогнутости кривой, называется точкой перегиба.
График дифференцируемой функции 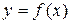 является вогнутым на промежутке
является вогнутым на промежутке  , если вторая производная функции положительна в каждой точке этого промежутка.
, если вторая производная функции положительна в каждой точке этого промежутка.
График дифференцируемой функции 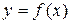 является выпуклым на промежутке
является выпуклым на промежутке  , если вторая производная функции отрицательна в каждой точке этого промежутка.
, если вторая производная функции отрицательна в каждой точке этого промежутка.
Необходимым условием точки перегиба дифференцируемой функции является равенство нулю второй производной, а достаточным условием является то, что при переходе через эту точку  меняет знак.
меняет знак.
Прямая  является вертикальной асимптотой, если
является вертикальной асимптотой, если  . Уравнение наклонной асимптоты имеет вид
. Уравнение наклонной асимптоты имеет вид 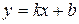 , где
, где  ,
, 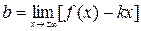 , при условии, что оба эти предела существуют.
, при условии, что оба эти предела существуют.
Исследование функции в построение графиков можно проводить по следующей схеме:
1. Найти область определения функции.
2. Установить нечетность, четность и периодичность функции.
3. Найти точки разрыва.
4. Найти асимптоты.
5. Найти промежутки монотонности и экстремумы функции.
6. Найти направление вогнутости и точки перегиба.
7. Найти точки пересечения графика функции с осями координат и при необходимости, несколько дополнительных точек.
8. Построить график, используя результаты исследования.
Пример. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Функция определена для всех значений  , кроме
, кроме  .
.  , следовательно, функция четная и график ее будет симметричен относительно оси
, следовательно, функция четная и график ее будет симметричен относительно оси 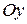 .
.  и
и  - вертикальные асимптоты.
- вертикальные асимптоты.
Найдем наклонные асимптоты 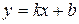 .
. 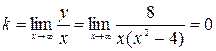 ,
, 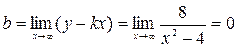 . Таким образом, прямая
. Таким образом, прямая 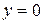 является горизонтальной асимптотой. Найдем интервалы возрастания, убывания функции и точки экстремума.
является горизонтальной асимптотой. Найдем интервалы возрастания, убывания функции и точки экстремума. 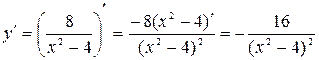 . Находим критические точки, где
. Находим критические точки, где  .
. 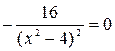 ;
;  ;
; 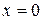 . Производная
. Производная 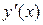 не определена при
не определена при 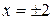 . Область определения функции разбивается на четыре участка монотонности.
. Область определения функции разбивается на четыре участка монотонности.
При 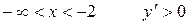 , следовательно, функция возрастает.
, следовательно, функция возрастает.
При  , следовательно, функция возрастает.
, следовательно, функция возрастает.
При  - функция убывает.
- функция убывает.
При  - функция убывает.
- функция убывает.
При переходе через точку 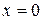
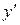 меняет знак с
меняет знак с  на -, следовательно,
на -, следовательно,  будет точкой максимума.
будет точкой максимума.  .
.
Найдем интервалы выпуклости, вогнутости и точки перегиба. 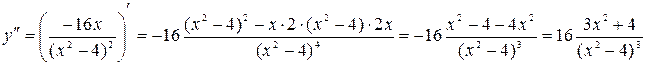 .
.
 не существует при
не существует при 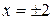 .
.
При 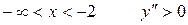 , следовательно, график вогнутый.
, следовательно, график вогнутый.
При 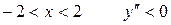 следовательно, на этом интервале график выпуклый.
следовательно, на этом интервале график выпуклый.
При 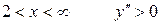 следовательно, график вогнутый.
следовательно, график вогнутый.
Точек перегиба график не имеет. Построим график.

Вопросы и упражнения для самопроверки.
1. Сформулируйте необходимые условия экстремума функции.
2. Как найти промежутки возрастания и убывания функции?
3. В чем состоит достаточное условие экстремума?
4. Как найти промежутки выпуклости и вогнутости кривой?
5. Как найти точки перегиба кривой?
6. Найдите точки экстремума функции: 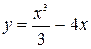
Неопределенный интеграл.
Литература. [1] гл. 4 §20, 21, 28 упр1-89 [2] гл.11 §102-104 [3] гл. 13 §1-5, 10, упр. 1-32.
Как известно основная задача дифференциального исчисления сводится к нахождению по заданной функции ее производной. Неопределенный интеграл решает обратную задачу: по заданной производной находят первоначальную функцию.
Функцию  называют первообразной для функции
называют первообразной для функции 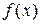 в интервале
в интервале 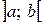 , если
, если 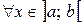 имеет место равенство
имеет место равенство 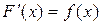 . Так для функции
. Так для функции 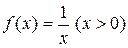 первообразной служит функция
первообразной служит функция 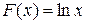 , так как для любого
, так как для любого  ; для функции
; для функции 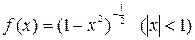 первообразной является функция
первообразной является функция 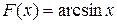 поскольку
поскольку 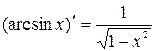
 и т.д.
и т.д.
Если  -первообразная для функции
-первообразная для функции 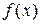 , то множество функций
, то множество функций  , где
, где  - произвольная постоянная, называют неопределенным интегралом от функции
- произвольная постоянная, называют неопределенным интегралом от функции 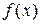 и обозначают символом
и обозначают символом 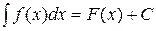 .
.
Например,  , так как
, так как 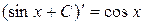 .
.
Приведем основные свойства неопределенных интегралов (Н.И.).
1. Производная от Н.И. равна подынтегральной функции, а дифференциал -подынтегральному выражению, т.е. 
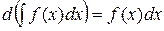 .
.
2. Н.И. от дифференциала функции равен этой функции плюс произвольное постоянное, т.е.  .
.
3. Постоянный множитель можно выносить за знак Н.И.: 
4. Н.И.от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов:  .
.
Таблица простейших интегралов имеет вид:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 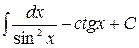
9. 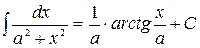 10.
10. 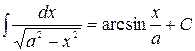
11. 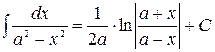
Основными методами интегрирования являются: разложения, подстановки, по частям. Интегрирование методом разложения заключается в приведении данного интеграла (по свойству 4) к сумме более простых или табличных интегралов. Метод подстановки имеет в виду следующее: положив в интеграле 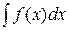
 ,
, 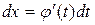 получим
получим  . При интегрировании по частям берут формулу дифференциала произведения:
. При интегрировании по частям берут формулу дифференциала произведения: 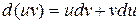 и из нее после интегрирования обеих частей получают формулу
и из нее после интегрирования обеих частей получают формулу  . Эта формула применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функций, например:
. Эта формула применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функций, например:  или
или  .
.
При этом за  принимают функцию, которая дифференцированием упрощается, а за
принимают функцию, которая дифференцированием упрощается, а за 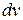 т
т