Коллоквиум 2
Производные
1. Определение производной функции.
Определение: производной функции в точке  называется предел отношения приращения функции
называется предел отношения приращения функции  к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента  в этой точке при
в этой точке при 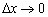 . Или коротко:
. Или коротко:
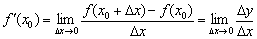
2. Геометрический и механический смысл производной.
Геометрический смысл производной. производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
уравнение касательной:
y = f (x 0) + f ’(x 0) · (x – x 0).
Механический смысл производной. ускорение – это производная скорости по времени: a = v’ (t).
3. Определение функции, дифференцируемой в точке.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , предельной для множества E, если ее приращение Δ f (x 0), соответствующее приращению аргумента x, может быть представлено в виде
, предельной для множества E, если ее приращение Δ f (x 0), соответствующее приращению аргумента x, может быть представлено в виде
Δ f (x 0) = A (x 0)(x - x 0) + ω (x - x 0), (1)
где ω (x - x 0) = о (x - x 0) при x → x 0.
4. Связь между дифференцируемостью и существованием производной.
Теорема 1. Если функция дифференцируема в некоторой точке, то в этой точке она имеет дифференциал.
Доказательство. Функция  - дифференцируема в точке х 0,
- дифференцируема в точке х 0,
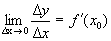 .
.
По теореме о связи предела и б.м. функции:
 ,
,
где  - б.м. функция
- б.м. функция
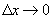 .
. Умножим обе части на D х:
 ,
,
 - б.м. функция более высокого порядка, чем Dх.
- б.м. функция более высокого порядка, чем Dх.
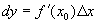 .
.
Следовательно, функция имеет дифференциал и  .
.
Теорема 2. Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке.
Доказательство. Пусть функция имеет дифференциал  . Тогда
. Тогда
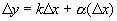 .
.
Разделим обе части на D х:
 .
.
Переходя к пределу при 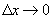 , получим
, получим
 .
.
Таким образом, функция имеет производную и  .
.
Из этих теорем следует, что 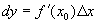 .
.
5. Связь между дифференцируемостью и непрерывностью.
Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство. Пусть функция у=f(x) дифференцируема в точке х0. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу. Найдем  .
.
 .
.
Следовательно, у=f(x) непрерывна в точке х 0.
Следствие. Если х0 – точка разрыва функции, то в ней функция не дифференцируема.
Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.
Пример. у=|х|, х0=0.
 Y
Y
0 X
Dх>0,  ;
;
Dх<0,  .
.
В точке х 0 = 0функция непрерывна, но производной не существует.
6. Таблица производных
7. Правила дифференцирования.
. 
8. Производная сложной функции.

9. Логарифмическое дифференцирование.
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.
10. Дифференциал.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
произвольное бесконечно малое приращение переменной величины.
11. Геометрический смысл дифференциала.
Дифференциал функции y = f (x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину  (см. рисунок).
(см. рисунок).
12. Производные высшего порядка.
Если функция  имеет производную в каждой точке
имеет производную в каждой точке  своей области определения, то ее производная
своей области определения, то ее производная  есть функция от
есть функция от  . Функция
. Функция 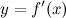 , в свою очередь, может иметь производную, которую называют производной второго порядка функции
, в свою очередь, может иметь производную, которую называют производной второго порядка функции  (или второй производной) и обозначают символом
(или второй производной) и обозначают символом 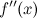 . Таким образом
. Таким образом

13. Формула Лейбница.
 =
= 
14. Дифференциалы высших порядков.
Дифференциалом -го порядка
-го порядка 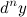 функции
функции  называется дифференциал от дифференциала
называется дифференциал от дифференциала 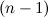 -го порядка этой функции, то есть
-го порядка этой функции, то есть

15. Теорема Ферма.
Короче говоря, великая теорема Ферма утверждает, что уравнение xn+yn=zn не имеет натуральных решений при n > 2. Всего-навсего.
16. Теорема Ролля.
Теорема 1. (Теорема Ролля) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b);
3. на концах отрезка [a, b] принимает равные значения.
Тогда существует точка c Î (a, b) такая, что f'(c) = 0.
17. Теорема Лагранжа.
Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
1. непрерывна на отрезке [a, b];
2. дифференцируема в интервале (a, b).
Тогда существует точка с Î (a, b) такая, что
| f(b) − f(a) = f '(c) · (b − a). |
18. Теорема Коши.
Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)
1. непрерывны на отрезке [a, b];
2. дифференцируемы в интервале (a, b);
3. "x Î (a, b) g'(x) ≠ 0.
Тогда существует точка c Î (a, b) такая, что
|
= . |
19. Формула конечных приращений.
f(b) − f(a) = f '(c) · (b − a). Теорема Лагранжа
20. Теоремы Лопиталя.
(Правило Лопиталя).
Пусть функции  и
и  удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки
, кроме, может быть, самой точки  ;
;
2)  и
и  в этой окрестности;
в этой окрестности;
3)  ;
;
4)  существует конечный или бесконечный.
существует конечный или бесконечный.
Тогда существует и  , причем
, причем 
21. Необходимое условие возрастания (убывания) функции.
Необходимое условие возрастания функции. Если функция y = f (х) дифференцируема и возрастает на интервале [а, b], то f '(х) > 0 для всех х из этого интервала.
Необходимое условие убывания функции. Если функция у = f (х) дифференцируема и убывает на интервале [а, b], то f(х)<0 для всех х из этого интервала.
22. Достаточное условие возрастания (убывания) функции.
Достаточное условие возрастания (убывания функции). Пусть функция у = f (x) дифференцируема на интервале [а, b], Если во всех точках этого интервала f(x)>0, то функция возрастает на этом интервале, а если f(х)<0, то функция убывает на этом интервале.
23. Экстремум функции.
Точки экстремума – точки минимума и максимума.
Точка x = x0 называется точкой максимума, а число f(x0) — максимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство f(x0)>f(x).
Точка x = x0 называется точкой минимума, а число f(x0) — минимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство f(x0)< f(x).
24. Необходимое условие существования экстремума.
Если x0 — точка экстремума, то производная в этой точке равна нулю или не существует.
25. Достаточное условие существования экстремума.
Если функция y=f(x) непрерывна в точке x = x0, дифференцируема в некоторой окрестности этой точки, и при переходе через точку x0 производная f'(x) меняет знак, то x = x0 — точка:
а) f(x0) — максимум, если f'(x)>0, при x<x0 и f'(x)<0, при x>x0.
б) f(x0) — минимум, если f'(x)<0, при x<x0 и f(x0)>0, при x<x0.
26. Достаточное условие существования экстремума (вторая производная).
Пусть дана функция  , она определена в некоторой окрестности точки
, она определена в некоторой окрестности точки  , ее первая производная
, ее первая производная  и пусть
и пусть  , тогда:
, тогда:
- Если
 , то точка
, то точка  – точка строгого минимума;
– точка строгого минимума; - Если
 , то точка
, то точка  – точка строгого максимума.
– точка строгого максимума.
27. Определение графика функции, выпуклого вверх (вниз).
Определение. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Определение.Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
28. Достаточное условие существования точки перегиба.
Первое достаточное условие перегиба.
После того как найдены все  , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.
, которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.
Пусть функция y=f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки
, имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от
. Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то
, вторая производная имеет разные знаки, то  является точкой перегиба графика функции.
является точкой перегиба графика функции.
Как видите первое достаточное условие не требует существования второй производной в самой точке  , но требует ее существование в окрестности точки
, но требует ее существование в окрестности точки  .
.
29. Необходимое условие существования точки перегиба.
Сформулируем необходимое условие перегиба графика функции.
Пусть график функции y=f(x) имеет перегиб в точке  и имеет при
и имеет при  непрерывную вторую производную, тогда выполняется равенство
непрерывную вторую производную, тогда выполняется равенство 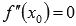 .
.
Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения  , в которых вторая производная равна нулю, являются абсциссами точек перегиба.
, в которых вторая производная равна нулю, являются абсциссами точек перегиба.
Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все  из области определения функции, для которых
из области определения функции, для которых  и
и  . Обычно это точки, в которых знаменатель первой производной обращается в ноль.
. Обычно это точки, в которых знаменатель первой производной обращается в ноль.
30. Достаточное условие выпуклости вверх (вниз) графика функции.
Теорема 1 (достаточное условие точки выпуклости). Если функция f (x) во всех точках интервала (a, b) имеет отрицательную вторую производную, т.е. f ″(х) < 0, то график функции в этом интервале выпуклый вверх. Если же f ″(x) > 0 для всех х є (a, b), то график функции выпуклый вниз в этом интервале.
Доказательство. Пусть f″(х) < 0 для любого х є (a, b). Возьмем на графике произвольную точку М с абсциссой х0 є (a, b) и проведем через М касательную (рис. 16).

31. Асимптоты графика.
Определение
Прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  или
или  равно
равно 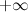 или
или  .
.
Замечание. Прямая  не может быть вертикальной асимптотой, если функция непрерывна в точке
не может быть вертикальной асимптотой, если функция непрерывна в точке  . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая 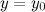 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  или
или  равно
равно  .
.