Этот вопрос можно предложить учащимся в качестве самостоятельной работы.
I.
а) Составьте всевозможные сочетания по 2 элемента без повторений из элементов множества М={а, б, в, г, д}. Для каждого из составленных подмножеств выпишите дополнения - трехэлементные подмножества оставшихся элементов - и сравните число тех и других. Какой вывод можно сделать о числах 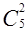 и
и 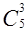 ?
?
б)Из n элементов некоторого множества составлены всевозможные k-элементные подмножества и соответствующие им дополнения — (n-k) – элементные подмножества оставшихся элементов. Какой вывод можно сделать о сравнительной величине чисел 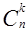 и
и 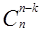 ?
?
в) Воспользуйтесь формулой подсчета числа сочетаний без повторений и докажите равенство 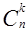 =
= 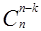 . Это равенство выражает одно из важных свойств сочетаний. Им удобно пользоваться для вычисления
. Это равенство выражает одно из важных свойств сочетаний. Им удобно пользоваться для вычисления 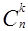 в случае k>
в случае k> 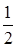 n.
n.
г) Не производя вычислений, выберите равные из следующих чисел: 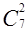 ,
, 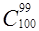 ,
, 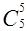 ,
, 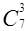 ,
, 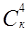 ,
, 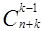 ,
, 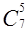 ,
, 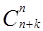 ,
, 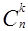 ,
, 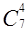 ,
, 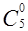 ,
, 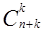 ,
, 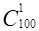 ,
, 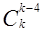 .
.
д) Вычислите 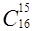 ,
, 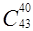 ,
, 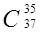 .
.
е) Множество М={а, б, в, г, д, е} разбейте всеми возможными способами на два подмножества так, чтобы в одно из них входило 2 элемента, а в другое - 4.
ж) Из 12 человек нужно составить 2 волейбольные команды по 6 человек в каждой. Сколькими способами это может быть сделано?
II. Докажите следующее свойство сочетаний:
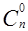 +
+ 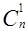 +
+ 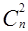 +…+
+…+ 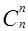 =2n.
=2n.
а) Возьмите множество М={а, b, с} из трех элементов и составьте k-элементные подмножества М /k=0, 1, 2, 3/.
Каждому подмножеству поставьте в соответствие последовательность из трех цифр – единиц и нулей – следующим образом: каждому из трех элементов а, b, с поставьте в соответствие 1, если он входит в подмножество, 0 – если он в подмножество не входит. Рассмотрите таблицу
Таблица 1.
| Виды подмножеств | Число подмнож. | Подмножества | Последовательности из 1 и 0 |
| Пустые | 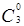
| Æ | |
| Одноэлементные | 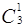
| {a}, {b}, {c} | 100, 010,001 |
| Двухэлементные | 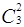
| {ab}, {ac}, {bc} | 110, 101,011 |
| Трехэлементные | 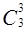
| {a, b, c}| |
Число всех подмножеств множества М равно 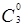 +
+ 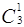 +
+ 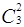 +
+ 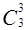 и равно числу всех последовательностей длины три из единиц и нулей. Число таких последовательностей нетрудно подсчитать: каждое из трех мест в последовательности может быть занято 1 или 0, то есть двумя способами, а все три места – по принципу умножения – 2×2×2=23 способами. Это число можно получить и по формуле подсчета числа размещений с повторением, таким образом,
и равно числу всех последовательностей длины три из единиц и нулей. Число таких последовательностей нетрудно подсчитать: каждое из трех мест в последовательности может быть занято 1 или 0, то есть двумя способами, а все три места – по принципу умножения – 2×2×2=23 способами. Это число можно получить и по формуле подсчета числа размещений с повторением, таким образом, 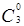 +
+ 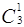 +
+ 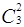 +
+ 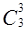 =23.
=23.
б) Проведите аналогичные рассуждения для множества из n элементов. Тогда какие изменения следует внести в таблицу? Сделайте вывод, результат запишите.
Занятие №9. Свойство сочетаний 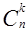 =
= 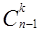 +
+ 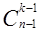 и треугольник Паскаля.
и треугольник Паскаля.
I. Для изучения следующего свойства сочетаний предварительно составим трехэлементные подмножества множества М={а, б, в, г, д}. Затем выберем из множества М любой элемент, например, «а» и разобьем все подмножества на два класса: не содержащие «а» и содержащие «а».
I класс: {б, в, г}, {б, в, д}, {б, г, д}, {в, г, д}
II класс: {а, б, в}, {а, б, г}, {а, б, д}, {а, в, г},
{а, в, д}, {а, г, д}.
Первый класс состоит из всевозможных сочетаний без повторений по три элемента из следующих четырех: б, в, г, д. Таких сочетаний 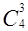 . Каждое подмножество второго класса состоит из элемента «а» и двух элементов, выбираемых из множества следующих элементов: б, в, г, д. Очевидно, число таких подмножеств равно
. Каждое подмножество второго класса состоит из элемента «а» и двух элементов, выбираемых из множества следующих элементов: б, в, г, д. Очевидно, число таких подмножеств равно 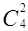 .
.
Подмножества I и II классов исчерпывают все трехэлементные подмножества множества М, что означает:
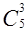 =
= 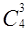 +
+ 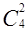 .
.
Аналогичными рассуждениями получите равенство:
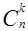 =
= 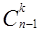 +
+ 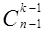 .
.
Убедитесь в справедливости последнего равенства, воспользовавшись формулой подсчета числа сочетаний без повторений.
II. Составим таблицу значений 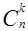 при различных значениях n и k. В таблицу 2 занесем значения
при различных значениях n и k. В таблицу 2 занесем значения 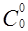 =1,
=1, 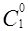 =1,
=1, 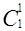 =1,
=1, 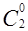 =1,
=1, 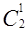 =2,
=2, 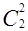 =1. Заполните остальные строки таблицы, используя свойство сочетаний.
=1. Заполните остальные строки таблицы, используя свойство сочетаний.
Займемся изучением таблицы 2.
Первые и последние элементы любой строки равны 1, так как 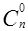 =
= 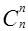 =1. Это равенство будем считать верным и при n=0 (пустое множество своим единственным подмножеством имеет самое себя).
=1. Это равенство будем считать верным и при n=0 (пустое множество своим единственным подмножеством имеет самое себя).
Любой другой элемент таблицы 2 согласно свойству сочетаний, на основании которого составлена таблица, равен сумме двух элементов предшествующей строки: стоящего непосредственно над ним и стоящего над ним слева.
Часто числа 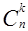 располагают в таблице иначе, так, что каждый элемент таблицы равен сумме двух чисел предшествующей строки, стоящих непосредственно над ним слева и справа. Тогда таблица принимает форму равнобедренного треугольника.
располагают в таблице иначе, так, что каждый элемент таблицы равен сумме двух чисел предшествующей строки, стоящих непосредственно над ним слева и справа. Тогда таблица принимает форму равнобедренного треугольника.
Исследованием свойств такой треугольной таблицы и применениями ее занимался выдающийся ученый Франции Блез Паскаль (1623 —1662). Поэтому рассматриваемую таблицу часто называют треугольником Паскаля. Хотя задолго до Паскаля этот треугольник встречался в работах итальянских и арабских математиков.
Отметим некоторые из свойств треугольника Паскаля.
1. Сумма чисел k-той строки равна 2k: ранее было доказано, что 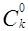 +
+ 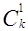 +
+ 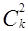 +…+
+…+ 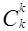 =2k.
=2k.
Таблица 2
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | ||||||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … |
2. Числа каждой строки треугольника, равноудаленные от ее концов, равны между собой. Обоснованием этого свойства служит равенство 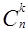 =
= 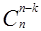 .
.
2. Члены любой строки треугольника Паскаля до середины строки возрастают, а затем убывают.
Задания:
1. Сколько различных подмножеств имеет множество всех цифр?
2. Сколько различных делителей, включая 1, имеет число а)2∙3∙5∙7∙11? б) 195?
3. Сколько различных произведений, кратных 10, можно составить из множителей 2, 7, 11, 9, 3, 5?
4. С помощью свойства сочетаний 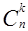 =
= 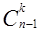 +
+ 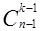 докажите равенство:
докажите равенство: 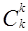 +
+ 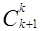 +
+ 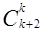 +…+
+…+ 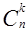 =
= 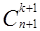 .
.
5. Пользуясь треугольником Паскаля, найдите числа 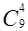 ,
, 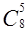 .
.
6. Напишите 11 строку треугольника Паскаля.