Пусть в нашем распоряжении имеются два различных объекта. Или элемента. Совершенно любые. Два яблока (красное и зелёное), две конфеты (шоколадная и карамель), две книги, две цифры, две буквы – всего чего угодно. Лишь бы они были различными. Назовём их A и B соответственно.
Что можно с ними делать? Будем их располагать в различном порядке.
Каждое такое расположение называется перестановкой без повторений. Почему «без повторений»? Потому, что все элементы, участвующие в перестановке, различны. Это мы пока что для простоты так решили. Есть ещё перестановка с повторениями, где некоторые элементы могут быть одинаковыми. Но такие перестановки чуть сложнее.
Итак, если рассматривается два различных элемента, то возможны такие варианты:
AB, BA.
Всего два варианта, т.е. две перестановки.
А теперь добавим к нашему набору ещё один элемент C. В этом случае перестановок станет уже шесть:
ABC, ACB, BAC, BCA, CAB, CBA.
Идём дальше. Добавляем ещё один элемент D.
Перестановки из четырёх элементов будем строить так. Сначала на первое место поставим элемент A. При этом оставшиеся три элемента можно переставить, как нам уже известно, шестью способами:
Значит, число перестановок с первым элементом A равно 6.
Но та же самая история будет получаться, если мы на первое место поставим любой из этих четырёх элементов. Они же равноправны и каждый заслуживает оказаться на первом месте. Значит, общее число перестановок из четырёх элементов будет равно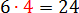 
. Вот они:
Итак, подытожим: перестановкой из n элементов называется любой упорядоченный набор из этих n элементов.
Слово «упорядоченный» здесь является ключевым: каждая перестановка различается только порядком элементов, а сами элементы в наборе остаются прежними.
Осталось только выяснить, чему равно количество таких перестановок из любого числа элементов: чтобы каждый раз не выписывать все различные варианты и их подсчитывать. Для 4-х элементов мы получили 24 перестановки – это уже довольно много для наглядного восприятия. А если элементов 10? Или 100? Хорошо бы сконструировать формулу, которая одним махом подсчитывала бы число всех таких перестановок для любого числа элементов. И такая формула есть! Сейчас мы её выведем. Но для начала сформулируем одно очень важное во всей комбинаторике вспомогательное правило, называемое правилом произведения.
Правило произведения: если в наборе имеется n различных вариантов выбора первого элемента и для каждого из них есть m различных вариантов выбора второго элемента, то всего можно составить n·m различных пар из этих элементов.
А теперь, пусть теперь имеется набор из n различных элементов
,
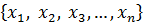где, естественно,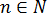 
. Нам нужно подсчитать число всех возможных перестановок из элементов этого набора. Рассуждаем точно так же. На первое место можно поставить любой из этих n элементов. Это значит, что число способов выбрать первый элемент равно n.
Теперь представим, что первый элемент у нас выбран (n способами, как мы помним). Сколько невыбранных элементов осталось в наборе? Правильно, n-1. Это значит, что второй элемент можно выбрать уже только n-1 способами. Третий - n-2 способами (т.к. 2 элемента уже выбраны). И так далее, k-й элемент можно выбрать n-(k-1) способами, предпоследний – двумя способами, а последний элемент – только одним способом, так как все остальные элементы так или иначе уже выбраны.
Что ж, теперь конструируем формулу.
Итак, число способов выбрать первый элемент из набора равно n. На каждый из этих n способов приходится по n-1 способу выбрать второй. Это значит, что общее число способов выбрать 1-й и 2-й элементы, в соответствии с правилом произведения, будет равно n(n-1). Далее, на каждый из них, в свою очередь, приходится по n-2 способа выбрать третий элемент. Значит, три элемента можно выбрать уже n(n-1)(n-2) способами. И так далее:
4 элемента -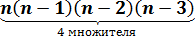 
способами,
k элементов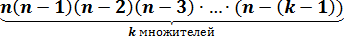 
способами,
n элементов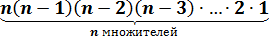 
способами.
Значит, n элементов можно выбрать (или в нашем случае расположить)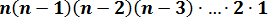 
способами.
Число таких способов обозначается так: Pn. Читается: «пэ из эн». От французского «P ermutation - перестановка». В переводе на русский означает: «перестановка из n элементов».
Значит,
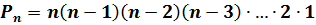
А теперь посмотрим на выражение 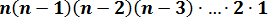, стоящее в правой части формулы. Ничего не напоминает? А если переписать справа налево, вот так?
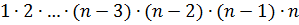
Ну, конечно! Факториал, собственной персоной. Теперь можно кратко записать:
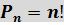
Значит, число всех возможных перестановок из n различных элементов равно n!.
В этом и состоит основной практический смысл факториала.
Решим задачи: