Свойства неопределённого интеграла
Нумеровать крайне не люблю, но здесь лучшего варианта не видно:
1) Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
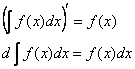
Доказательство: по определению неопределённого интеграла: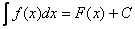 
, следовательно:
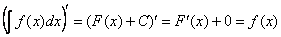, что и требовалось доказать.
Второе. По правилу раскрытия дифференциала (а точнее, по определению дифференциала) и только что доказанному пункту:
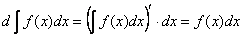
Слайд
2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
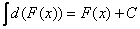
Учитывая, что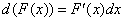 
, свойство можно переписать в следующем виде:
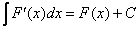
Тут даже доказывать ничего не надо, поскольку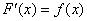 
и получается непосредственно само определение неопределённого интеграла.
Как видите, в обоих случаях значки дифференциала и интеграла взаимно уничтожаются, что естественно.
Следующие свойства вам хорошо знакомы – это мировые свойства линейности, которые справедливы и для других типов интегралов: определённых, двойных, тройных, криволинейных и пр.
Слайд
Константу можно вынести из-под знака интеграла
То есть, если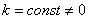 
, то 
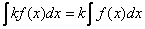
Доказательство: а вы как думали? =)
Найдём производную левой части. Используем свойство № 1:
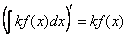
Найдём производную правой части. Используем правило дифференцирования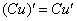 
и свойство № 1:
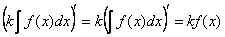
Получены одинаковые результаты, из чего и следует справедливость данного свойства.
Вообще, многие доказательства не столько сложны, сколько занудны и формальны – используются определения, ранее доказанные свойства, теоремы и т.д. Но, несмотря на их сухость, немалая часть студентов входит во вкус и даже начинает читать учебники по высшей математике в любой свободный момент.
4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
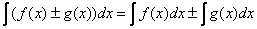
Справедливо для любого количества слагаемых.
Свойство проверяется точно так же, как и предыдущее – берутся производные от обеих частей.
7 слайд
Таблица интегралов
8 слайд
Перейдём к ещё более интересному разделу:
Определённые интегралы
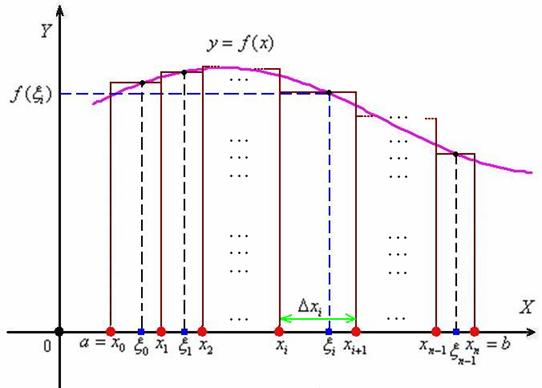
9 слайд
В результате получено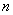 
частичных промежутков 
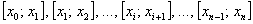с длинами 
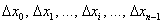соответственно. В общем случае длины различны – какие-то отрезки короче, какие-то длиннее. Максимальную длину называют диаметром разбиения и обозначают буквой «лямбда»: 
.
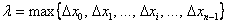Примечание: последняя запись читается, как «максимальное значение из множества (набора)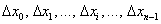 
»
В каждом из полученных промежутков опять же произвольно выбираем точки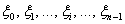 
(синие квадратики).
Примечание: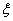 
(«кси») – 14-я буква греческого алфавита
Рассмотрим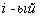 
промежуток 
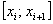. Его длина, очевидно, равна 
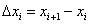(зелёная обоюдоострая линия). Значению аргумента 
соответствует значение функции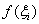 
(синие пунктирные линии), и произведение 
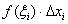в точности равно площади соответствующего коричневого прямоугольника.
Аналогично устроен каждый отрезок. Составим сумму, которая равна площади коричневой ступенчатой фигуры:
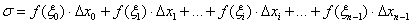
Данная сумма называется интегральной суммой, и её часто записывают в свёрнутом виде:
Что означает прилагательное «интегральной»? В широком смысле слова, интегрировать – это значит, что-то объединять. В данном случае интегральная сумма 
объединяет площади коричневых прямоугольников и с некоторой точностью приближает площадь криволинейной трапеции: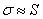 
Теперь зададимся вопросом: как улучшить точность приближения? Действия очевидны – увеличиваем и увеличиваем значение 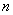. При этом количество отрезков 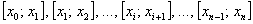растёт, а их длины 
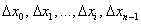– уменьшаются, в том числе неизбежно уменьшается и максимальная длина 
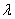. Количество точек 
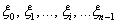тоже возрастает и ступенчатая фигура всё больше и больше напоминает криволинейную трапецию.
И, если количество отрезков разбиения устремить к бесконечности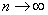 
, то интегральная сумма (площадь ступенчатой фигуры) будет стремиться к площади криволинейной трапеции: 
.
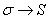Таким образом, площадь криволинейной трапеции равна пределу интегральной суммы при диаметре разбиения, стремящемся к нулю:
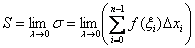
Наблюдаем за удивительным превращением:
1) В рассматриваемом контексте сумму 
ещё с 17 века обозначали растянутой буквой S (Summa). Это обозначение известно как значок интеграла:
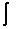
2) Если 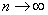(и, следовательно, 
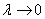), то значения 
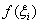стремятся «покрыть» все значения функции 
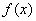из промежутка 
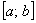, то есть:
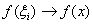, при этом пределы интегрирования: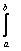 
3) И, наконец, длина любого промежуточного отрезка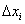 
становится бесконечно малой. Обозначение этой бесконечно малой длины мы тоже хорошо знаем, оно указывает, что объединение ведётся по переменной «икс»:
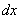
В результате, площадь криволинейной трапеции: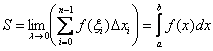 
Определение: конечный предел интегральной суммы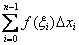 
при 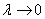, не зависящий ни от способа дробления отрезка 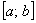, ни от выбора точек , называется определённым интегралом функции 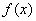по промежутку 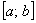и обозначается символом 
.
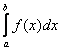При этом функция 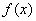называется интегрируемой в промежутке 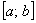. Для интегрируемости (а, значит, существования конечной площади), напоминаю, достаточно непрерывности функции на отрезке 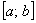. Если же на данном промежутке есть участки, где функция, например, не определена (нет её графика), то конечного предела 
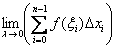и, соответственно, определённого интеграла 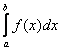не существует.