Доминирование стратегий в матричных антагонистических играх.

Игра с седловой точкой

В теории игр седловая точка (седловой элемент) — это наибольший элемент столбца матрицы игры, который одновременно является наименьшим элементом соответствующей строки (в игре двух лиц с нулевой суммой). В этой точке, следовательно, максимин одного игрока равен минимаксу другого; С. т. есть точка равновесия.

Рассмотрим некоторую игру 3´3, платёжная матрица которой дана табл. 5. Здесь как максиминный, так и минимаксный выигрыши равны 4. Иными словами, в данной игре нижняя и верхняя цена игры совпадают, обе равны 4. Выигрыш 4 является одновременно и максимальным из минимальных выигрышей для стратегий А₁, А₂, А₃ и минимальным из максимальных выигрышей для стратегий В₁, В₂, В₃. В геометрии точку на поверхности, являющуюся одновременно минимумом по одной оси координат и максимумом по другой, называют седловой точкой (см. рис. 1). По аналогии с геометрией элемент а₂₂=4 рассматриваемой здесь платёжной матрицы называют седловой точкой матрицы, а об игре говорят, что она имеет седловую точку.

Рис. 1. Пример поверхности с седловой точки

Достаточно посмотреть внимательно на матрицу (см. табл. 5), чтобы понять, что каждый из игроков должен придерживаться максиминной (минимаксной) стратегии. Эти стратегии являются оптимальными в игре с седловой точкой. Любое отклонение от них будет невыгодно для игрока, допустившего отклонение.

Если же игра не имеет седловой точки (см. табл. 4), то ни одна из стратегий Аi или Вi не является оптимальной.

Табл. 5. Платёжная матрица с седловой точкой

B A	В₁	В₂	В₃	Минимумы строк, a_i
А₁	2	3	7	2
А₂	5	4	6	4
А₃	6	2	1	1
Максимумы столбцов, b_j	6	4	7

Как быть, если игра не имеет седловой точки? Если каждый игрок вынужден выбирать одну-единственную чистую стратегию, то делать нечего: надо руководствоваться принципом минимакса. Другое дело, если можно свои стратегии "смешивать", чередовать случайным образом с какими-то вероятностями. Применение смешанных стратегий мыслится таким образом: игра повторяется много раз; перед каждой партией игры, когда игроку предоставляется личный ход, он "передоверяет" свой выбор случайности, "бросает жребий", и берёт ту стратегию, которая выпала.

Смешанные стратегии в теории игр представляют модель изменчивой, гибкой тактики, когда ни один из игроков не знает, как поведёт себя противник в данной партии. Такая тактика (правда, обычно безо всяких математических обоснований) часто применяется в карточных игра

12) Равновесие по Нэшу.

НЕЭШ- это известный американский математик.

есть другие принципы поиска равновесия или оптимального поведения игроков кроме максиминных и минимаксных. Ситуация от которой ни 1 из игроков в одиночку не выгодно отклонятся от группы называется равновесной по Нэшу.

выгодно или не выгодно менять столбец.

Для антагонистических игр 2 х лиц, принцип равновесия по Нэшу эквивалентен принципам минимакса и максимина и поиск равновесия сводится к поиску Седловых точек.

Если игра не антагонистическая, или чисто участников больше двух, то 1) Нэш доказал, что каждая такая игра имеет точку равновесия по Нэшу. и 2) что стратегия равновесия как правило не совпадает с со стратегиями максимина и минимакса, т.к. связаны с большем риском и требует смелости.

Произвольная игра в стратегической форме может не иметь ни одного равновесия Нэша, в котором каждый игрок выбирает (детермини- рованно) одну из своих чистых стратегий. Однако, чтобы достичь равновесия в игре, игроки могут случайным образом чередовать свои чистые стратегии, выбирая их с определенными вероятностями. Такого рода рандомизация (от англ. random – случайный) игроком своего выбора называется смешанной стратегией. С формально- математической точки зрения смешанная

стратегия представляет собой арифметический вектор – набор вероятностей, с которыми выбираются чистые стратегии игрока. Профиль, состоящий из смешанных стратегий, называется равновесием в смешанных стратегиях (или, для краткости, смешанным равновесием), если никакой игрок не может увеличить свой средний выигрыш (по сравнению с этим профилем), изменяя стратегию в одиночку. Нэш показал в 1951 году, что любая конечная игра в стратегической форме имеет смешанное равновесие.

Теорема Нэша. В каждой бескоалиционной игре существует хотя бы одна ситуация равновесия в классе смешанных стратегий.

Если, кроме того, функции Н_i(х) выпуклые вверх, то решение по Нэшу достигается в классе чистых стратегий.

Заметим, что принципиальная важность теоремы Нэша ограничивается существованием ситуации равновесия. Непосредственно применять ее для нахождения таких ситуаций не удается.

Дж. Нэшем была доказана также следующая теорема.

Теорема 2. Конечная бескоалиционная игра имеет симметричные ситуации равновесия, в которых игроки, равноправно входящие в игру согласно ее условиям, фактически оказываются в одинаковом положении.

Ее применение позволяет избежать отдельных ошибок при решении конечных бескоалиционных игр.

Одним из простых классов бескоалиционных игр ход решения которых поддается элементарному описанию являются биматричные игры, представляющие собой бескоалиционную игру двух игроков с ненулевой суммой.

Допустим, — игра n лиц в нормальной форме, где — набор чистых стратегий, а — набор выигрышей. Когда каждый игрок выбирает стратегию в профиле стратегий , игрок получает выигрыш . Заметьте, что выигрыш зависит от всего профиля стратегий: не только от стратегии, выбранной самим игроком , но и от чужих стратегий. Профиль стратегий является равновесием по Нэшу, если изменение своей стратегии с на не выгодно ни одному игроку , то есть для любого

Игра может иметь равновесие Нэша в чистых стратегиях или в смешанных (то есть при выборе чистой стратегии стохастически с фиксированной частотой). Нэш доказал, что если разрешить смешанные стратегии, тогда в каждой игре n игроков будет хотя бы одно равновесие Нэша.

13) Смешанные стратегии в матричных антагонистических играх. Доминирование стратегий в матричных антагонистических играх.

В рассмотренных выше играх, каждый игрок применяет в игре только одну из своих возможных стратегий, это строки или столбцы матрицы. Если такая игра не имеет решений в чистых стратегиях, то есть отсутствует Седлова точка. То оказывается, что игрокам разумно действовать случайно, чтобы обеспечить наибольшую скрытность в выборе стратегии. Результат случайного выбора не может стать известным противнику поскольку до реализации самого выбора не известен самому игроку. если игрок знает или догадывается как поступит другой, то надо поступить так чтобы другой проиграл. случайность выбора должна быть. решение таких игр находится уже не в чистых, а так называемых смешанных стратегиях, которые являются наилучшей в том смысле, что позволяет первому игроку действовать лучшим образом для максимизации своего выигрыша, а второму игроку для минимизации своего проигрыша. Фон Неймон доказал, что любая игра двух лиц с нулевой суммой- антагонистическая, имеет решение в оптимально смешанных стратегиях, т.е. в чистых она не имела решения. Чистые стратегии можно представить в виде

х= (х1,.....,хм)- вектор для первого, который контролирует строки матрицы. компоненты этого вектора представляют собой вероятности использования в игре первым игроком соответствующих чистых стратегий(строк матрицы) при этом сумма хi=1<-xi<-1

у=(у1,..........,ун) то вектор второго игрока, который контролирует столбцы матрицы и компоненты которого представляют собой вероятности использования вторым игроком дитого столбца матрицы, так де сумма yi=1,0<-y<-1

решение для игры дуэли:

x*=y*=(0,5/11,5/11,5/11,0,1/11)

это шаги дуэли.2 и 3 шаг дают наибольшую эффективность.

другой пример.

магазин может завести товар 5 типов, если товар будет пользоваться спросом, то он получает прибыль от реализации, если не будет пользоваться, то в убыток, товары считаются такими, что спрос на один из них означает отсутствие спроса на другой. 1 игрок это магазин, а 2 игрок это покупательский спрос.

тип товара - т.т. Д-доход, У - убыток.

т.т. Д У

1 32 16

2 32 8

3 32 4

4 32 4

5 32 2 спрос

платежная матрица, имеет такой вид

32 -16 -16 -16 -16

-8 32 -8 -8 -8

-4 -4 32 -4 -4

-4 -4 -4 32 -4

-2 -2 -2 -2 32

оптимальное решение x*=(0,16;0;19;0;21;0:21;0:23)

Существуют способы позволяющие точно находить оптимальные смешанные стратегии. эти способы достаточно сложны и трудоемки и поэтому мы рассмотрим простой случай, когда платежная матрица имеет размерность 2*2. В этом случае оптимальные и смешанные стратегии определяются так, чтобы игрок 1 получил одинаковый выигрыш для каждого столбца соответствующего чистой стратегии игрока 2, аналогично игрок 2 должен прировнять платеж по обеим строкам.

пример: пусть платежная матрица имеет вид

1 2

3 0

решить эту игру, начинаем с решения чистых стратегий.

по строкам. мин. 1 и 0 макс. 1.

по столбцам 3 и 2 мин-2.

2 не равно 1. игра не имеет чистых стратегий.

далее,

1 2

3 0

написано в тетради стр 1.

Х это вероятность того, что 1 игрок выберет 1 стратегию.

у это вероятность что 1 игрок выберет 2 столбец

Первый игрок получает одинаковый выигрыш для каждого столбца.

Если 2 игрок выберет 1 столбец, то выигрыш 1 игрока составит х+3(1-х)

А если 2 выберет 2 столбец, то выигрыш первого 2х+ 0 (1-х) и это нужно приравнять к х+3(1-х)

то 3(1-х)= х

3-3х=х

х= 3/4.

оптимальная х*=(3/4, 1/4)х

теперь выигрыш 2 игрока не должен завесить от того, какую строку выберет 1 игрок. поэтому приравняем выигрыш 2 игрока по 1 и по 2 строке матрицы.

если 1 игрок выберет 1 строку, то выигрыш составит у+2(1-у) и прировнять к выигрышу 2 если 1 игрок выберет 2 строку = 3у+0(1-у)

2(1-у)=2у

1-у=у, у= 1/2.

и поэтому оптимальная стратегия 2 игрока будет у*=(1/2;1/2), т.е. он с равной вероятностью выбирает столбцы матрицы.

Ожидаемый выигрыш первого игрока составит х+3(1-х) или тоже самое 2х+0(1-х)

v= 2*3/4=6/4=1,5.

Ожидаемый проигрыш 2 игрока 3 у+0(1-у) че то там 1,5. они должны совпадать. игра если антагонистическая, то проигрыш олного это сумма выигрыша другого.

Доминирование стратегий в матричных антагонистических играх.

понятие доминирования позволяет при нахождении оптимальных стратегий игроков уменьшить размерность платежной матрицы. Доминируемой, является такая строка, каждый элемент которой не превышает соответствующий элемент другой строки.

5 7

1 2

1 тут никогда не выберет номинируемую строку, т,е. вероятность ее выбора будет равно нулю.

Доминирующим называется столбец, каждый элемент которого превышает соответствующий элемента другого столбца. 2 игрок тут никогда не выберет доминирующую стратегию. Поэтому общий алгоритм решения матричных игр двух лиц. В начале ищется решение в чистых стратегиях, т,е. Седловой точки Если Седловой точки нет, то далее отбрасываются все доминируемые строки и доминирующие столбцы, после этого ищется решение в смешанных стратегиях.

Пример:

в тетради. записано под (2ж) матрица 4*4.

2110 0

2313 1

3020 0 макс-1

0300 0

3326 мин-2

ищем Седлову. точку, ее нет, задание не имеет решение в чистых стратегиях

вычеркиваем, чтобы упростить, 1 столбец и строчку и 4 строчку, квадратом.

осталось у нас

у 1-у

х 31

1-х 02

в тетради, решение:

х*=(0;1/2;1/2;0)

у*=(0;1/4;3/4;0)

ИЗ ИНЕТА!

Определение. Случайная величина, значениями которой являются чистые стратегии игрока, называется его смешанной стратегией.

Таким образом, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его чистые стратегии.

Будем обозначать смешанные стратегии игроков А и В соответственно

S_A=||p₁, p₂,..., p_m||,

S_B=||q₁, q₂,..., q_n||,

где p_i - вероятность применения игроком А чистой стратегии А _і; ;

q_j - вероятность применения игроком В чистой стратегии B_j; .

В частном случае, когда все вероятности, кроме одной, равны нулю, а эта одна - единице, смешанная стратегия превращается в чистую.

Применение смешанных стратегий осуществляется, например, таким образом: игра повторяется много раз, но в каждой партии игрок применяет различные чистые стратегии с относительными частотами их применения, равными p _i и q _j.

Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, какую чистую стратегию выберет противник в данной партии.

Если игрок А применяет смешанную стратегию S_A=||p₁, p₂,..., p_m||, а игрок В смешанную стратегию S_B=||q₁, q₂,..., q_n||, то средний выигрыш (математическое ожидание) игрока А определяется соотношением

. (2.6)

Естественно, что ожидаемый проигрыш игрока В равен такой же величине.

Итак, если матричная игра не имеет седловой точки, то игрок должен использовать оптимальную смешанную стратегию, которая обеспечит максимальный выигрыш n.

14) Понятие и поиск оптимальных смешанных стратегий в матричных антагонистических играх.

Смешанная стратегия игрока - это полный набор применения его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. игра без седловой точки;

• игроки используют случайную смесь чистых стратегий с заданными вероятностями;

• игра многократно повторяется в сходных условиях;

• при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком;

• допускается осреднение результатов игр.

Применяются следующие обозначения смешанных стратегий.

Для игрока 1 смешанная стратегия, заключающаяся в применении чистых стратегий А₁, А₂,..., А_m с соответствующими вероятностями р₁, р₂,..., р_m,

Антагонистическиеигры (матем.), понятие теории игр (см. Игр теория). А. и. — игры, в которых участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для А. и. характерно, что выигрыш одного игрока равен проигрышу другого и наоборот, поэтому совместные действия игроков, их переговоры и соглашения лишены смысла. Большинство азартных и спортивных игр с двумя участниками (командами) можно рассматривать как А. и. Принятие решений в условиях неопределённости, в том числе принятие статистических решений, также можно интерпретировать как А. и. Определяются А. и. заданием множеств стратегий игроков и выигрышей игрока I в каждой ситуации, состоящей в выборе игроками своих стратегий. Таким образом, формально А. и. есть тройка ‹ А, В, Н›, в которой А и В — множества стратегий игроков, а Н (а, b) — вещественная функция (функция выигрыша) от пар (а, b), где а Î A, b Î В. Игрок I, выбирая а, стремится максимизировать Н (а, b),а игрок II, выбирая b, — минимизировать Н (а, b). А. и. с конечными множествами стратегий игроков называются матричными играми.

Основой целесообразного поведения игроков в А. и. считается принцип минимакса. Следуя ему, I гарантирует себе выигрыш

точно так же II может не дать I больше, чем

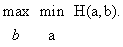
Если эти "минимаксы" равны, то их общее значение называется значением игры, а стратегии, на которых достигаются внешние экстремумы, — оптимальными стратегиями игроков. Если "минимаксы" различны, то игрокам следует применять смешанные стратегии, т. е. выбирать свои первоначальные ("чистые") стратегии случайным образом с определёнными вероятностями. В этом случае значение функции выигрыша становится случайной величиной, а её математическое ожидание принимается за выигрыш игрока I (соответственно, за проигрыш II).

Существуют способы позволяющие точно находить оптимальные смешанные стратегии. Эти способы достаточно сложны и трудоемки и поэтому мы рассмотрим простой случай, когда платежная матрица имеет размерность 2*2. В этом случае оптимальные и смешанные стратегии определяются так, чтобы игрок 1 получил одинаковый выигрыш для каждого столбца соответствующего чистой стратегии игрока 2, аналогично игрок 2 должен прировнять платеж по обеем строкам.

пример: пусть платежная матрица имеет вид

1 2

3 0

решить эту игру, начинаем с решения чистых стратегий.

по строкам. мин. 1 и 0 макс. 1.

по столбцам 3 и 2 мин-2.

2 не равно 1. игра не имеет чистых стратегий.

далее,

1 2

3 0

написано в тетради стр 1.

Х это вероятность того, что 1 игрок выберет 1 стратегию.

у это вероятность что 1 игрок выберет 2 столбец

Первый игрок получает одинаковый выигрыш для каждого столбца.

Если 2 игрок выберет 1 столбец, то выигрыш 1 игрока составит х+3(1-х)

А если 2 выберет 2 столбец, то выигрыш первого 2х+ 0 (1-х) и это нужно приравнять к х+3(1-х)

то 3(1-х)= х

3-3х=х

х= 3/4.

оптимальная х*=(3/4, 1/4)х

теперь выигрыш 2 игрока не должен зависеть от того, какую строку выберет 1 игрок. поэтому приравняем выигрыш 2 игрока по 1 и по 2 строке матрицы.

2(1-у)=2у

1-у=у, у= 1/2.

Ожидаемый выигрыш первого игрока составит х+3(1-х) или тоже самое 2х+0(1-х)

v= 2*3/4=6/4=1,5.

Ожидаемый проигрыш 2 игрока 3 у+0(1-у) че то там 1,5. они должны совпадать. игра если антагонистическая, то проигрыш одного это сумма выигрыша другого.

15) Понятие биматричных неантагонистических игр. Примеры таких игр.

Игры с ненулевой суммой. антагонистические суммы.

однако реальные конфликты далеко не исчерпываются только антагонистическими ситуациями, часто интересы сторон противоречат друг другу, но не являются противоположными.

рассмотрим наиболее простые игры с не противоположными интересами в которых учувствуют два лица, а множество их стратегий конечно- биматричные игры. выигрыш игроков можно записать в виде двух матриц- 1 матрица выигрыш 1 игрока, 2 матрица- это матрица выигрыш второго игрока.

записи на листочке от 18.11.2013.

Часто эти 2 матрицы объединяются в 1 матрицу, которые имеют вид: в тетради. биматрица. би- то есть из двух.

Математической моделью конфликтов с двумя участниками являются биматричные игры. Такая игра 2х2 задается биматрицей (a_ij,b_ij). В кооперативном варианте такой игры игроки могут согласованно выбирать элемент биматрицы. Если они выбрали элемент (a,b), то Первый игрок получает a, а Второй получает b. Цели игроков одинаковы - выиграть как можно больше в расчете на партию в среднем. Пусть (x,y), (a,b) - две точки из CE. Говорят, что (x,y) доминирует (a,b) если x≥a, y≥b и хотя бы одно из этих неравенств строгое. Недоминируемые точки называются оптимальными по Парето, а их множество - множеством оптимальности по Парето. Еще более узкое множество называется переговорным. Оно определяется так: пусть V_k - максимальный выигрыш, который k-й игрок может обеспечить себе при любой стратегии другого игрока, тогда переговорное множество определяется как множество тех точек множества Парето, у которых k-я координата не меньше V_k. Для нахождения V_k на до решить две задачи ЛП:

V₁→max, a₁₁*x+a₂₁*(1-x) ≥V₁,a₁₁*x+a₁₂*(1-x)≥V₁, 0≤x≤1;

V₂→max, a₁₁*y+a₁₂*(1-y) ≥V₂,a₂₁*y+a₂₂*(1-y)≥V₂, 0≤y≤1.

Пример 1. Игра “Семейный спор”
Одна из наиболее распространенных интерпретаций игры следующая. Муж (первый игрок) и жена (второй игрок) могут выбрать одно из двух вечерних развлечений: футбольный матч или балет. Естественно предположить, что муж предпочтет футбол, а жена – балет. Однако для обоих гораздо важнее идти вместе, чем смотреть предпочитаемое зрелище в одиночестве. В данной 2х2 биматричной игре функции выигрышей Н₁ и Н₂ соответственного первого и второго игроков можно представить в виде
и ,
где стратегии игрока 1: А₁ – выбираю футбол; А₂ – иду на балет; игрока 2: В₁ – иду на футбол, В₂ – на балет.
Очеви дно, что для первого игрока предпочтительнее ситуация (А₁, В₁), а для второго (А₂, В₂), и эти ситуации являются равновесными. Однако в данном примере как будет показано ниже, есть еще и третья ситуация равновесия, состоящая в выборе игроками смешанных стратегий:; с ценой игры для обоих игроков .
Однако выигрыши каждого из игроков в этой ситуации равновесия меньше, чем в двух первых ситуациях равновесия, где они равны 2 или 1, в зависимости от ситуации и игрока.
Хотя стратегии (А₁,В₁) и (А₂,В₂) являются оптимальными, поскольку дают максимальные выигрыши, однако приносят игрокам не одинаковые выигрыши, поэтому не являются справедливыми.
Отметим также, что если в матричной игре ни одному из игроков не выгодно информировать противника о своей стратегии, то в данной биматричной игре это свойство не выполняется.
Действительно, если игроки не общаются до игры и оба обладают твердыми характерами, т.е. первый игрок выбирает стратегию А₁, а второй – В₂, то в результате они оба проигрывают. Аналогичная ситуация получиться и в том случае, когда каждый из игроков имеет мягкий характер и решает уступить.Так сочетание устойчивости со справедливостью вступает в противоречие с сочетанием устойчивости и выгодности.
Лучшим для игроков в рассматриваемой игре является договорный вариант (А₁,В₁) или (А₂,В₂), причем справедливым решением будет их выбор одного из этих вариантов путем бросания монеты. Выпадение герба будет означать, например, что семейство идет на матч по футболу, а решки – на балет. Заметим, что в антагонистической игре в отличие от биматричной нет смысла вести переговоры до игры и уславливаться о совместном плане действий. В рассматриваемой игре, ясно, что если игроки договорились бы играть оба, скажем первую чистую стратегию, причем игрок 1 за получение большего выигрыша, чем игрок 2, заплатил бы ему 1/2, то решение было бы выгодным и справедливым для обоих игроков. Однако в рамках бескоалиционных игр такого рода дележи не предусматриваются.

16) Оптимальность по Парето. Примеры Парето- оптимальных и не оптимальный стратегий матричных неантагонистических играх.

ситуация оптимальна по Парето, если невозможно улучшение выигрыша хотя бы одного игрока, не ухудшая выигрыш других.

содержательная позиция по нешу и ситуация оптимальная по Парето сводится к следующему. в 1 ситуации ни 1 игрок действуя в одиночку не может увеличить своего выигрыша, во второй все игроки действуя совместно не могут увеличить выигрыш каждого.

толпа людей наблюдает какое то зрелище, кому плохо видео- он встает на цыпочки, тогда он мешает следующим, это приедет к тому, что все встанут на цепочки.

Оптимальность по Парето — такое состояние системы, при котором значение каждого частного критерия, описывающего состояние системы, не может быть улучшено без ухудшения положения других элементов.

Другой вариант устойчивости ситуации в большей степени, чем равновесность, отражающей черты ее выгодности, состоит в ее оптимальности по Парето[1].

Определение 6. Ситуация х ₀ в бескоалиционной игре называется оптимальной по Парето, если не существует ситуации х ÎC, для которой имеет место векторное неравенство

, для всех іÎІ. (5.2)

Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш кого-либо из них, не уменьшив при этом выигрыш кого-либо другого.

Подчеркнем различие ситуации равновесия от ситуации, оптимальной по Парето: в первой ни один игрок, действуя в одиночку, не может увеличить свой собственный выигрыш; во второй, – все игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого.

Вопросы об оптимальных по Парето ситуациях решаются в принципе проще, чем аналогичные вопросы о ситуациях равновесия (оптимальных по Нэшу).

Проиллюстрируем графический метод определения ситуаций оптимальных по Парето. На рис. 5.1 изображено множество возможных стратегий х ₁, х ₂ двух игроков. Каждой точке х ÎC соответствует точка на множестве Н значений функций выигрышей Н₁(х) и Н₂(х) (рис. 5.2).

Рис. 5.1 Рис. 5.2

На рис. 5.2 дуга АСВ соответствует множеству ситуаций оптимальных по Парето, так как никакими совместными усилиями игроков, нельзя увеличить выигрыш одного из них, не уменьшив при этом выигрыш другого.

17) Равновесие по Нэшу в неантагонистических играх. Определение и примеры.

НЕЭШ- это известный американский математик.

выгодно или не выгодно менять столбец.

Антагонистическая игра когда она взаимно исключаемая получается т.е. выигрыш 2 и -2

а не антагонистическая наоборот. там будут не противоположные интересы.

Если, кроме того, функции Н_i(х) выпуклые вверх, то решение по Нэшу достигается в классе чистых стратегий.

Доминирование стратегий в матричных антагонистических играх.

Поиск по сайту