Вычисление двойного интеграла в декартовых координатах
Пример 1. Вычислить интеграл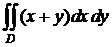 
, где область 
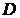ограничена прямыми 
.
Решение. Прямоугольная область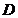 
задается неравенствами 
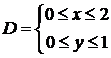, она простая в любом направлении. Перейдем от двойного интеграла к повторному по:
.
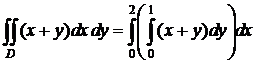Вычислим сначала внутренний интеграл:
.
Осталось вычислить внешний интеграл
.
Изменим порядок интегрирования
.
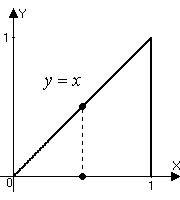
Теперь внутренний интеграл: 
,
Внешний: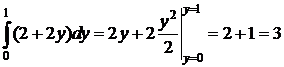 
.☻
Пример 2. Вычислить интеграл 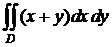, где область 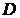ограничена линиями 
.
Решение. Область 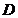можно задать неравенствами 
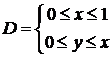. Область размещена в вертикальной полосе 
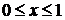, снизу ограничена линией 
, сверху – линией 
, т.е.она 
простая. Запишем: 
.
Внутренний интеграл: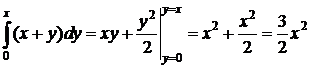 
,
Внешний: 
Эту же область можно задать другой системой неравенств: 
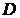. Теперь область размещена в горизонтальной полосе 
, слева ограничена линией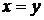 
, справа – линией 
, т.е.она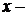 
простая.Запишем:
.
Внутренний интеграл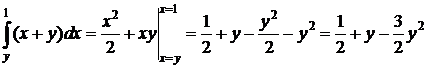 
Внешний: 
☻
Пример 3. Вычислить интеграл 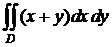, где область 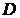ограничена линиями 
, , 
;.
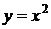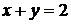Решение. Область 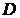зададим неравенствами 
. Эта область размещена в горизонтальной полосе , слева ограничена линией 
, справа – линией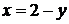 
, т.е. область 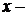простая.Запишем:
.
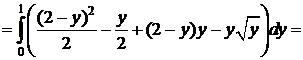
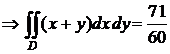Попробуем для этой области изменить порядок интегрирования. Если поместить область в вертикальную полосу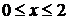 
, то нижняя граница – линия , а верхняя граница составлена из двух линий, параболы 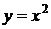и прямой 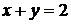. Поэтому в направлении оси 
область не является правильной. Разобьем область 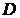прямой на части 
и 
: 
, 
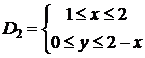. Области и являются простыми. Двойной интеграл представим в виде суммы двух интегралов:
.
.
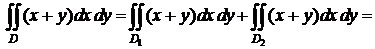
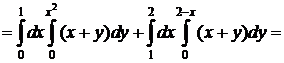
Мы видим, что для этого интеграла меньше вычислений оказалось при первом выборе порядка интегрирования. ☻
Замена переменных в двойном интеграле.
Вычисление двойного интеграла в полярных координатах
Пример 1. Вычислить интеграл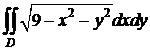 
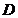, – круг 
.
Решение. В заданном круге полярный радиус 
изменяется от 
до 
; полярный угол изменяется от 
до 
. Перейдем к полярным координатам, тогда подынтегральная функция примет вид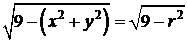 
. Запишем:
.
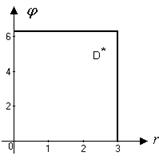
Область D в декартовой системе координат определяется неравенством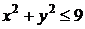 
, а в полярной системе координат – неравенствами 
, 
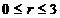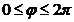. Область D– круг в плоскости 
– преобразуется в область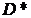 
– прямоугольник в плоскости 
. ☻
Приложения двойного интеграла
Пример 1. Найти объем тела, ограниченного поверхностями
.
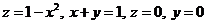Решение. Сверху тело ограничено поверхностью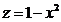 
– это параболический 
-цилиндр (его образующие параллельны оси ). С боков тело ограничено вертикальными плоскостями и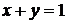 
. Снизу тело ограничивает плоскость 
. Область интегрирования – треугольник в плоскости , 
. По формуле (а) запишем:
.☻
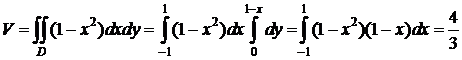Пример 2. Найти объем тела, ограниченного поверхностями 
и 
.
Решение. Параболоид вращения 
с вершиной в точке 
, 
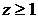ограничивает тело снизу. Второй параболоид вращения 
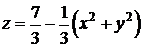с вершиной в точке 
, 
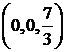ограничивает тело сверху. Решаем систему
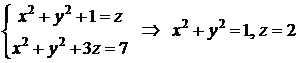
Получили уравнение линии пересечения параболоидов, она проектируется на плоскость в границу круга 
.
Найдём объем тела с основанием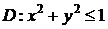 
и ограниченного сверху поверхностью 
:
.
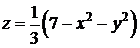Переходим к полярным координатам:
.
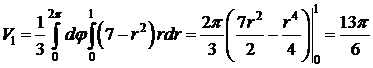Найдём объем тела с основанием 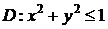и ограниченного сверху поверхностью 
:
.
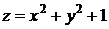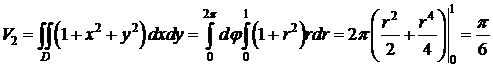Очевидно, объём тела равен разности найденных объёмов:
. ☻
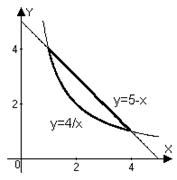
Пример 3. Найти площадь фигуры, ограниченной линиями
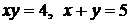
Решение. По формуле (б)
.
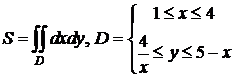Вычислим 
.
Такого типа задачи решали раньше с помощью определенного интеграла. ☻
Пример 4. Найти площадь эллипса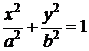 
.
Решение. Перейдем к обобщенным полярным координатам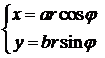 
. Найдем якобиан преобразования:
.
На эллипсе переменные 
изменяются в пределах 
, 
. По формуле (б) 
. Этот результат нам уже знаком. ☻
Пример5. Найти массу, статические моменты 
и координаты центра тяжести фигуры, лежащей в первой четверти и ограниченной эллипсом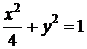 
и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
Решение: По условию, плотность 
, где 
– коэффициент пропорциональности. Область интегрирования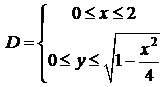 
. По формуле (г) находим массу пластинки: 
.
Находим статические моменты пластинки находим по формулам (д):
, 
.
Наконец, по формулам (е) находим координаты центра тяжести:
. и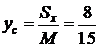 
.☻