ОТЧЕТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ №1
Дисциплина: Методы оптимизации
Тема: Решение задач линейного программирования
Выполнил студент гр. 33601/1 Д.О. Труфанов
Руководитель, доцент Е.А. Родионова
«___»________________2015 г.
Санкт-Петербург
Симплекс-метод решения задач линейного программирования
1. Постановка задачи.
Составить и решить задачу линейного программирования симплекс методом.
Построить и решить двойственную ей задачу симплекс методом.
В качестве опорного плана взять вектор, найденный методом искусственного базиса.
Предусмотреть возможность задания исходных данных с абсолютной погрешностью и указать погрешность результата.
Требования к составляемой задаче:
× 5 переменных
× 2 ограничения в виде равенства
× 2 ограничения в виде неравенства
× 3 переменных с ограничением на знак
Составим исследуемую задачу 1:






Для отдельного примера по решению, найденному симплекс методом для прямой задачи, восстановить решение двойственной задачи.
Задача 2:





2. Исследование применимости метода:
Метод применим к любой задаче линейного программирования, представленной в каноническом виде. Поскольку на данный момент задача (1) к каноническому виду не приведена, то приведём её к таковому.
Для этого, сначала, введём замену переменных:
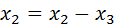

А также ведём дополнительные переменные, чтобы получить ограничения в виде равенств:
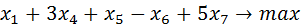





Для применимости к задаче симплекс-метода необходимо и достаточно, чтобы матрица A была полного ранга(rang(A) = min{ m, n }).
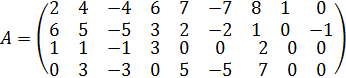
Ранг матрицы A равен 4, следовательно, это матрица полного ранга.
Приведем задачу (2) к виду, необходимому для симплекс-метода:


 1
1


Для применимости симплекс-метода проверим ранг матрицы A.

Ранг матрицы А равен 3, значит симплекс метод применим.
Построим двойственную к задаче (1).
Приведем задачу (1) к следующему виду для построения двойственной задачи:


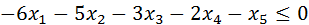



Двойственная задача будет иметь вид:







Приведем задачу к каноническому виду:



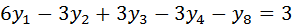



Также построим задачу, двойственную к задаче (2).






3. Описание алгоритма:
1) Алгоритм симплекс метода.
Рассмотрим один шаг алгоритма.
Пусть имеется  – опорный вектор.
– опорный вектор.
Построим опорный вектор  , для которого
, для которого



Столбцы матрицы  линейно независимы, так как
линейно независимы, так как  – опорный вектор.
– опорный вектор.
Пополним столбцы матрицы 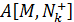 столбцами из
столбцами из  так чтобы матрица
так чтобы матрица  была квадратной(
была квадратной( ) и
) и  .
.
Обозначим 
Для построения алгоритма используем необходимые и достаточные условия оптимальности для канонической задачи линейного программирования.
 (1)
(1)
 (2)
(2)
Воспользуемся условием (2) и составим уравнение относительно 
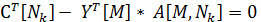 (3)
(3)
Так как
 ,
,
то (3) можно разрешить относительно  :
:
 ,
,
где
 .
.
Для построенного таким образом  условие (2) выполнится автоматически, так как
условие (2) выполнится автоматически, так как  .
.
Проверим выполнение условия (1).
Подставим  в (3) и результат разобьём на 2 вектора:
в (3) и результат разобьём на 2 вектора:


Рассмотрим вектор  :
:
если  , то
, то  - оптимальный, так как для него выполнены необходимые и достаточные условия оптимальности. Алгоритм заканчивается.
- оптимальный, так как для него выполнены необходимые и достаточные условия оптимальности. Алгоритм заканчивается.
Если  такое что
такое что 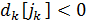 , то ищем следующий опорный вектор
, то ищем следующий опорный вектор  .
.
Строим вектор
 ,
,
 ,
, 
И с его помощью получаем вектор

Рассмотрим вопрос выбора θ.
Если  то, так как
то, так как  ,
,  , можно
, можно  , следовательно
, следовательно  .
.
В этом случае алгоритм симплекс метода заканчивается: показано, что функция не ограничена снизу на множестве допустимых значений.
Если  такое, что
такое, что  , то θ ограничено сверху условием
, то θ ограничено сверху условием
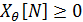 .
.
Пусть  невырожденный опорный вектор, тогда
невырожденный опорный вектор, тогда
 .
.
Тогда можно найти 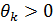 :
:
 ,
,
 ,
,
 .
.
Пусть  вырожденный опорный вектор, и
вырожденный опорный вектор, и
 .
.
Тогда можно найти 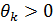 :
:
 ,
,
 ,
,
 .
.
Если  такое, что
такое, что  , то нельзя найти
, то нельзя найти 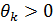 , для продолжения алгоритма требуется изменить базис вектора
, для продолжения алгоритма требуется изменить базис вектора  .
.
Следует выбрать столбец  ,
,  и заменить вектором
и заменить вектором  ,
,  .
.
Проверим, является ли новая система векторов линейно независимой.
Если система векторов линейно зависима, то следует менять столбцы до тех пор, пока не получится линейно независимая система.
Если система векторов линейно независима, то происходит возврат к началу алгоритма.
Для совершения хотя бы первого шага алгоритма необходимо иметь первый опорный вектор. Найти его можно методом искусственного базиса
2) Алгоритм метода искусственного базиса.
Рассмотрим алгоритм построения начального опорного вектора методом искусственного базиса.
Рассмотрим вспомогательную каноническую задачу линейного программирования.



Считаем, что 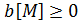
В противном случае можно левую и правую часть уравнения, в котором коэффициент меньше 0, умножить на -1.
Для такой задачи опорный вектор легко найти:
 ,
,
так как множество допустимых точек не пусто, и функция цели ограничена снизу, то можно использовать для неё алгоритм симплекс метода
Возможны 2 варианта решения вспомогательной задачи:
Если  такое, что
такое, что  , то исходная задача не имеет ни одной допустимой точки.
, то исходная задача не имеет ни одной допустимой точки.
В противном случае,  является опорным вектором исходной задачи.
является опорным вектором исходной задачи.
3) Алгоритм восстановления решения двойственной по решению прямой.
Пусть известно некоторое решение прямой задачи линейного программирования 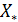 .
.
Для восстановления решения двойственной задачи рассмотрим ограничения исходной задачи, в которых при подстановке 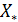 получается строгое неравенство.
получается строгое неравенство.
Тогда из условий дополняющей нежесткости получим, что соответствующие  могут быть равны только нулю. Кроме этого, ограничения двойственной задачи, соответствующие переменным произвольного знака прямой задачи, по тем же условиям обращаются в равенство, и значение функции цели двойственной задачи на оптимальном решении должно совпадать со значением функции цели на
могут быть равны только нулю. Кроме этого, ограничения двойственной задачи, соответствующие переменным произвольного знака прямой задачи, по тем же условиям обращаются в равенство, и значение функции цели двойственной задачи на оптимальном решении должно совпадать со значением функции цели на 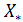 .
.
Таким образом, для получения решения двойственной задачи достаточно решить систему линейных уравнений, составленную из описанных соотношений.
4. Результаты работы метода:
Результат решения прямой задачи (1) симплекс методом:

Значение функции цели: 142
Достоверность полученных результатов следует из условий оптимальности (1) и (2).
 (1)
(1)
 (2)
(2)
(1): 
(2): 
Результат решения двойственной задачи симплекс методом:

Значение функции цели: 142
Достоверность полученных результатов следует из аналогичных условий оптимальности и из равенства значений функций цели прямой задачи и двойственной.
Результат решения прямой задачи (2) симплекс методом:

Значение функции цели: -1.
Восстановленоe решение двойственной задачи:

Значение функции цели: -1.
Достоверность решения двойственной задачи, восстановленного по решению прямой, подтверждается допустимостью полученного решения и равенством значений функций цели прямой задачи и двойственной.
5. Анализ результатов работы метода:
Рассмотрим влияние внесения погрешности в параметры задачи.
1) При внесении погрешности в матрицу  :
:
Решение без погрешности:

| Eps | Решение | Значение |
| 0.1 | 
| 135.148 |
| 0.01 | 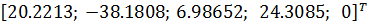
| 65.4893 |
| 0.001 | 
| 65.6216 |
2) При внесении погрешности в вектор ограничений:
| Eps | Решение | Значение |
| 0.1 | 
| 141.927 |
| 0.01 | 
| 141.993 |
| 0.001 | 
| 141.999 |
3) При внесении погрешности в функцию цели:
| Eps | Решение | Значение |
| 0.1 | 
| 143.312 |
| 0.01 | 
| 142.131 |
| 0.001 | 
| 142.013 |
При введении погрешности в коэффициенты матрицы ограничений задачи, результат сильно отличается от истинного решения. При внесении погрешности в коэффициенты функции цели изменяется только значение функции цели.