НЕЛИНЕЙНЫЕ СИСТЕМЫ С КОРРЕКЦИЕЙ

ЛЕКЦИЯ 28, 29. Линейная коррекция нелинейных систем.

План.

1. Точность функционирования и качество процессов около устойчивого состояния равновесия.

2. Нормированный коэффициент гармонической линеаризации,

В этой главе рассматривается задача синтеза нелинейных систем не в смысле оптимизации, а как задача введения в заданную систему дополнительных устройств (корректирующих) для удовлетворения предъявляемым к системе техническим требованиям.

Для достижения требуемой точности и качества процесса в нелинейные системы можно вводить линейные корректирующие устройства такие же, как и в линейных системах (см. [23]). Эти линейные корректирующие устройства могут быть последовательными (с введением производных, интегралов и т. п.) и параллельными (в виде местных обратных связей различного типа).

Рассмотрим системы с одной нечетно-симметричной однозначной нелинейностью F(х), гармоническая линеаризация которой имеет вид

F(x) =q(a) x, (7.1)

где коэффициент гармонической линеаризации принимает ограниченные значения

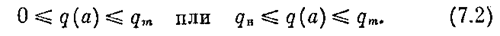
К такого типа нелинейностям относятся, например, нелинейности, изображенные на рис. 1.1, а, б, г, д, е и рис.1.2, б, в. Более сложные случаи рассматриваются в книге [19].

Случаи наличия нелинейностей вида рис. 1.2, а и рис. 1.5, а, когда коэффициент q (a) принимает бесконечное значение при а = 0, здесь не рассматриваются, так как в этих случаях невозможно обеспечить устойчивое равновесное состояние системы в нулевой точке и установившийся режим будет автоколебательным. В этих случаях путем введения линейных корректирующих устройств можно добиваться приемлемых значений параметров (а, w) автоколебаний. Но это следует делать с помощью методов расчета автоколебаний, изложенных выше. Здесь мы будем рассматривать точность и качество процессов около устойчивого равновесного состояния в нулевой точке.

Пусть схема системы имеет вид, изображенный на рис. 7.1. Положим, что линейное корректирующее уст­ройство любого типа вводится в одну из линейных частей,

Рис. 7.1.

т. е. в блок W1(s) или W2(s), не охватывая нели­нейного звена F(x). Условимся в формуле гармониче­ской линеаризации (7.1) записывать

где k — коэффициент усиления (его определение для различных нелинейностей показано на рис. 1.1). Тогда выражение q0(а) можно получить, согласно лекции 13, 14 в виде

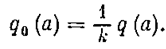
Например, для кубической нелинейности из (4.22) имеем

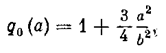
а для характеристики с насыщением (рис. 4.8, в), соглас­но (4.28), получаем

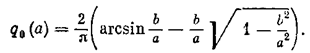
Указанный в формуле (7.3) коэффициент k будем относить к передаточной функции линейной части систе­мы, Так, для схемы рис, 7,1 передаточную функцию такой приведенной линейной части будем записывать в виде

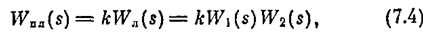
где k - коэффициент, выделенный из нелинейности согласно (7.3).

Соответственно в случае релейной характеристики (рис. 1.2, б) в качестве величины k примем значение qmax

В этом случае, согласно формулам (7.3), (7.5) и (4.23), получим

Величину q0(а) будем называть нор М ированны М коэффи­циенто М гар М онической линеаризации. Тогда синтез кор­ректирующего устройства можно производить следую­щим образом.

1. Строится логарифмическая амплитудная частотная характеристика первоначально заданной приведенной ли­нейной части системы:

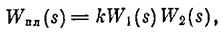
где k — коэффициент усиления, перенесенный из нели­нейности.

2. Формируется желаемая логарифмическая ампли­тудная частотная характеристика линейной части Wж(s)в соответствии с требованиями точности и качества про­цессов, как это изложено в теории линейных систем (см. [23]).

3. Синтезируется линейное корректирующее устрой­ство также методом линейной теории.

4. Вычерчивается логарифмическая фазовая частот­ная характеристика полученной скорректированной ли­нейной части системы.

В дополнение ко всем этим операциям, выполняемым по линейной теории, добавляется еще один пункт, учи­тывающий нелинейность F(x) в нормированном виде.

5. Для данной нелинейности с использованием норми­рованного коэффициента q0(a) строится «запретная» зона, соответствующая желаемому показателю колебательности М. Внутрь этой зоны не должна заходить фазовая частотная характеристика скорректированной линейной части системы. Та кривая М = const, которой касается полученная фазовая характеристика, определяет значение показателя колебательности данной скорректированной системы. Если необходимо его уменьшить, тонужнонесколько изменить параметры полученного выше линейного корректирующего устройства, следя за тем, чтобы не допускать существенного искажения желаемых свойств логарифмической амплитудной частотной характеристики приведенной линейной части, положенных первоначально в основу расчета.

Этот пятый пункт процедуры синтеза в совокупности с предыдущими обеспечивает нужные качества процессов в замкнутой нелинейной системе в целом. Следовательно, прежде чем приступать к синтезу линейного корректирующего устройства в нелинейной системе, необходимо научиться строить запретную зону по показателю колебательности при заданной нелинейности. Такое построение может производиться методом гармонической линеаризации, поскольку речь идет о колебательных переходных процессах.

Рассмотрим методику этого построения. Ограничиваясь рассмотрением однозначных нелинейностей (7.1) с ограниченными значениями коэффициента гармонической линеаризации (7.2) и используя его нормирование (7.3), получим следующее выражение для передаточной функции разомкнутой цепи гармонически линеаризованной системы:

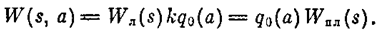
Передаточная функция замкнутой системы приметвид

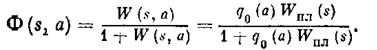
Выделим вещественные и мнимые части после заме­ны s = jw, обозначив их следующим образом:

Тогда для показателя колебательности М = ½Ф(jw, a)½ имеем выражение

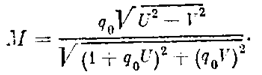
Отсюда после преобразования получаем уравнение линии равных значений М на комплексной плоскости (U, V) в виде

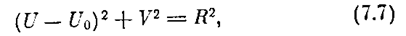
где

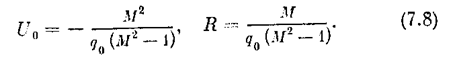
При определенном значении q0 линии М = const по­лучают вид окружностей. Но согласно (7.2) и (7.3) ве­личина q0 может принимать любое значение в интервале

0 £ q0(a) £ q0 m или q0 н £ q0(a) £ q0 m (7.9)

где числа q0 н и q0 m получают свои определенные значе­ния для каждой конкретной нелинейности. В соответствии с этим, согласно (7.8), координата центра окружно­сти U0 и радиус R будут тоже меняться в определенных

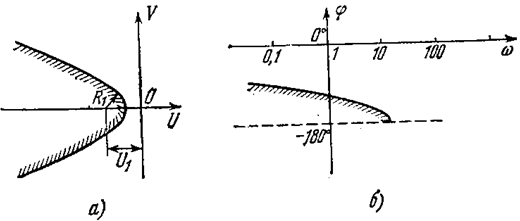
Рис. 7.2.

для каждой нелинейности пределах. Следовательно, каж­дая линия М = const будет определяться как огибающая непрерывного множества постепенно меняющихся окружностей. При этом в случае первого неравенства (7.9) линия М=const будет незамкнутой (рис. 7.2, а), так как в начальной точке q0 = 0 из (7.8) имеем U0 =¥, R = ¥. Показанные на рис. 7.2, а величины R1 и U1, согласно (7.8), определяются выражениями

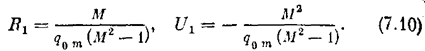
В случае второго неравенства (7.9) линия M = const бу­дет замкнутой (рис. 7.3, а), причем

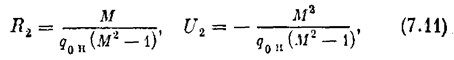
а значения R1 и U1 прежние.

Рис. 7.3.

Поскольку синтез линейного корректирующего уст­ройства проводится по логарифмическим частотным ха­рактеристикам, то изображенные на рис. 7.2, а и рис. 7.3, а

Рис.7.4.

линии М = const (запретные зоны) должны быть перенесены в систему координат ло­гарифмических характе­ристик. Это показано соот­ветственно на рис. 7.2, б и рис. 7.3, б.

Взяв разные постоян­ные значения М(М1, М2, М3 ,…), получим серию кривых М = const (рис. 7.4).

Логарифмические частотные характеристики скорректиро­ванной по изложенной выше процедуре системы должны быть такими» чтобы фазовая характеристика линейной

Рис. 7.5.

Рис. 7.6.

части j(w) не заходила внутрь запретной зоны,определяемой допустимым значением показателя колебательности М (рис. 7.5).

Если расчет корректирующего устройства ведется по амплитудно-фазовым частотным характеристикам, то поле координат (U, V) получается серия кривых M = const (рис. 7.6, а), причем амплитудно-фазовая частотная характеристика приведенной линейной частискорректированной системы не должна заходить внутрьзапретной зоны, определяемой здесь допустимым значением показателя колебательности М (рис. 7.6, б).

Пример. Пусть имеется два варианта (рис. 7.7, а и б) нелинейности F(x) в системе, изображенной нарис. 7.1. Передаточные функции линейных звеньев (рис. 7.1) заданы в виде

Следовательно,

Заданы Т1= 0,01, Т2 = 0,04, а величину kл можноизменять.

Рис. 7.7.

Крутизна наклона линейных отрезков нелинейной характеристики определяется коэффициентами k3 и k4.

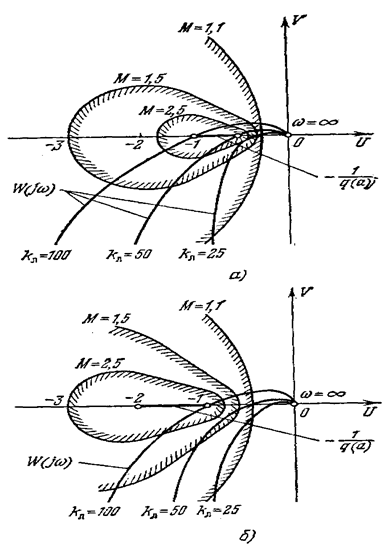
Рис. 7.8.

причем в первом случае (рис. 7.7, a) k3 = 1, k4 = 2,а во втором случае (рис. 7.7, б) k3 = 1, k4 = 0,5. Здесь нелинейность представлена уже в нормированном виде, поскольку k3 = 1. Поэтому тут q0(a) = q(а). Очевидно, что коэффициент q (a) меняется в пределах между k3 и k4 т. е. в первом и втором случаях соответственно име­ем 1 £ q0(а) £ 2; 0,5 £ q0(a) £ 1. Линия М = const будет иметь вид, представленный на рис. 7.3, где, согласно

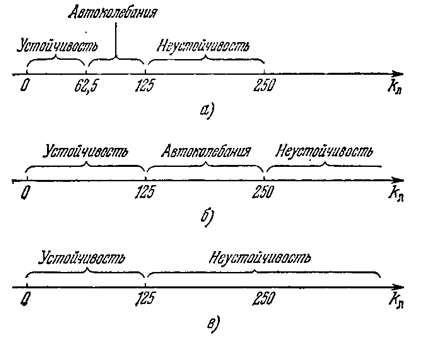
Рис. 7.9.

(7.10) и (7.11), для первого случая (рис. 7.7, а)

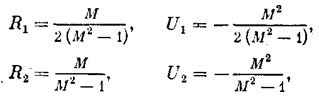
а для второго (рис. 7.7, б)

Придавая М разные значения, получаем кривые, по­казанные на рис. 7.8, а и б соответственно для первого и второго случаев. Там же нанесены амплитудно-фазовые характеристики линейной части для трех разных значений k л. Из этих графиков видно, что по сравнению с чисто линейной системой в первом случае (рис. 7.8, а) за счет нелинейности запретная зона выпучивается впра­во а во втором (рис. 7.8. б) - влево. Следовательно, в первом случае за счет нелинейности повышается коле­бательность системы, а во втором - нет. Интересно так­же отметить то, что автоколебания в нелинейной систе­ме определяются (см. лекцию 17) условием

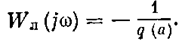
Правая часть этого равенства изображается графиче­ски отрезками вещественной оси соответственно для пер­вого и второго случаев:

-1 £ U £ -0,5,

-2 £U £ -1. Линейная же система устойчива, если кривая W (jw) пересекает вещественную ось правее точки -1. Следова­тельно, во втором случае область устойчивости нелиней­ной системы сохраняется, как в линейной системе, а ав­токолебания возникают уже за ее пределами. В первом же случае область устойчивости системы за счет нели­нейности сужается, и автоколебания возникают там, где линейная система была бы устойчива.

На рис. 7.9 это показано графически: а) для первого случая, б) для второго случая, в) для чисто линейной системы.

 

ЛЕКЦИЯ 30, 31 Нелинейные корректирующие устройства.

План.

1. Система с нелинейной обратной связью.

2. Система с сигналом нелинейной коррекции.

3. Система с ограничением линейности обратной связи.

 

Специального вида нелинейности можно вводить в линейную систему в качестве корректирующих устройств; в результате этого в скорректированном виде линейная система становится нелинейной. Коррекцию с помощью нелинейных устройств производят также и в нелинейных системах. Нелинейная коррекция обладает более широкими возможностями, чем линейная, так как она, во-первых, дает большее разнообразие форм частотных ха­рактеристик и, во-вторых, она позволяет менять форму частотных характеристик в зависимости от величины амплитуды сигнала. Последнее свойство нелинейной коррекции является принципиально новым качеством по сравнению с линейной коррекцией. Оно придает системе как бы свойство самонастройки по величинеошибкивозникающей в системе в процессе управления.

Задачи нелинейной коррекции могут заключаться, какобычно, в достижении желаемых свойств процессов управления, причем должна предусматриваться возможность изменения этих свойств с изменением величина отклонения. Таким образом, открывается возможности преодолевать известное из линейной теории [23] противоречие между требованиями точности и требованиями устойчивости системы, а также значительно усиливать регулирующее воздействие при больших отклонениях и т. п.

Кроме того, если в заданной нелинейной системе имеются вредные для процесса нелинейности (люфт, гистерезис, зона нечувствительности), то путем введений

Рис. 7.10.

специальной нелинейной коррекция можно в известной мере ослабить вредное влияние имеющихся в системе неизбежных нелинейностей.

В качестве первых примеров рассмотрим введение нелинейного корректирующего устройства в линейную систему.

1. Проанализируем систему с нелинейной обратной связью, сигнал которой уменьшается с возрастанием ошибки. Схема такой системы показана на рис. 7.10. Напряжение, пропорциональное модулю ошибки, подается на вход умножителя и затем вычитаетсяиз выходного напряжения тахогенератора, находящегося в цепи линейной обратной связи. Сигнал обратной связи уменьшается, когда ошибка возрастает, что приводит к убыстрению отработки больших отклонений и уменьшению скорости отработки в конце процесса. Динамика системы описывается уравнениями

Уравнение системы в переходном процессе без внеш­него воздействия (q1 = 0) имеет вид

где kос = k2 k3 k5, k’ос = k1 kв kос, k = k1 k2 k4. Гармониче­ская линеаризация входящей сюда нелинейности F(x) = ½ х ½р х для переходного процесса, согласно (6.48), дает

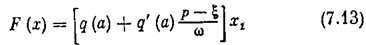
где по формулам (4.11) с учетом (6.47) для данной не­линейности имеем

 

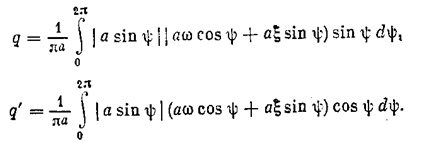
После интегрирования получаем

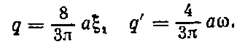
Тогда характеристическое уравнение системы (7.12) примет вид

Подстановка l = x + jw дает два уравнения

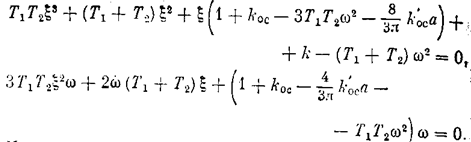
Из второго уравнения

а из первого —-

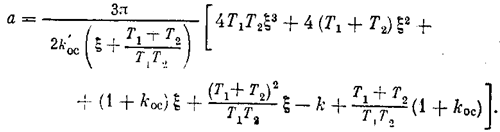
На основании этих двух формул можно построить диаграммы качества нелинейных переходных процессов (см. лекцию 27) по любому параметру, например по парамет­ру k. Можно также при всех заданных параметрах опре­делить зависимости x(а) и w(а) и произвести оценки качества переходных процессов.

2. Рассмотрим более совершенную систему, схема ко­торой изображена на рис. 7.11. Система отличается от прежней тем, что сигнал нелинейной коррекции uоспроходит через контакты реле. В результате при u5 < 0 (т. е. в четных четвертях колебаний) сигнал нелинейной коррекции не подается на вход усилителя. Это — сущест­венное улучшение в сравнении с предыдущей системой, так как там уменьшение демпфирования давалось во всех четвертях колебаний, в то время как в четных чет­вертях это уменьшение пользы не приносят. Здесь оно исключается за счет отключения коррекции при u5 < 0.

Pис.7.11.

В результате вместо уравнения (7.12) теперь полу­чим

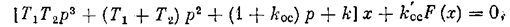
где

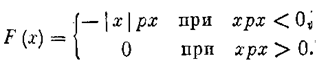
Коэффициенты гармонической линеаризации изменят­ся при этом следующим образом:

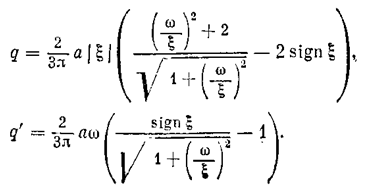
Подставив это в общую формулу (7.13), получим

Характеристическое уравнение гармонически линеаризо­ванной системы примет вид

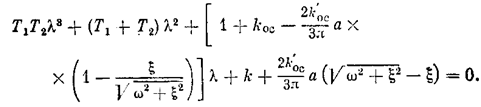
После подстановки l = x+jw отсюда получаются два уравнения. Каждое из них дает возможность выразить величину а в явном виде:

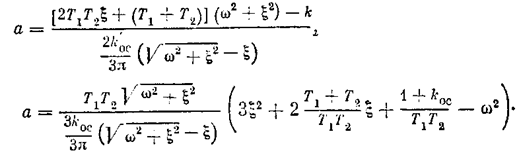
Графическим решением этой системы двух уравнений можно найти значения а и w для каждого заданного значения x. В результате получаются зависимости w(a) и x(а), характеризующие качество переходных процессов при заданных параметрах системы. Если же менять k или другой параметр системы, то можно построить и диаграммы качества нелинейных переходных процес­сов в этой системе по любому параметру.

3. Система с ограничением линейности обратной свя­зи схематически показана на рис. 7.12. Уравнения ее заданы в виде

где F(wд) - нелинейность, изображенная на рис.7.12.Применение такой нелинейной обратной связи позволяет уменьшить величину ошибки в динамике при большой скорости отработки (улучшает качество переходного процесса сохраняя возможность обеспечения необходимого значения kос при малых скоростях, исходя из требования

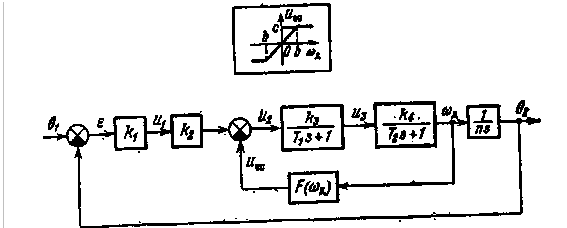
Рис. 7.12.

статической точности. Гармоническая линеаризация для переходного процесса здесь, согласно лекции 27, дает

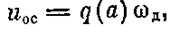
причем

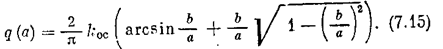
Характеристическое уравнение системы:

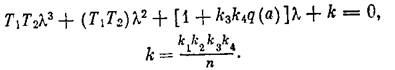
Из двух уравнений, получаемых после подстановки l = x +jw, находим

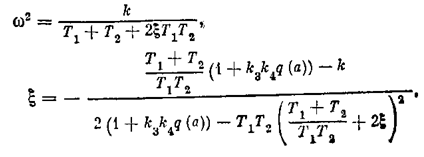
Построим зависимости x(а) при разных значение параметра x, входящего в выражение для q (a) (7.15) и определяющего зону линейности характеристикиобратной связи (рис, 7.12). Эти зависимости x(а) показаны

Рис.7.13.

на рис. 7.13. По величине x(а) можно составить оценку длительности переходного процесса и выбрать наилучшее значение b.

4. Приведем, наконец пример введения нелинейной коррекции в нелинейную ав­томатическую систему. Схема системы представлена на рис. 7.14. Система имеет релейное управление. В качестве корректирующего уст­ройства введена нелинейная обратная связь по скорости с параболической характеристикой

uос = kос х ²sign x, x = pb.

После гармонической линеаризации имеем

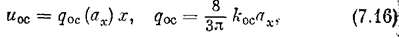
где а х — амплитуда колебаний скорости х = рb. Релейная характеристика

в результате гармонической линеаризации принимает вид

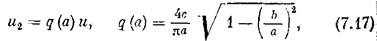
где а - амплитуда колебаний переменной u. Передаточ­ные функции линейных звеньев системы указаны на схеме рис. 7.14.

Характеристическое уравнение гармонически линеа­ризованной системы получает вид

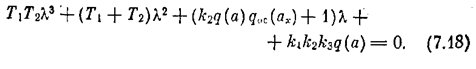
Выразим амплитуду а х, через а. Согласно схеме рис. 7.14 получаем

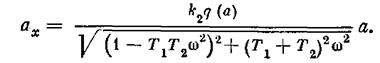
Тогда по формуле (7.16) получаем

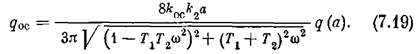
Исследуем устойчивость данной системы с нелиней­ной обратной связью и сравним со случаем, когда, в той же

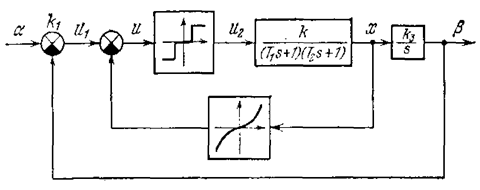
Рис. 7.14.

релейной системе обратная связь линейна, т. е. когда величина qос заменяется просто коэффициентом kос. Гра­ницу устойчивости будем искать как границу области существования автоколебаний согласно указанию в кон­це лекции 22.

Подставив в характеристическое уравнение (7.18) l = jw получим

Эти два уравнения с подстановкой (7.19) определяют частоту w и амплитуду а автоколебаний. Выполнение равенств (7.20) соответствует прохождению кривой Ми­хайлова (при данном значении а) через начало координат (кривая 1 на рис. 7.15). Для устойчивости системы (отсутствие автоколебаний) нужно, однако, чтобы уравнения (7.20) не удовлетворялись и кривая Михайлова охватывала бы начало координат (кривая 2 на рис. 7.15), т.е. чтобы при Х= 0 выполнялось условие Y0(a) > 0при любом значении а. Удобнее пользоваться выражением

Поскольку параметр w > 0, то данное условие устойчивости

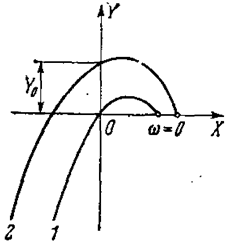
Рис. 7.15.

можно записать в виде

Из условия Х = 0, согласно (7.20) выразим параметр w через величину а: '

и подставим его в выражение для Y(a), используя одновременно и подстановку (7.19). В результате получим условие устойчивости (7.21) в виде

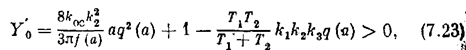
где

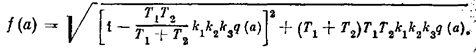
В случае, если в данной релейнойсистеме обратная связь линейна, т. е. qос = kос, получим согласно (7.20) более простое выражение условия устойчивости:

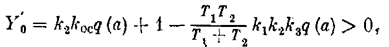
или

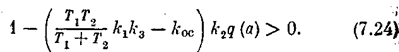
Отсюда видно, что если

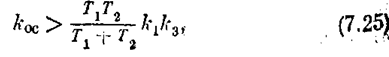
то система устойчива при любых значениях коэффициен­та усиления k2 и сигнала с реле. При

Рис.7.16.

условие (7.24) будет удовлетворено при всех значениях а в том случае, если оно удовлетворяется при наибольшем значении q. График q(а), согласно (7.17), имеет вид, изображенный на рис. 7.16, а условие устойчивости релейной системы с ли­нейной обратной связью (7.24) принимает вид

В соответствии с этим на рис. 7.17 изображена область устойчивости на плоскости k2 kос а случаелинейной обратной связи.

Рис. 7.17.

Аналогично на основании выражения (7.23) запишем условие устойчивости релейной системы с нелинейной обратной связью:

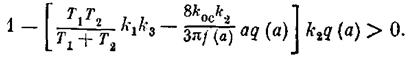
Здесь также надо потребовать удовлетворения этого условия при наибольшем значении q(a). Условие устойчивости примет вид

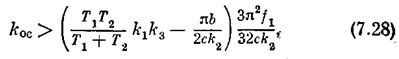
где

Поскольку в первом грубом приближении величинаf1пропорциональна величине сk2, то характер очертания границы устойчивости сохранится. Если при этом множитель за скобкой в выражении (7.28) можно сделать меньшим единицы, то за счет нелинейности обратной связи можно расширить область устойчивости, как показано на рис. 7.17,

 

ЛЕКЦИЯ 32,33 Псевдолинейная коррекция.

План.

1. Псевдолинейные корректирующие устройства.

2. Коррекция апериодического звена.

3. Коррекция инерционности дифференцирующего контура.

4. Нелинейный фильтр с фазовым опережением.

Псевдолинейными корректирующими устройствами называются такие нелинейные корректирующие устройства, у которых эквивалентные передаточные функции (а значит, и коэффициенты гармонической линеаризации), в отличие от рассмотренных в предыдущей лекции, зависят только от частоты и не зависят от амплитуды. Однако эта зависимость от частоты—нелинейная в том смысле, что характер ее отличается от частотной зависимости линейных передаточных функций и может быть произвольным, т. е. отсутствует жесткая связь меж­ду амплитудными и фазовыми характеристиками, которая имеется у линейных звеньев. Это важное достоинство псевдолинейных устройств позволяет корректировать фазовые соотношения независимо от амплитудных и наоборот, что невозможно сделать линейными средствами.

Результат гармонической линеаризации при исследовании устойчивости для псевдолинейного устройства F(x) имеет вид

а при исследовании колебательных переходных процессов

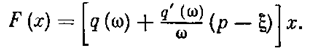
Эти выражения можно представить в другой форме:

где для исследования устойчивости имеем

а для колебательных переходных процессов

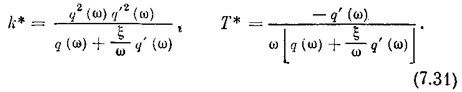
Такие псевдолинейные корректирующие устройства тоже обладают большими дополнительными возможностями улучшения качества процессов управления по сравнению с линейными устройствами.

Приведем несколько примеров.

1. Коррекция апериодического звена. Ставится задача существенного уменьшения инерцион­ности, т. е. отставания выходного сигнала по

y = arctg Тw апериодического звена

(Tp+1) у = k х, (7.32)

В одной из возможных схем такой коррекции (рис. 7.18, а) при помощи ключа отсекаются хвостовые части выходного сигнала, причем последний приобрета­ет форму, показанную штриховкой на рис. 7.18, б. Тогда выражения (4.11) для коэффициентов гармонической ли­неаризации примут вид

где y = arctg Тw. Видно, что q и q' будут зависеть лишь от частоты w, но не от амплитуды, что характерно для псевдолинейных корректирующих устройств. Применяя другую форму гармонической линеаризации (7.29), получим для скорректированного апериодического звена вместо (7.32) уравнение

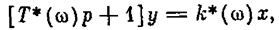
в котором новые эквивалентные постоянная времени Т* и коэффициент усиления k * определяются формулами

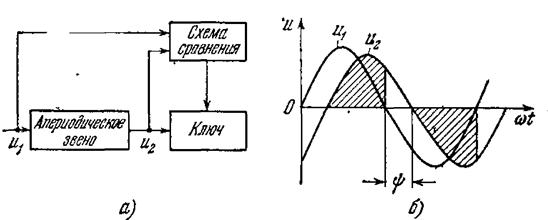
Рис. 7.18.

(7.30) или (7.31) через найденные уже q(w) и q’(w). На рис. 7.19 приведены графики их зависимости от час­тоты. Видно существенное снижение инерционности (например,

Pис.7.19.

при wТ = 2 получается примерно Т* = 0,5Т), но при этом примерно во столько же раз снижается и усиление k*.

Лучший эффект получается при введении дополни­тельного упреждения g (рис. 7.20) при ключевом вырезании части выходного сигнала.При этом получается

Графики для Т * и k* в зависимости от w приоб­ретают вид, показанный на рис. 7.21. Таким способом

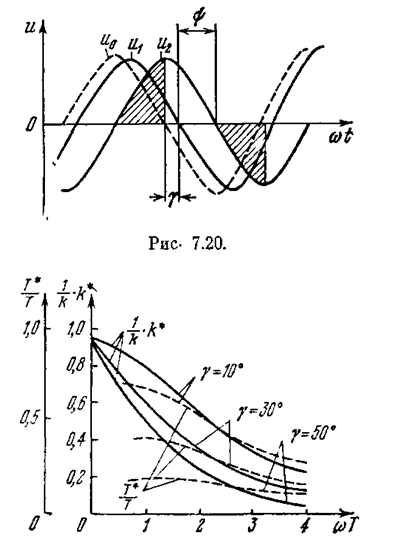
Рис.7.21.

можно уменьшать фазовое запаздывание в тех звеньях системы, которые обладают большой постоянной времени, плохо влияющей накачество процесса управления.

2. Коррекция инерционности дифференцирующего контура. Задана схема системы с дифференцирующим контуром F(u) (рис. 7.22), нелинейность которого состоит в коррекции его инерционности.

 

Рис. 7.22.

Рис. 7.23.

как показано на рис. 7.23. Выходной сигнал, обозначен­ный штриховкой, в хвостовой своей части изменяет знак на противоположный.Тогда вместо линейного диффе­ренцирующего звена

(Tp+1) у = Трu

получаем нелинейное (псевдолинейное) с эквивалентным уравнением

где

g — заданное опережение, y = arctg Tw. Величина q'

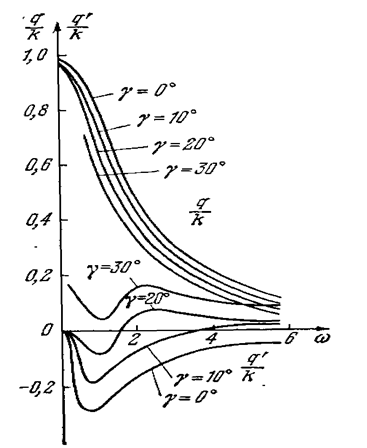
Рис. 7.24

может быть сделана положительной. Зависимость коэф­фициентов гармонической линеаризации q и q' от частоты колебаний w показана на рис. 7.24 при различных заданных опережениях g.

Уравнение для ошибки системы (см. рис. 7.22) получает вид

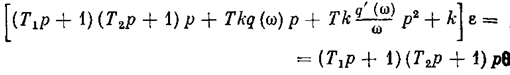
где k = k1 k2 k3 k4 k5. Характеристическое уравнение системы

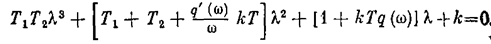
Частота определяется формулой (после подстановки l = jw:

Граница устойчивости Dn-1 = 0 описывается выражением

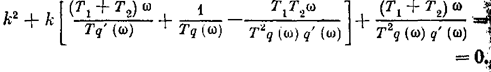
Исследование показывает, что область устойчивости системы за счет такой коррекции значительно увеличивается

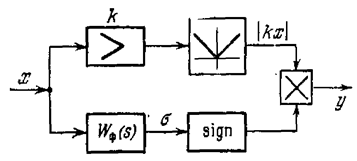
Рис. 7.25.

т. е. можно существенно повысить общий коэффициент усиления k, не вызывая неустойчивости системы.

3. Нелинейныйфильтр с фазовым опере­жением. Схема, показанная на рис. 7.25, позволят получить фазовое опережение без изменения амплитуды. Она аналогична звену переменной структуры, но вместо сложения сигналов введено умножение модуля ½k x ½ на sign s,

Рис. 7.26.

где s—выход линейного фильтра Wф(s), создающего опережение. На рис. 7.26 приведены нелинейные характеристики этой схемы при разных значениях опережения a, получаемых выбором параметров схемы.Так, при 0 < a < p/2 имеем

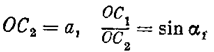
а при p/2 < a < p

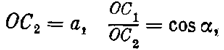
где а - амплитуда входных колебаний, причем при a = p / 2 точки С1 и С2 сливаются. Если линейная часть фильтра имеет вид

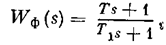
то опережение

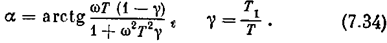
Для коэффициентов гармонической линеаризации имеем формулы

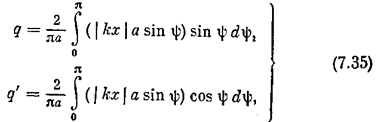
причем интегралы разбиваются на два с пределами соот­ветственно (0, a) и (a,p). В результате получаем

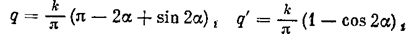
где a = f(w) выражается формулой (7.34).Как видим, данная нелинейная схема относится к классу псевдоли­нейных. Получаемое фазовое опережение

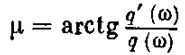
показано на рис. 7.27 при разных значениях g в зави­симости от частоты w, отложенной по логарифмической шкале.При этом амплитудное искажение Q (w) опреде­ляемое величиной

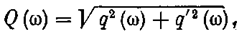
оказывается незначительным (менее 4 дБ), что вполне приемлемо для решения поставленной задачи.

Рис. 7.27.

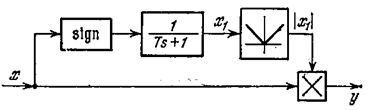
Рис. 7.28.

4.Нелинейный фильтр с амплитудным ослаблением. Схема, изображенная на рис. 7.28, позволяет получить ослабление амплитуды с ростом частоты без изменения фазы. Выходной сигнал у = ½ х 1½ х связан с х соотношением

(Тр+1) х 1 = sign х.

Формы колебаний входящих сюдапеременных при х = a sin wt показанына рис.7.29, причем

где

Используя формулыгармонической линеаризации (7.35), нужно заменить этих формулах k x на х 1 и

Рис.7.29.

Рис. 7.30.

разбить каждый интеграл на два: (0, a) и (a, p) где a - точка перемены знака х 1 (см. рис. 7.29). определяе­мая выражением

Результат интегрирования

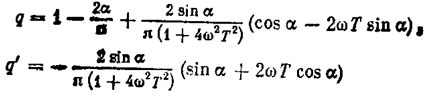
(снова отмечаем зависимость q и q' только от частоты, но не от амплитуды). На рис.7.30 показана амплитудная характеристика

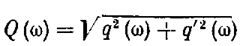
такого псевдолинейного фильтра. Из характеристики вид­но эффективное подавление амплитуды колебаний. Лег­ко проверить, что фазовое искажение при этом незначи­тельно.

 

ЛЕКЦИЯ 34 Системы с переменной структурой.

План.

1. Описание системы.

2. Условия возникновения скользящего режима.

3. Пример.

 

Некоторые простейшие вопросы, связанные с системами с переменной структурой уже затрагивались нами ранее в лекции 8. Вообще говоря, в таких системах возможны различные виды процессов. Но, как отмечалось в лекции 8, особый интерес представляет такое формирование управляющего устройства в системе с переменной структурой, которое реализует скользящий процесс. Преимущество последнего состоит, в частности, в том, что его форма не зависит от параметров основной части системы и может протекать с желательными для конструктора свойствами. Поэтому дальше будет излагаться только задача построения систем переменной структуры с организацией скользящего, режима.

Схема системы представлена на рис. 7.31. Пусть динамика основной части системы (управляемый объект с исполнительным устройством) при отсутствии внешнего воздействия описывается уравнением

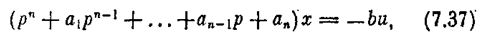
где х — отклонение регулируемой величины, u — управляющий сигнал на исполнительное устройство. Обозна­чим

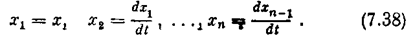
Тогда уравнение (7.31) можно представить в виде системы

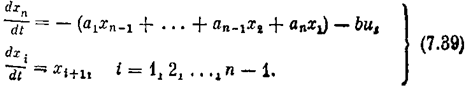
Функцию управления с переключением структуры, формируемую в логическом управляющем устройств выберем в виде

где

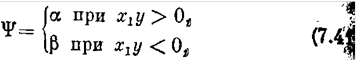
причем a, b — постоянные коэффициенты (a > b), а переменная у

Рис. 7.31.

складывается из отклонения х 1и n-1производных:

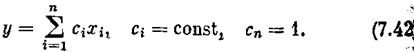
В этом случае говорят, что имеется полная информация о состоянии системы. На практике же иметь точные значения всех производных невозможно.

Сначала рассмотрим идеализированную систему в конце лекции будет сказано о реальном случае систем с неточной и неполной информацией). Переключение структуры будет происходить, согласно (7.41) и (7.42), при

В n -мерном пространстве это будет гиперплоскость. Напомним, что на фазовой плоскости (лекция 8) мы имели пря­мую линию переключения (2.26), а в трехмерном прост­ранстве это была бы обычная плоскость (для системы третьего порядка, когда п = 3).

Условие возникновения скользящего процесса состоит в том, чтобы фазовые траектории встречались на гиперплоскости переключения, подходя к ней с обеих сторон, дли же принадлежали бы этой гиперплоскости. (В систе­ме второго порядка они встречались на линии переклю­чения (рис. 2.18).) Следовательно, требуется, чтобы, с одной стороны, гиперплоскости переключения (7.43), где у > 0, производная d y /dt была неположительной, а с другой стороны, гиперплоскости, где у < 0, производная d у /dt была неотрицательной. Это условие возникновения скользящего процесса можно записать в виде

где ± 0 обозначает пределы стремления у к нулю со стороны соответственно положительных и отрицатель­ных значений у.

Определим вид дифференциального уравнения, кото­рым описывается скользящий процесс. Согласно (7.43), (7.42) и (7.38) получим для скользящего процесса сис­тему уравнений