Аппроксимация дифференциального оператора 
, сетка, разные шаблоны и погрешность аппроксимации.
Рассмотрим дифф. оператор 
на примере одномерной нестационарной задачи теплопроводности.
, 
, 
.
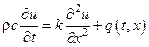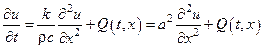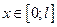Произведём обезразмеривание задачи:
, 
, 
.
, 
, 
.
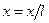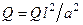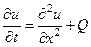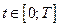Добавим Г.У.:
Вводим прямоугольную сетку: 
Вводим сеточные функции 
, 
.
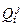Можно использовать два вида 4-х точечного шаблона. Запишем в виде суммы:
, 
, 
, 
.
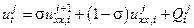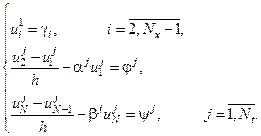
При 
мы получаем явную разностную схему. При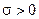 
– неявная, причём при 
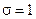– чисто неявная, а при 
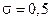– неявная симметричная или Кранка–Николсона.
Доказано, что для схем при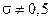 
порядок аппроксимации составляет 
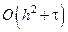, а для симметричной схемы при – 
.
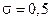Порядок же аппроксимации краевых условий уравнениями имеет первый порядок относительно h.
Явные схемы имеют несомненное преимущество перед неявными в простоте организации вычислений. Однако большинство явных схем являются условно устойчивыми и это снижает их эффективность. Условная устойчивость означает, что не для всех соотношений шагов по времени и координате решение будет сходиться к истинному результату. Ограниченность решения при 
есть основной практический критерий устойчивости разностной схемы!
Если же возникающие в процессе расчетов вычислительные погрешности имеют тенденцию убывать (по крайней мере, не возрастают), то разностная схема называется устойчивой. Т.е. малому изменению входных данных соответствует малое изменение решения.
Отличительной особенностью явных схем является то, что при их использовании должно соблюдаться некоторое условие, обеспечивающее сходимость и устойчивость метода, в противном случае будут накапливаться ошибки в ходе вычислений. Для каждого вида уравнений проводится анализ устойчивости и определяется критерий сходимости (если это возможно сделать).
В общем случае разностное решение или его устойчивость может зависеть от правой части, граничных условий и начальных условий. Поэтому различают три вида устойчивости: по правой части, граничным условиям и начальному условию.
Для нашего дифф. оператора исходя из теоремы об устойчивости Неймана условие устойчивости для схем при 
имеет вид: 
.
Многомерные задачи. Обычная РС, шаблон типа крест.
Численные исследования нестационарных задач в дух и трехмерных пространствах значительно сложнее задач в одномерной постановке. При этом не вызывает затруднений в построении самого разностного аналога краевых задач. Однако число неизвестных в разностных схемах в многомерных случаях значительно возрастает.
Пусть задана краевая задача на прямоугольнике.
, 
, 
, .
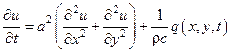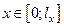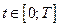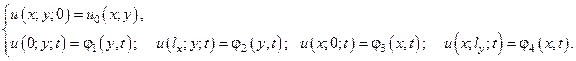
Вводим сетку: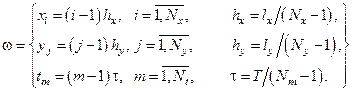 
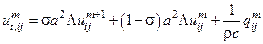, где
,
.
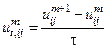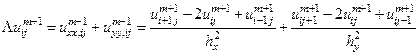+ граничные условия и начальное условие
Скорость сходимости аппроксимации основного уравнения для симметричной неявной схемы 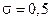составит: 
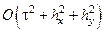. В противном случае: 
.
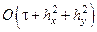Как и в одномерном случае при явная и неявная схемы имеют условие устойчивости вида: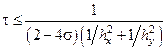 
.
Явная – объем вычислений пропорционален числу узлов разностной схемы, неявная – безусловно устойчива. Разностные схемы, сочетающие эти положительные свойства, называются экономичными.
Наибольшее распространение получили разностные схемы, основанные на методе дробных шагов по временной переменной. Экономичность решения задач с помощью разностных схем, основанных на методе дробных шагов, достигается сведением многомерной задачи к решению последовательности одномерных, для решения которых может быть использован эффективный метод прогонки.
Запишем полуцелый шаблон по «продольно-поперечной» схеме (метод переменных направлений):
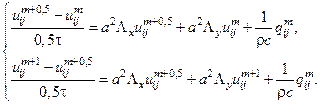
Из первого уравнения определяются промежуточные значения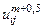 
на половинном шаге. Это уравнение неявно по координате 
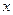и явно по координате 
. При любом фиксированном 
первое ур. можно решить прогонкой по 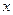. Второе уравнение схемы неявна по и явна по 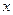. Тоже решается прогонкой, только по .
Для получения Г.У. при решение задачи относительно нужно знать решение на границе на получелом слое. Если из второго уравнения схемы вычесть первое:
.
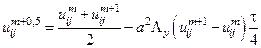Записав это соотношение в первой и последней точке и получим новые Г.У. для решения задачи на слое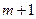 
.
После некоторых преобразований из вышеуказанных схем можно получить следующую схему:
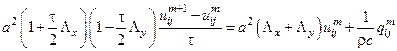или
.
Разностная схема с оператором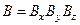 
, где каждый из операторов-множителей является одномерным и допускает обращение методом прогонки, называется схемой с факторизованным оператором.
Рассмотренная схема используется для нестационарных систем, однако, в ряде случаев, её можно применять для решения стационарных задач, решение которых можно рассматривать как установившееся решение соответствующей нестационарной задачи при 
. Сам процесс установления роли не играет, а время в разностной схеме играет роль параметра. Расчёт схемы идёт до выполнения условия: 
.