Классификация конечных элементов
- по форме и размерности: одномерные, двух мерные – треугольный, прямоугольный – трёхмерные – тетраэдр и пр.
- по характеру аппроксимации неизвестных в элементе: по степени аппроксимационного полинома – линейный, квадратичный, кубический и т.д.;
- по способу задания узловых неизвестных: элементы с лагранжевой аппроксимацией – в качестве узловых неизвестных выбираются значение искомой функции; элементы с эрмитовой аппроксимацией – в качестве узловых неизвестных выбираются значения искомой функции и её первых производных по координате;
- по аппроксимации перемещений и геометрии: изопараметрические – геометрия элемента описывается полиномом той же степени, что и неизвестные в элементе; субпараметрические – степень полинома аппроксимации неизвестных ниже степени полинома, описывающего геометрию; суперпараметрический – наоборот.
- совместные – значения функции, выбранной в качестве узловых неизвестных, непрерывным образом изменяются вдоль общих границ соседних КЭ (на границах нет разрыва полей неизвестных функций, однако разрыв производных может наблюдаться) и, очевидно, несовместные КЭ.
Под аппроксимацией заданной функции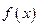 
понимается выбор функции 
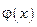из некоторого определенного класса (например, среди алгебраических многочленов заданной степени), в том или ином смысле близкой к 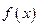и дающей её приближенное представление.
Интерполяция – частный случай аппроксимации, когда приближение происходит на отрезке между узлами некоторой сетки, а в узлах сетки значения интерполяции совпадает с известным значением функции.
Симплекс-элемент. Основные матричные соотношения.
Нарисовать элемент. Строим сетку и на ней задаём неизвестные и пр.
.
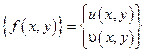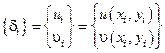– перемещение узловой i -ой точки,
.
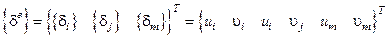Здесь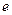 
– номер элемента внутри сетки.
, 
, 
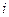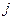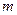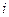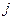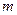– локальная индексация узлов (сами же значения , и отвечают за глобальные номера узлов).
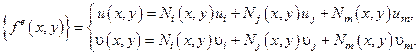
Выбираем функции форм в виде линейного полинома: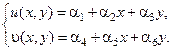 
Зная, что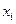 
и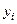 
мы должны получить 
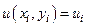и, очевидно, 
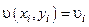и так для всех узлов элемента, то можно составить две СЛАУ и получить (методом Крамера, например) параметры альфа – вывести самим дома! В результате мы получим
,
.
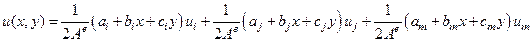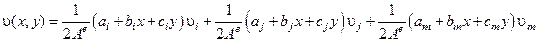где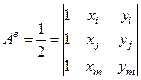 
– площадь КЭ (площадь треугольника).
Здесь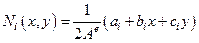 
– функция формы КЭ,
где
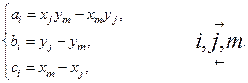
Ф.ф. обладает свойством: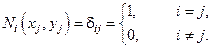 
(нарисовать) И ещё свойством ортогональности.
Нумерация узлов против часовой стрелки (или наоборот, но для всех элементов одинаковая) – площадь элемента будет положительна.
Итак,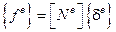 
– перемещение в элементе через узловые перемещения.
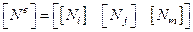, где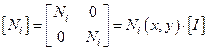 
и т.д.
.
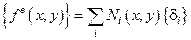Из геометрических соотношений имеем
.
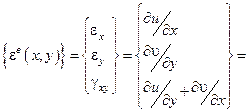
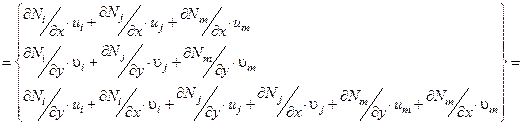
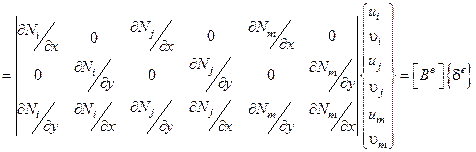Или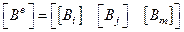 
– матрица градиентов, где 
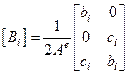– матрица градиентов, состоит из констант, поэтому в симплекс-элементе 
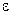не зависят от координат и одинаковы во всех точках элемента.
Из закона Гука (физ. соотн. при ПДС)
.
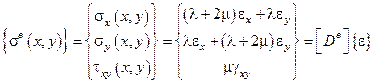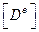– матрица упругих констант, связывает напряжения и деформации.
– ПДС.
Для ПНС имеем 
, где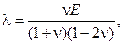 
.
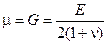Тогда
.
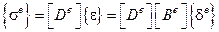Из принципа возм. перемещений:
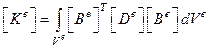– справедлива для любого КЭ. Для сипмлекс-элемента имеет размер 
.
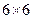В случае плоской задачи ТУ для симплекс-элемента имеем:
,
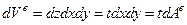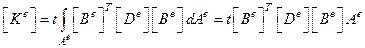т.к.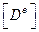 
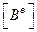– константы.
Вычислим вектора узловых сил для симплекс-элемента. Всего 5 видов сил: объёмные, поверхностные, сосредоточенные, структурных изменений (свободные температурные деформации) и силы от остаточных напряжений.
Объёмные силы.
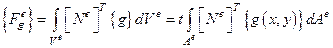– столбец объемных узловых сил.
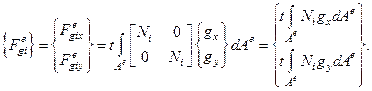
Пусть внешние силы постоянны в пределах одного конечного элемента.
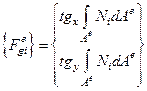. (доказать самостоятельно, что 
)
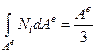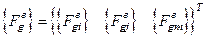, где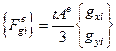 
.
Поверхностные силы: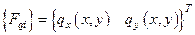 
.
.
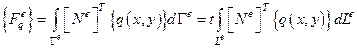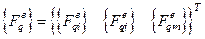, где в случае попадания на границу только узлов 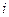и 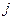будет выполняться 
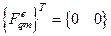, для остальных векторов при постоянной нагрузке
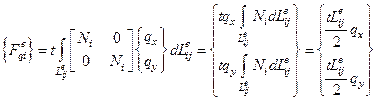
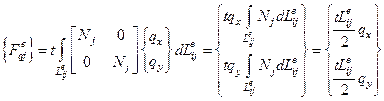
(доказать самостоятельно, что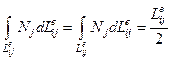 
).
Сосредоточенные силы: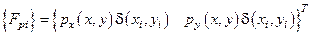 
, где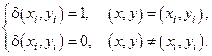 
Нарисовать пример для точки 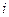(помним, что 
):
.
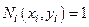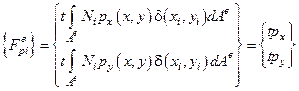Усилия от свободных деформаций.
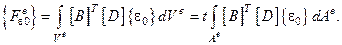
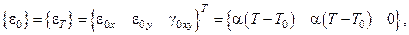
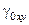– сдвиговые деформации, не зависят от 
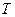. Пусть в каждом элементе температура постоянна, тогда
.
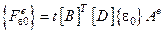Самостоятельно вывести формулу для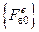 
в случае ПНС и ПДС!
Усилия от остаточных напряжений: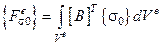 
, где
.
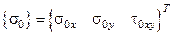