Осесимметричный конечный элемент.
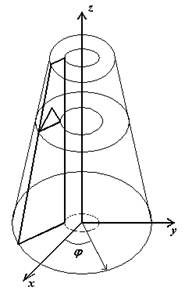
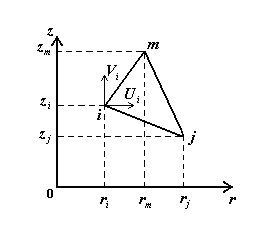
Вводим вектор неизвестных в элементе:
.
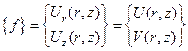Вектор узловых неизвестных:
, 
.
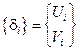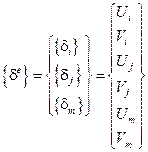Аппроксимацию неизвестных внутри элемента, как и для симплекс-элемента, выбираем в линейном виде.
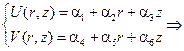
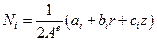, где 
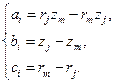
Матрица функций формы будет аналогична симплекс-элементу:
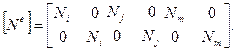
Исходя из геометрических соотношений для осесимеетричной задачи ТУ, имеем
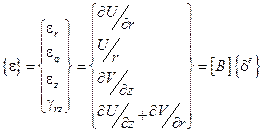, где матрица градиентов есть блочная матрица
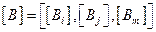, где каждый блок в свою очередь имеет вид
.
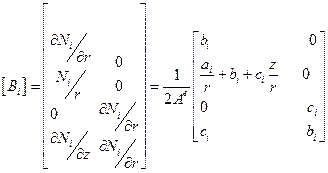Запишем физические соотношения, то есть закон Гука для осесимметричной задачи
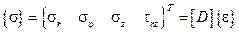, где матрица упругих констант имеет вид
.
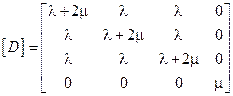Из принципа возможных перемещений, как обычно, получаем
.
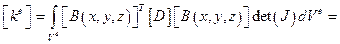
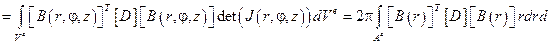Здесь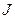 
– якобиан, матрица перехода из декартовой системы в цилиндрическую. Переход из декартовой системы в цилиндрическую известен, то есть мы знаем, что
.
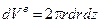В данном случае аналитическое вычисление интегралов и практическая реализация на ЭВМ может приводить к вычислению со значительной погрешностью, потому что после интегрирования получаются выражения вида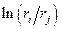 
. Для конечных элементов, расположенных далеко от оси вращения и маленьких по размеру 
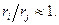Вычислять интеграл надо численно. Проще всего и достаточно точно можно применить одноточечное интегрирование:
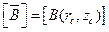, где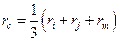 
, 
.
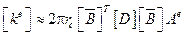, при измельчении сетки 
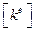стремится к точному значению.
L -координаты.
L -координаты – система трёх естественных для треугольника относительных координат.
.
.
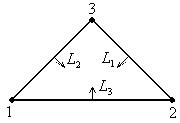
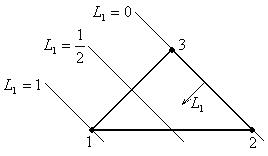
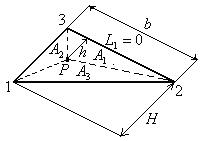
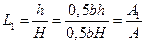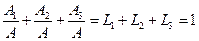При деформации элемента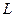 
-координаты не изменяются! По сути 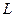-координаты удовлетворяют всем требованиям, предъявляемым к функциям формы, то есть их можно использовать в качестве функций формы элемента: 
!
.
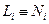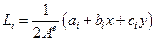Для L -координат установлены следующие соотношения:
,
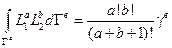, где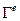 
– дуга стороны элемента, а 
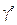её длина!
В этом случае вектор постоянных массовых сил для симплекс-элемента, например, можно вычислить следующим образом:
.
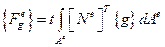В этот вектор будут входить интегралы вида:
.
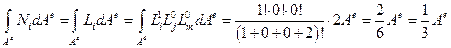Для постоянной распределённой по стороне нагрузки тоже можно записать подобные вычисления:
.
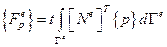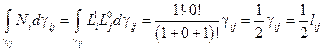, где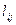 
– расстояние между 
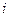и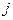 
узлами.
Треугольные конечные элементы с нелинейной Лагранжевой аппроксимацией
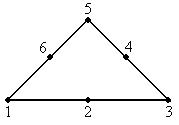
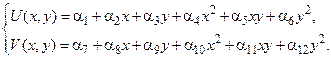
Такой конечный элемент называется квадратичным.
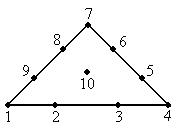
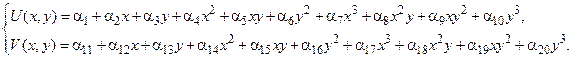
Такой конечный элемент называется кубическим.
Треугольник Паскаля: порядок аппроксимации на единицу меньше числа узлов на стороне треугольника.
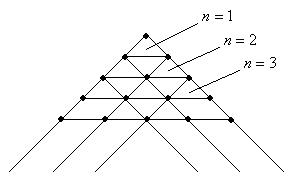
Явный способ построения функций форм треугольных элементов
,
где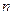 
– порядок аппроксимации; 
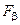– функции L -координат 
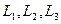, определяется из уравнений 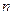линий, которые проходят через все узлы за исключением 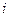-го узла, для которого определяется функция формы.
В знаменателе стоит значение функции 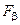в точке с координатами 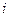-го узла.
Если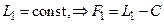 
.
Пример: получим функции формы для кубического элемента.
; 
.
; 
.
.
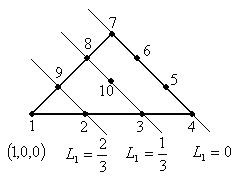
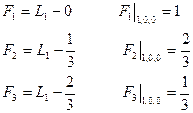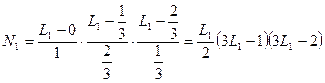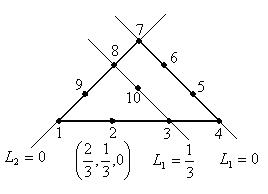
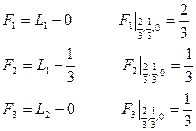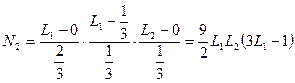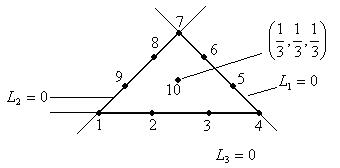
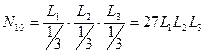Функции формы для кубического элемента:
;
; 
; 
; 
.
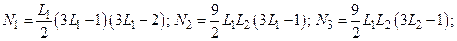
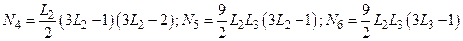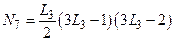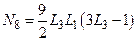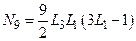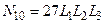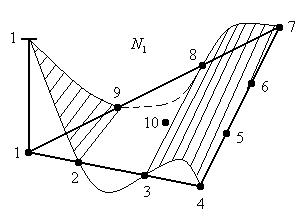
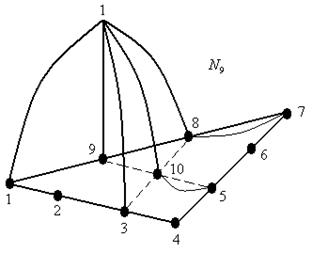
Таким образом, у таких конечных элементов первые производные от функции формы не постоянны, следует, напряжения и деформации изменяются в пределах конечного элемента, но несогласованны между конечными элементами.
«+» 1. требуется меньшее число нелинейных треугольников для получения той же точности, что и в симплекс-элементе.
2. возможно построение элементов с криволинейными границами.
«–» 1. так как больше узлов, значит больше координат.
2. более громоздки процедуры.