Идея метода Власова – Канторовича заключается в сведении решения двумерных задач изгиба пластин к системе обыкновенных дифференциальных уравнений от одной переменной. Неизвестные перемещения задачи задаются в виде суммы произведений двух функций, одни из которых задаются как функции одной координаты, а вторые являются неизвестными функциями другой координаты и находятся из решения вариационной задачи. Этот метод более точный, чем рассмотренные ранее, так как по искомому направлению решения задачи можно удовлетворять любые граничные условия. Согласно методу представим функцию прогиба в виде конечного ряда
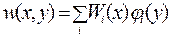(4.11)
Функции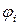 
являются аппроксимирующими, которые задаются так, чтобы были удовлетворены геометрические граничные условия. Для определения искомых функций 
используется вариационный принцип Лагранжа. Запишем полную энергию пластины в форме (4.3).
.
После подстановки в выражение энергии функции прогиба в форме (4.11) подынтегральное выражение примет вид
.
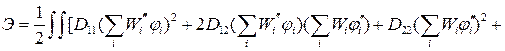
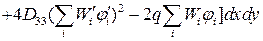Проинтегрировав выражение по координате y, подынтегральный функционал запишется в виде
,
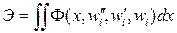А уравнение Эйлера-Лагранжа и естественные граничные условия запишутся
;
.
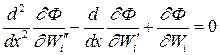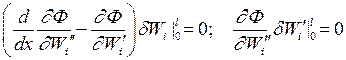После вычисления производных от функционала по искомым функциям уравнение Эйлера-Лагранжа примет вид
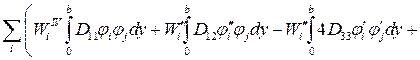
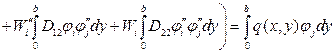. (4.12)
Учтя интегрирование по частям подынтегральных выражени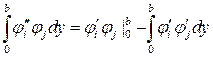й
и 
и объединяя одинаковые подынтегральные производные функций 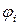при цилиндрических жесткостях 
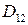и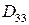 
, разрешающее дифференциальное уравнение запишется в виде
, (4.13)
где для ортотропной пластины введены обозначения:
; 
; 
; 
.
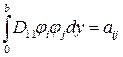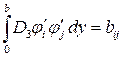Для пластины из ортотропного и изотропного материала в дифференциальном уравнении остаются только четные производные. В этом случае для определения корней характеристического уравнения мы получаем биквадратное алгебраическое уравнение.
Пример [5]. Рассмотрим консольно закрепленную по одной стороне пластину и введем безразмерные координаты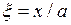 
, 
, 
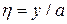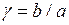(рис.4.3). Вдоль закрепленной стороны направим координату 
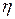(длина стороны 
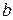). Логично задавать функции по координате 
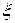, то есть функции 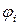, так как легко подобрать для решения балочную функцию в виде 
, которая удовлетворяет всем граничным условиям на закрепленной стороне и на свободном краю
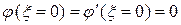и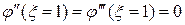 
.
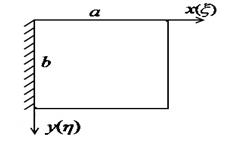
Рис.4.3. Рассчитываемая пластина
В качестве выбранной функции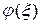 
можно принять решение дифференциальное уравнение изгиба балки 
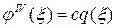. Будем считать, что пластина квадратная и 
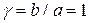, а нагрузку примем в виде 
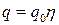. С учетом заданной функции решения 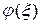разрешающее уравнение (4.13) можно переписать в виде
,
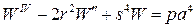где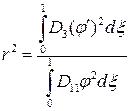 
; 
; 
.
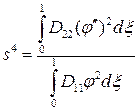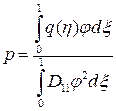Решение уравнения имеет вид
,
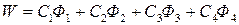где функции решения
, 
,
, 
,
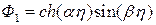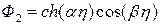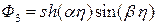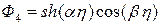а корни характеристического уравнения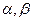 
равны
; 
.
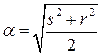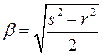Для изотропной квадратной пластины цилиндрические жесткости равны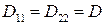 
; 
; 
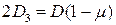, а дифференциальное уравнение примет вид
.
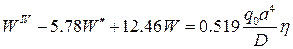Естественные граничные условия пр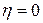и 
и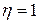 
записываются в виде
; 
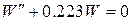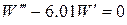. Из решения двух уравнений на границе находим постоянные 
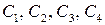. Окончательно для прогиба пластины получим выражение
.
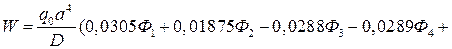
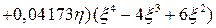Поверхность прогибов пластины показана на рис 4.4.
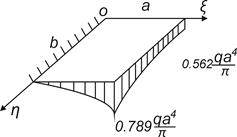
Рис.4.4. Результаты расчета