Умение составлять алгоритм включает в себя следующие умения:
· Выявлять способ действий;
· Выделять основные элементарные действия, из которых состоит данное;
· Планировать структуру выделенных действий;
· Умение организовать поиск данных;
· Умение правильно записывать алгоритм.
Умения предполагается формировать во II и III классах. Но в I классе целесообразно предлагать задания, способствующие формированию следующих умений:
Выявлять способ действия. Выявление способа решения задачи важно потому, что большинство предлагаемых в начальной школе задач имеет алгоритмическую структуру и очень часто достижение результата действий зависит от того, насколько решающий осознает ее.
Рассмотрим задачи, одной из целей, решения которых является выявление способа действия.
1. Даны числа (рис. 29). Составьте примеры. Вычислите:

Можно ли еще составить примеры на сложение? Если можно, то составьте. Сколько всего таких примеров на сложение можно составить? Как вы рассуждаете при составлении возможных примеров на сложение, чтобы не пропустить ни одного случая?
При выполнении этих заданий важно уяснить, что для того чтобы записать все возможные примеры, нужно придерживаться какого-то определенного способа образования их, например: фиксировать первое слагаемое – 51, а в качестве второго слагаемого перебирать все числа второго столбика, затем в качестве первого слагаемого фиксировать, например, 41 и опять перебирать все числа второго столбика и т. д.; можно фиксировать второе слагаемое и перебирать все числа первого столбика и т. д. Важно показать, что, придерживаясь какого-то определенного способа действия, мы не упустим ни одного случая и ни один из случаев не запишем дважды.
2. Сколькими способами можно повесить пальто на вешалке, имеющей 4 крючка? Как изменится ответ задач, если будут два различных пальто?
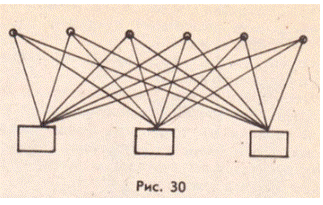
3. В зале 3 люстры и 6 окон. Для украшения к празднику от каждой люстры к каждому окну протянули гирлянду. Сколько всего повесили гирлянд? (Можно использовать схематический рис. 30.)
С целью выявления способа действий полезны комбинаторные задачи. Эти задачи обычно предполагают практическое выполнение. Особенность этих задач в том, что они имеют не одно, а множество решений и при их решении необходимо осуществлять перебор в рациональной последовательности.
Планировать структуру выделенных действий. Формированию этого умения способствуют задания на установление отношения «сначала - потом». Сюжетные картинки следует подбирать таким образом, чтобы их можно было использовать для составления задач.
Организовать поиск данных. Формированию этого умения способствует решение задач с недостающими данными, а также составление задач самими учащимися на основе справочных таблиц.
Таков один из возможных путей реализации в I классе логико-алгоритмической линии курса математики в начальной школе.
Во всех учебниках математики начальной школы кроме учебников
Л. Г. Петерсона 2 класс 1 ч. стр. 75 и Т. Е. Демидовой 2 класс 3 ч. стр. 66, в явном виде не дается определение алгоритма, но всегда можно обучать учащихся умению распознавать алгоритмы.
М2П 1 ч. Стр. 75-76


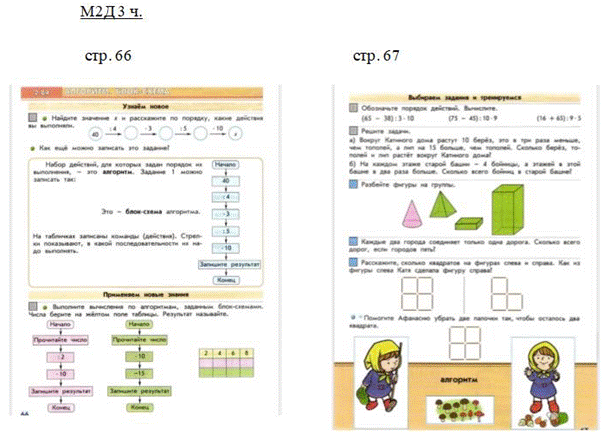
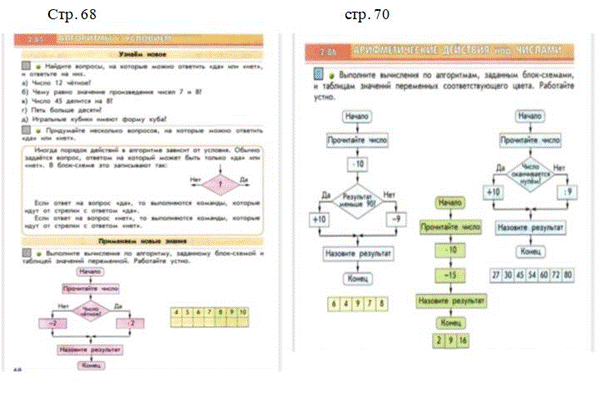
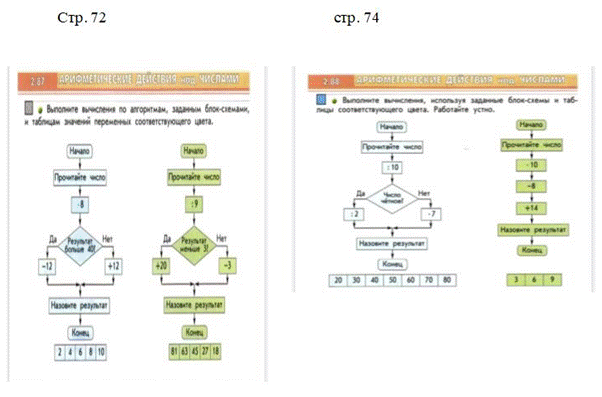
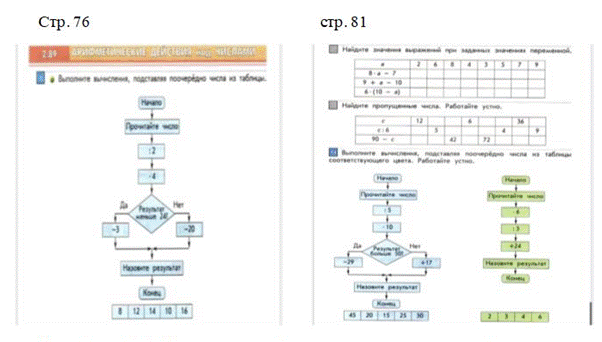
В учебнике А. Л. Чекина не дается, но в конце учебника 3 класс 1 ч. на странице 148 – 149 в словаре есть определение «алгоритм».

В учебнике И. И. Аргинской 3 класс 1 ч. дается только такое задание

Рассматриваются алгоритмы письменных вычислений с объяснением их выполнения по плану, задачи решаемые с конца.

Для этого можно предлагать учащимся предписания, в которых отсутствует какое-нибудь свойство алгоритма. Перечислим возможные случаи: 1.В предписании имеются непонятные исполнителю действия (отсутствует понятность). 2.Содержатся неточные действия (отсутствует определенность). 3.Перечень действий не завершен, отсутствует последняя команда, приводящая к решению задачи (отсутствует результативность). 4.Пропущено какое-то действие, кроме последнего, или нарушен порядок (отсутствует дискретность). 5.Число действий в предписании не ограничено (отсутствует конечность). 6. Предписание предназначена для решения одной конкретной задачи.(отсутствует массовость). 7.Предписание содержит сложные действия (отсутствует элементарность). Например: Выясните, является ли предписание алгоритмом, если нет, то определите какое свойство нарушено. Исправьте предписание. чтобы оно стало алгоритмом.
а) алгоритм построения отрезка определенной длины.
1.отметь в тетради карандашом точку.
2.приложи линейку к точке.
3.найти на линейке штрих, соответствующий заданной длине отрезка.
4.отметь в тетради точку напротив штриха.
5.соедините точки карандашом по линейке (в этом алгоритмическом предписании нарушена определенность, нужно во второй пункт добавить условие «так, чтобы штрих соответствовал нулю).
б) алгоритм построения отрезка определенной длины.
1.возьми карандаш и поставь в тетради точку.
2.приложи линейку к точке так, чтобы штрих. соответствующий нулю, совпадал с точкой.
3.Найди на линейке штрих, соответствующий 5 см.
4.поставь в тетради напротив этого штриха точку.
5.Соедини две точки карандашом по линейке.(В этом алгоритмическом предписании нарушена массовость. так как в третьем пункте уточняется длина отрезка- 5 см.)
в) алгоритм последовательности прибавления к однозначному числу чисел 1,2,3, и т.д.
1) запиши однозначное число
2) прибавь к нему 1, запиши результат.
3) к полученному результату прибавь 2, запиши результат.
4) к полученному результату прибавь 3, запиши результат (в этом алгоритмическом предписании отсутствует конечность).
Г) алгоритм нахождения площади квадрата (в нкм)
1) измерь сторону квадрата.
2) запиши значение длины, указав единицы измерения.
3) возведи знаменатель длины в квадрат.
4) запиши полученное значение площади в квадратных единицах измерения (отсутствует понятность, так как в нкм не преподается возведение числа в квадрат).
д) алгоритм посадки дерева
1)зарой яму
2) наполни ямку водой
3) возьми лейку
4) возьми лопату
5) полей дерево
6) вставь дерево в яму
7) вырой яму (отсутствует дискретность, нужно поменять местами первый и седьмой пункты).
Элементарные шаги алгоритма при укрупнении объединяются в алгоритмические конструкции: последовательные, ветвящиеся, циклические, рекурсивные. В 1969 году Эдсгер Вибе Дейкстра в статье «Структуры данных и алгоритмы» доказал, что для записи любого алгоритма достаточно трех основных алгоритмических конструкций: последовательных, ветвящихся, циклических.
Последовательный алгоритм (линейный) – это простейший по структуре алгоритм, в котором действие выполняются последовательно друг за другом. Например алгоритм получения настоя шиповника
1. измельчить плоды шиповника в ступке.
2.залить кипящей водой в пропорции 10 граммов плодов на стакан воды
3. кипятить 10 минут
4. охладить
5.процедить.
Разветвленный алгоритм - это алгоритм, в котором порядок действий зависти от выполнения некоторого условия (если, то). Примером разветвленного алгоритма является алгоритм письменного сложения.
Циклический - это алгоритм, в котором некоторые действия могут выполняться многократно. Примером циклического алгоритма является
алгоритм письменного сложения нескольких пар многозначных чисел (если еще есть пары, тогда алгоритм пошел, иначе – закончен).
При изучении алгоритмов важно осознать, что существует много разных возможностей для представления (описания) одного и того же алгоритма:
* текстовая форма записи;
*запись в виде блок – схемы;
*запись алгоритма на каком-либо алгоритмическом языке;
*представление алгоритма в виде машины Тьюринга или машины Поста.
При изучении математики у школьников формируются такие действия, как действия планирования своей деятельности, оценка ее результата, поиска плана решения задачи, чтения учебных текстов, и другие. Если все эти действия проанализировать, то можно составить алгоритмические предписания по их выполнению, а затем использовать как ориентиры для разных видов деятельности.
Например, алгоритмическое предписание анализа и поиска плана решения задачи может быть таким:
1.Прочитайте задачу и назовите процесс, о котором в ней идет речь.
2.Укажите величины, которые характеризуют этот процесс.
3. Выделите, что дано и что нужно найти в задаче.
4.Выясните, как связаны данные величины и те, которые требуются найти.
5. Подумайте, как на основании имеющихся у вас знаний о величинах, о которых идет речь, ответить на требования задачи.
6. Составьте план решения предполагаемой задачи.
Кроме общих учебных действий при изучении математики формируются действия, связанные с освоением конкретного материала. Многие из них носят алгоритмический характер, поэтому для овладения ими целесообразно оставлять предписания. В частности, к таким действиям относятся: усвоение нового определения понятия (правила, свойства, теоремы); распознавание принадлежности объекта объему данного понятия; нахождение значения переменной по формуле; решение однотипных задач и др.
Таким образом, обучение математике требует от учителя умения строить алгоритмические предписания.
Вопрос. Опишите методику обучения младших школьников решению комбинаторных задач. Какие способы решения комбинаторных задач вам известны из курса математики? Какими способами решения этих задач могут воспользоваться учащиеся начальных классов? Приведите примеры.
Для формирования у учащихся умения выявлять способ действия полезны комбинаторные задания. Их особенность в том, что они имеют не одно, а множество решений, и при их выполнении необходимо осуществлять перебор в рациональной последовательности.
Комбинаторика - раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
В обучении школьников решению комбинаторных задач соблюдается этапность.
Первый этап – подготовительный. На этом этапе учащиеся приобретают опыт образования объектов из отдельных элементов. Новые объекты ученики составляют, осуществляя хаотичный перебор, и от них не требуется найти все возможные варианты в данной задаче.
Учащиеся также знакомятся с новым методом решения задач. На комбинаторных задачах идет обучение методу перебора, который можно в дальнейшем использовать и для решения другого типа задач.
Кроме того целенаправленное обучение решению комбинаторных задач способствует развитию такого качества мышления, как вариативност ь. Под вариативностью мышления мы понимаем направленность мыслительной деятельности ученика на поиск различных решений задачи в случае, когда нет специального указания на это.
Комбинаторные задачи отбирались нами, во-первых, адекватно выбранному методу (методу перебора), во-вторых, с учетом возрастных психологических особенностей детей. Поясним подробнее эти положения.
Итак, подбирались такие комбинаторные задачи, решение которых можно осуществлять методом перебора. Среди них были задачи разные по сложности осуществления перебора. По этому признаку мы разделили их на три группы:
1. Задачи, в которых нужно произвести полный перебор всех возможных вариантов.
2. Задачи, в которых использовать прием полного перебора не целесообразно и нужно сразу исключить некоторые варианты, не рассматривая их (т. е. осуществить сокращенный перебор).
3. Задачи, в которых операция перебора производится несколько раз и по отношению к разного рода объектам.
Приведем примеры таких задач:
1. Расставляя знаки «+» и «—» между данными числами 9...2...4, составь все возможные выражения.
Проводится полный перебор вариантов:
1) два знака в выражении могут быть одинаковыми, 9+2+4; 9-2-4;
2) два знака могут быть разными, тогда получаем 9+2-4, 9-2+4. (Затем можно предложить детям найти значения составленных выражений.
2. Учитель говорит, что он нарисовал в ряд 4 фигуры: большой и маленький квадраты, большой и маленький круги так, что на первом месте находится круг и одинаковые по форме фигуры не стоят рядом, и предлагает ученикам отгадать, в какой последовательности расставлены эти фигуры. Всего существует 24 различных расположения этих фигур. И составлять их все, а потом выбирать соответствующие данному условию не целесообразно, поэтому проводится сокращенный перебор:
на первом месте может стоять большой круг, тогда маленький круг может быть только на третьем месте, при этом большой и маленький квадраты можно поставить двумя способами - на второе и четвертое место (рис.1).
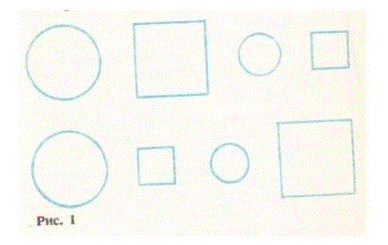
Аналогичное рассуждение проводится, если на первом месте стоит маленький круг, и также составляются два варианта (рис. 2).
Составляя эти варианты, ученики находят тот, который был задуман учителем.
3. Три компаньона одной фирмы хранят ценные бумаги в сейфе, на котором 3 замка. Компаньоны хотят распределить между собой ключи от замков так, чтобы сейф мог открываться только в присутствии хотя бы двух компаньонов, но не одного. Как это можно сделать?
Сначала перебираются все возможные случаи распределения ключей. Каждому компаньону можно дать по одному ключу или по два разных ключа, или по три.
Предположим, что у каждого компаньона по одному ключу. Тогда, если придут любые двое из них, то они не смогут открыть сейф.
Предположим, что у каждого компаньона по три разных ключа. Тогда сейф сможет открыть один компаньон, а это не соответствует условию.
Дадим каждому компаньону по два разных ключа. Первому -1 и 2 ключи, второму — 1 и 3 ключи, третьему - 2 и 3 ключи. (Осуществляется выбор из трех типов ключей по два ключа). Проверим, когда придут любые два компаньона, смогут ли они открыть сейф. Рассматриваются все возможные случаи.
Могут прийти первый и второй компаньоны, у них будут все ключи (1 и 2, 1 и 3 ключи). Могут прийти первый и третий компаньоны, у них также будут все ключи (1 и 2, 2 и 3). Наконец, могут прийти второй и третий компаньоны, у них тоже будут все ключи (1 и 3, 2 и 3).
Таким образом, чтобы найти ответ в этой задаче, нужно выполнить операцию перебора несколько раз.
Комбинаторные задачи, решаемые методом перебора, подбирались нами так, чтобы совокупность этих задач удовлетворяла принципу полноты. Включались основные виды комбинаторных задач: на упорядочение элементов множества, на выбор подмножеств и их упорядочение, на выбор подмножеств. Разнообразные задачи в каждой группе мы получали благодаря варьированию числа объектов, самих объектов, наличия дополнительных условий, повторяющихся элементов, способов упорядочения (слева направо, сверху вниз, по кругу и т. д.).
Приведем примеры некоторых задач:
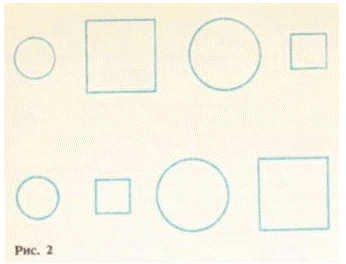
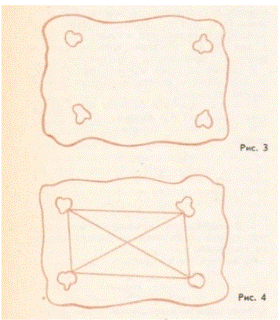
1. Задача на упорядочение предметов (по кругу), среди которых есть одинаковые: «Нарисуй, какие различные колечки можно сделать из 5 одинаковых маленьких бусинок и 2 одинаковых больших бусинок».
Ответ изображен на рисунке 3.
2. Задача на выбор подмножеств и их упорядочение (слева направо) при наличии дополнительных условий: «Запиши все двузначные числа, которые можно составить из цифр 2, 4, 7 и 8, так чтобы число десятков было больше числа единиц».
Ответ: можно составить шесть чисел: 42, 72, 74, 82, 84, 87.
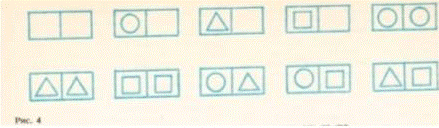
3. Задача на выбор по одному, по два из трех элементов с повторениями: «Сделай карточки для игры в геометрическое домино, используя 3 фигуры: круг, квадрат и треугольник».
Ответ: изображен на рисунке 4.
Также подбирались задачи, различающиеся по характеру содержащегося в них требования:
1. Задачи, в которых требуется найти и сосчитать, сколько всего можно составить различных вариантов.
2. Задачи, в которых требуется выяснить, существует ли определенная комбинаторная конфигурация, отвечающая поставленным условиям.
3. Задачи, в которых нужно найти и выбрать наилучший вариант по определенным критериям.
Все рассмотренные выше задачи являются перечислительными. Приведем примеры задач двух других видов:
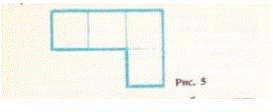
1. Из прямоугольного листа бумаги длиной 7 см и шириной 4 см нужно вырезать 7 одинаковых деталей, таких, как рисунок 5. Можно ли это сделать?
Ответ: нельзя расположить 7 таких деталей в данном прямоугольнике.
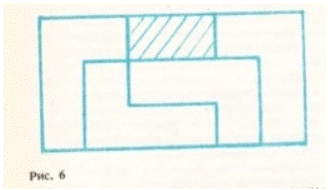
2. Из прямоугольного листа бумаги длиной 6 см и шириной 3 см нужно вырезать одинаковые детали, такие, как рисунок 5. Нарисуй, как расположить эти детали, чтобы получить их из этого листа как больше.
Ответ изображен на рисунке 6
Наряду с описанными задачами включаются и обратные комбинаторные задачи, например: «В одном очень маленьком городе всего 10 различных маршрутов трамвая. Чтобы жители города вечером могли издалека определить номер трамвая, было решено сделать различные цветные огоньки для каждого маршрута. Но десяти стекол различных цветов не нашли. Стекла оказались только четырех цветов: красного, синего, желтого и зеленого. Как же можно выполнить задуманное?»
Эта задача также решается методом перебора. Сначала учащиеся пробуют обозначить каждый маршрут, используя по два разноцветных огонька:
кс кж кз сж сз жз
ск жк зк жс зс зж
Но варианты первого и второго рядов, расположенные друг под другом, можно перепутать, поэтому нужно взять только 6 этих обозначений, а остальные 4 маршрута обозначить одним огоньком, например, так:
1-й - кс, 2-й - кж, 3-й - кз, 4-й - сж,
5-й - сз, 6-й - жз,7-й - к,8-Й - с,
9-й – ж, 10-й - з.
При отборе задач учитывались также психологические особенности младших школьников. Исходя из того, что у детей данного возраста еще сохраняется тесная связь мышления с практическими действиями, система задач составлялась таким образом, чтобы обеспечить постепенный переход от манипуляции с предметами к действиям в уме.
Преобразования можно производить реально или идеально (мысленно), с реальными предметами или знаково-символическими объектами, с опорой на
запись или без нее. Мы идем от реальных преобразований с реальными предметами с опорой на запись к идеальным преобразованиям знаково-символических объектов с опорой на запись (возможно выполнение запись, но добиваться этого от детей нецелесообразно).
Приведем некоторые примеры.
1. В воскресенье трое друзей (Маша, Саша, Дима) решили пойти в парк. Они пришли к аттракциону «Автодром». По правилам на одну машину садятся двое: водитель и пассажир. Чтобы никому не было обидно, ребята решили: каждый должен побывать водителем и каждый должен покататься одинаковое число раз. Какое решение они нашли?
Ответ: составляются следующие пары:
Маша — Саша, Саша — Дима, Дима — Маша (имя водителя подчеркнуто).
В данной задаче есть возможность прийти к решению, разыгрывая сценку с детьми и выполняя таким образом реальные преобразования с реальными объектами.
2. Переставляя только числа, составь все возможные выражения: 10+8-9.
Ответ: 10+9-8, 8+9-10, 8+10-9, 9+8-10, 9+10-8. связь или знаково-символическими и без опоры на запись, но добиваться этого от детей нецелесообразно).
Решая эту задачу, ученики выполняют мысленно преобразования со знаково-символическими объектами.
При отборе задач обращалось внимание на тематику и форму представления этих задач. Мы старались, чтобы задачи не выглядели искусственными, а были понятны и интересны детям, вызывали у них положительные эмоции. Когда это было возможно, для составления задач использовали практический материал из жизни. В других случаях задачи предлагали детям в виде разнообразных игр.
Второй этап. Обучение школьников решению задач с использованием систематического перебора.
Учащиеся начальных классов вполне могут решать комбинаторные задачи без использования формул случайным образом или с помощью приемов систематического перебора. Одним из первых встает вопрос проблематики таких задач.
Рассмотрим сначала то, что уже разработано и используется.
Анализ комбинаторных задач, составленных для учащихся младших классов, показывает, что большая часть их тесно связана с основным содержанием курса математики.
Например:
1. Запиши все возможные трехзначные числа, используя цифры 1,2, 3.
2. Запиши различные разности, которые можно составить из чисел 50, 27, 45, 13, если для составления разностей брать по два числа. Вычисли значение разностей.
3. Сколько прямоугольников изображено на рисунке 1?

В каждом случае решается своя учебная задача: в первом случае - усвоение позиционного принципа записи чисел, во втором - формирование вычислительных навыков и в третьем - формирование умения выделять прямоугольники на чертеже. Поэтому мы считаем нецелесообразным обучение приемам систематического перебора на заданиях особого вида. Их основная цель должна состоять в том, чтобы помочь учащимся открыть приемы, с помощью которых можно было бы не пропускать и не повторять несколько раз одни и те же варианты, как это часто происходит при случайном переборе. В данной статье приведены примеры таких задач и описана работа с ними.
Первые комбинаторные задачи должны давать возможность выполнять практические действия, которые потом будут перенесены в план умственных действий, например: сколькими способами можно положить в ряд ручку, карандаш и резинку? Недостатком подобных задач является то, что учащиеся не понимают целесообразности их решения. Для обеспечения мотивации таких задач мы предлагаем их в виде игр. Также, когда это возможно, используем для составления задач практический материал из жизни.
Опишем сначала некоторые задачи-игры.
Игра «День – ночь»
Учитель вызывает трех учеников (например, Наташу, Сережу, Борю). Они садятся у доски на стулья. По команде «День!» ребята встают и могут передвигаться. По команде «Ночь!» они садятся на стулья, но так, чтобы каждый раз порядок расположения их был другой. Все остальные дети записывают в тетради расположение вызванных учеников по первым буквам имен и следят за тем, чтобы играющие выполняли поставленное условие. Игра продолжается до тех пор, пока не обнаружатся все возможные варианты. Их шесть:
l. Н. С. Б.
2. С. Н. Б.
3. Б. Н. С.
4. Н. Б. С.
5. С. Б. Н.
6. Б. С. Н.
В процессе игры возникают ситуации, когда играющие повторяют расположение или не могут найти новое. Тогда им помогают ребята из класса. Возникают вопросы: «Можно ли играть без ошибок? Как нужно действовать для этого?» Ученики осознают необходимость введения правила, которого надо придерживаться в игре. Анализируя полученные расположения, они замечают, что нужно каждому садиться на первое место дважды, а двум остальным при этом меняться местами.
Игра в парах
У каждой пары играющих - набор деревянных или картонных моделей фигур: треугольника, круга и квадрата. Первый ученик расставляет модели фигур в ряд в любом порядке и зарисовывает их расположение на листе бумаги. Второй меняет расположение и зарисовывает свой вариант. И, таким образом, по очереди каждый переставляет модели фигур, но так, чтобы не было одинаковых расположений. Следить за выполнением этого условия позволяют записи сделанных ходов. Проигрывает тот, кто повторяет или не может составить новый набор, когда это возможно. Игра заканчивается, если все варианты составлены. Выиграть помогает правило, выведенное в первой задаче (если на первом месте треугольник, то, круг и квадрат можно разместить двумя способами, меняя их местами. Если на первое место поставить круг, то треугольник и квадрат также размещаются двумя способами. И наконец, на первое место нужно поставить квадрат и разместить круг и треугольник двумя способами).
Игра «Башенки»
Учитель кладет в коробку три кубика: красного, синего и желтого цвета. И говорит, что будет брать, не глядя, по одному кубику и составлять башенку следующим образом: первый кубик - нижний этаж, второй - средний, третий - верхний. Детям предлагается задумать вариант башенки, которая может получиться, и нарисовать его, изображая кубики квадратами соответствующего цвета. Затем проводится опыт (кубики вынимаются из коробки). Тот, кто угадал результат опыта, становится победителем. Игру можно повторить несколько раз. В результате ученики приходят к выводу, что если рисуешь одну башенку, то моешь получить в опыте как задуманный, так и другой порядок цветов. Возникает задача: «Сколько же башенок надо нарисовать, чтобы быть уверенным, что, сколько бы опытов мы ни проводили, среди рисунков всегда окажется нужный и ты постоянно будешь выигрывать?»
Таким образом, правила игры несколько изменяются. Можно задумать не один вариант расположения кубиков. Дети стараются нарисовать все башенки, которые можно составить. Должно получиться шесть рисунков:

Проводятся опыты. И тот, кто составил все варианты, выигрывает.
В процессе решения данной задачи учащиеся осуществляют перенос наглядного приема, используемого в задачах 1 и 2, в мысленную сферу. Чтобы составить все варианты башенок, они должны повторить в уме те же действия, которые раньше выполняли практически с предметами.
В описанных играх можно изменять различным образом данные и получать новые задачи, например:
l. Для составления башенок взять 4 кубика: l красный и 3 желтых.
В этом случае возможны четыре варианта:

2. В коробку положить 1 красный и 2 желтых кубика, а башенки составлять только из 2 кубиков.
Возможны три варианта:

Итак, одно из направлений это задачи игры. Другое - задачи, показывающие некоторые доступные детям аспекты применения комбинаторики в повседневной деятельности человека, например:
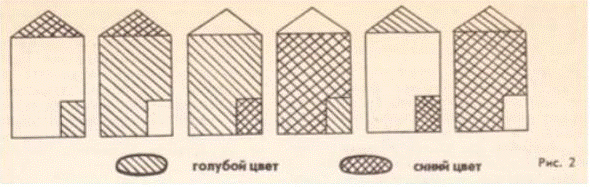
l. Малярам нужно покрасить 6 дачных домиков для малышей детского сада (красят крышу, стены и дверь). У них есть синяя, голубая и белая краски. Могут ли маляры покрасить все дома по-разному, чтобы малыши по цвету узнавали свой дом? Учащимся предлагается нарисовать 6 домиков, взять цветные карандаши и показать, как нужно выполнить работу маляра. Ответ изображен на рисунке 2.
2. В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т. е. не нужно было идти в обход. Покажи, какие дорожки (рис. 3) будут сделаны.
Ответ изображен на рисунке 4
3. Художественный бланк телеграммы стоит 15 к., за доставку надо заплатить 25 к. Если телеграмма не срочная, то за каждое слово платят 6 к., если срочная, то за слово платят 25 к. Какую телеграмму можно отправить, если есть 5 р. 30 к. и текст, состоит из 20 слов?
А если есть только l р. 50 к.?
Для решения данной задачи необходимо иметь и комбинаторные, и вычислительные умения. Сначала определяют, какие виды телеграмм возможны: срочная на художественном бланке, срочная на обыкновенном бланке, не срочная на художественном бланке, не срочная на обыкновенном бланке. Затем подсчитывают стоимость телеграммы в каждом случае и сравнивают с числом имеющихся денег.
4. У кассы кинотеатра стоят четверо ребят. У двух из них рубли у других двух полтинники. (Учитель вызывает 4 учеников к доске и дает им модели монет.) Билет в кино стоит 50 к. В начале продажи касса пуста. (Учитель вызывает «кассира» и дает ему «билеты».) Затем формулируется задача: «Как должны расположиться ребята, чтобы никому не пришлось, ждать сдачи?»
Разыгрывая сценку, ученики находят два возможных варианта:
а) 50 к., 1 р., 50 к., 1 р.
б) 50 к., 50 к., l р., l р.
Затем предлагается решить: «Что произойдет в том случае, когда у двоих полтинники, а у троих рубли? (В этом случае одному человеку кассир не сможет дать сдачи.)
По сложности осуществления перебора задачи повышенной трудности делятся на следующие группы:
1. Задачи, в которых нужно произвести полный перебор во всех возможных вариантах.
Пример задачи. Расставьте знаки «+» и «-» между данными числами 9…2…4, составьте все возможные выражения.
Способ решения задачи – проводится полный перебор вариантов (используется прием полной индукции).
Варианты решения. 9+2+4, 9-2-4, 9-2+4, 9+2-4.
2. Задачи, в которых производится сокращенный перебор вариантов из-за нецелесообразности выполнения полного перебора.
Пример задачи. Четыре фигуры нарисованы в ряд: большой и маленький квадраты, большой и маленький круги так, что на первом месте находится круг и одинаковые по форме фигуры не стоят рядом. Отгадайте последовательность рассматриваемых фигур.
Способ решения задачи – всего существует 24 различных вариантов расположения этих фигур и составлять их все, а потом выбирать соответствующие данному условию нецелесообразно, поэтому проводится сокращенный перебор вариантов, удовлетворяющих условию задачи.
Варианты решения:
Большой круг – большой квадрат – маленький круг – маленький квадрат.
Большой круг – маленький квадрат – маленький круг – большой квадрат.
Маленький круг – большой квадрат – большой круг – маленький квадрат.
Маленький круг – маленький квадрат – большой круг – большой квадрат.
3. Задачи, в которых операция перебора производится несколько раз, но по отношению к разного рода объектам.
Пример задачи. Три компаньона одной фирмы хранят ценные бумаги в сейфе, на котором три замка. Компаньоны хотят распределить между собой ключи от замков так, чтобы сейф мог открываться в присутствии двух компаньонов, но не одного. Как это можно сделать?
Способ решения задачи. Сначала перебираются все возможные случаи распределения ключей. Каждому компаньону можно дать по 1 ключу или по 2 ключа, или по 3 ключа. Потом выбранный вариант проверяется в разных ситуациях.
Варианты решения. Для записи решения задачи можно выбрать различные способы обозначения ключей (заместителей реальных предметов).
При отборе комбинаторных задач важно учитывать следующие условия:
1. Совокупность задач должна удовлетворять принципу полноты.
С этой точки зрения необходимо в работе над комбинаторными задачами использовать следующие основные виды комбинаторных задач:
- на упорядочение элементов множества,
- на выбор подмножеств и их упорядочение,
- на выбор подмножеств.
2. Необходимо учитывать характер содержащегося в них требования.
С этой точки зрения можно выделить следующие группы задач:
- Задачи, в которых требуется найти и сосчитать, сколько всего можно составить различных вариантов;
- Задачи, в которых требуется выяснить, существует ли определенная конфигурация, отвечающая поставленным условиям;
- Задачи, в которых нужно найти и выбрать наилучший вариант по определенным критериям.
Задача на упорядочение предметов (по кругу), среди которых есть одинаковые.
Нарисуй, какие различные колечки можно сделать из 5 одинаковых маленьких бусинок и 2 одинаковых больших бусинок.
Задача на выбор подмножеств и их упорядочение (слева направо) при наличии дополнительных условий.
Запиши все двузначные числа, которые можно составить из цифр 2, 4, 7 так, чтобы число десятков было больше числа единиц.
Задача на выбор подмножеств и их подсчет их элементов.
Красная шапочка несла бабушке 14 пирожков: с мясом, с грибами и с капустой. Пирожков с капустой было наибольшее количество. Причем их вдвое больше, чем пирожков с мясом. Сколько пирожков с грибами?
Задача, в которой требуется найти и сосчитать, сколько всего можно составить различных вариантов.
Площадь прямоугольника равна 12 кв. см. Длины его сторон выражена целыми числами. Сколько различных прямоугольников можно построить согласно этим условиям?
Задача, в которой нужно найти один наилучший вариант, соответствующий определенным условиям.
В трехзначном нечетном числе сумма цифр равна 3. Известно, что все цифры различные. Найди это число.
Рассмотрение комбинаторных задач и различных возможностей их решения обеспечивают ученику выбор путей и средств решения в соответствии с индивидуальными особенностями.
Третий этап. Обучение школьников решению задач с использованием систематического перебора с использованием средств организации перебора.
Работа с графическими средствами отнесена на третий этап, так как, во-первых, при решении задач с небольшим числом элементов нет необходимости их использования, во-вторых, «язык» графов и таблиц не совсем прост и понятен детям, вследствие чего требуется специальное ознакомление с ними.
Прием графического и предметного моделирования является важным средством решения задач повышенной трудности.
Моделирование в широком смысле этого слова – замена действий с реальными предметами и действия с их образцами, моделями, муляжами, макетами, а также с графическими заменителями: рисунками, чертежами (с соблюдением масштаба), схемами (без точного соблюдения масштаба).
Предметное и графическое моделирование математической ситуации при решении задач давно применяется в школьной практике. Значение наглядности как средства развития более сложных форм конкретного мышления и формирования математических понятий состоит в том, что, как отмечает Л.Ш. Левенберг, «рисунки, схемы и чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать более рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их».
Таблица – это тоже модель задачи, но более абстрактная, чем схематический рисунок или чертеж.
Моделирование условия задачи повышенной трудности является одним из эффективных путей решения поиска решения, отражает глубину и полноту анализа связей, данных в задаче и, следовательно. Помогает ученикам успешно решить ее.
Обучение моделированию условия задачи включает ряд этапов:
1. Первоначально текст задачи повышенной трудности выписывается на доске и коллективно анализируется. Каждое предложение детей обсуждается и доказывается. В результате чего получается графическое изображение задачи.
2. Использование моделирования условий задач при работе с текстами задач разного вида сначала коллективно, а затем индивидуально.
3. Ознакомление учеников с разными способами моделирование, предоставление право выбора способа.
4. Обучение самостоятельному решения задач на основе выбранного ребенком самостоятельно способа решения.
Сначала как с наиболее простым средством организации перебора учащиеся знакомятся с таблицами. Рассматривая таблицу (рис.1), ученики «открывают» принцип ее составления. Затем им предлагается заполнить
другую таблицу. Проговариваются разные способы заполнения: по строчкам, по столбцам.
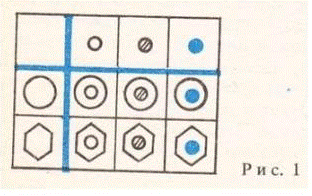
В дальнейшем в целях освоения принципа составления таблиц используются и такие задания:
1. Запиши в нужные клетки таблицы (рис.2) следующие числа: 57, 75, 44, 74, 55, 77, 47. Какие числа нужно