О: Полярной системой координат называется совокупность т. О (полюса) и выходящей из этой точки направленной полупрямой 
(полярной оси). Полярными координатами т.М называются числа 
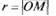(полярный радиус) и 
(полярный угол) (рис. 1, а).
Рис. 1
Если считать, что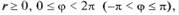 
то между точками плоскости и парами чисел 
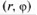устанавливается взаимно однозначное соответствие.
Пусть начало прямоугольной системы координат ХОY совпадает с полюсом, а положительная часть оси ОХ- с полярной осью. Тогда зависимость между координатами т.М в декартовой и полярной системах определяется формулами (рис. 1, б).
(1)
При нахождении 
необходимо учитывать, в какой четверти находится т. М, так как формулы (18.1) дают два значения полярного угла от 0 до 
Линия в полярной системе координат определяется уравнением 
Например, r = a, a = const - уравнение окружности с центром в полюсе и радиусом а (рис. 2, а);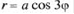 
- уравнение так называемой трехлепестковой розы (рис. 2, б).
Рис. 2
О: Криволинейным сектором в полярной системе координат называется фигура D с границей 
(рис. 1, а).
Для вычисления площади криволинейного сектора разобьем его на п частей лучами 
Пусть
- длина некоторого радиус-вектора, расположенного в 
(рис. 3, б).
Рис. 3
Площадь «ступенчатого» сектора, состоящего из п круговых секторов с центральными углами 
и радиусами 
За площадь криволинейного сектора естественно принять
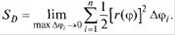
Так как в правой части этого уравнения стоит интегральная сумма для функции 
на отрезке 
то окончательно
имеем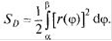 
Пример: Вычислить площадь, ограниченную трехлепестко-вой розой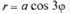 
(см. рис. 2, б).
Достаточно вычислить площадь половины одного лепестка при 
тогда
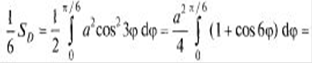
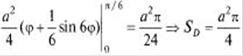
Пример: Найти площадь фигуры, ограниченной графиком функции y = xα, α > 0, прямой х = 1 и осью Ох. Решение. По формуле имеем
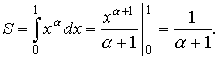
Пусть на отрезке [а, b] заданы две непрерывные функции y1 = f1(x) и y2 = f2(x), причем при всех значениях х из этого отрезка y1 ≤ y2. Найдем площадь фигуры, ограниченной графиками этих функций, а также прямыми х = а и х = b. Если обе функции неотрицательны, то площадь данной фигуры равна разности площадей криволинейных трапеций, ограниченных соответственно графиками функций y2 = f2(x), y1 = f1(x), прямыми х = а и х = b и осью абсцисс. Следовательно, площадь S данной фигуры можно найти так
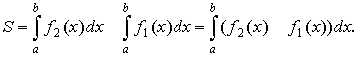
Вычисление объема тела по площадям параллельных сечений. Площадь сечения тела плоскостью перпендикулярной оси ОХ
. Рассмотрим некоторое тело Т (рис. 4), которое проектируется на ось ох в отрезок [a, b]. Пусть известна площадь любого сечения этого тела плоскостью, перпендикулярной оси ох. Величина площади является функцией от х: s = s (х).
определенный интеграл координата сечение
Рис. 4
Предположим, что s(х) - непрерывная функция, и приступим к вычислению объёма данного тела. Разобьём тело на слои плоскостями x = xi, перпендикулярными оси ох, и каждый слой заменим цилиндром (не обязательно круговым), высота которого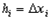 
, и основание 
, где 
- произвольная точка на [xi-1, xi]. Объём полученного ступенчатого тела
.
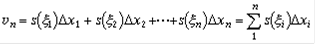Предел этой суммы при 
и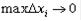 
равен объёму данного тела 
.
Так как s(х) - непрерывная функция на [a, b], то предел данной интегральной суммы существует и выражается определённым интегралом
. (22)
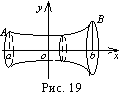
Рис. 5
. Пусть теперь тело образовано вращением вокруг оси ох криволинейной трапеции аАВb, ограниченной кривой у = f (х), осью ох и прямыми х = а, х = b (см. рис. 19). В этом случае произвольное сечение тела плоскостью, перпендикулярной оси ох, есть круг, площадь которого 
(радиус круга равен ординате точки).
Подставляя значение s(х) в формулу (22), получим:
. (23)
Замечание. Если тело образовано вращением кривой вокруг оси оу, c < y < d, то уравнение кривой следует записать в виде 
и использовать формулу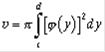 
.
Понятие интеграла может быть использовано для доказательства формул объемов тел: наклонной призмы, пирамиды, конуса шара и др. На рисунке изображено тело, объем которого необходимо вычислить. Предположим, что данное тело заключено между параллельными плоскостями х = а и х = b. Введен систему координат так, чтобы ось абсцисс была перпендикулярна этим плоскостям. Обозначим через S(х) площадь сечения тела плоскостью, перпендикулярной оси абсцисс и пересекающей ее в точке х, функция S(х) непрерывна на отрезке [а, b].
Рис. 6
Разделим отрезок [а; b] на n равных отрезков точками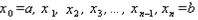 
и через точки деления проведем плоскости, перпендикулярные оси Oх. Эти плоскости разрезают заданное тело на n слоев. На рисунке тангирно выделен один из таких слоев. Тогда 
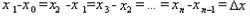. Если сечение тела есть круг, то объем заштрихованного слоя равен приближенно объему прямого кругового цилиндра с площадью основания S(х) и высотой Δx. Если сечение тела - многоугольник, то объем слоя равен приближенно объему соответствующей прямой призмы. Объем данного тела приближенно равен сумме объемов цилиндров или призм с основаниями 
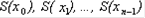и высотой Δx.
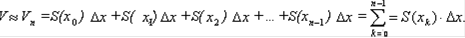
Точность этого приближённого равенства тем выше, чем больше n, т.е. тоньше слои. Примем без строгого обоснования, что объём данного тела равен пределу объёма 
Сумма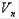 
является интегральной суммой для непрерывной на отрезке [a;b] функции S(x), следовательно, 