Урок-лекция
Тема урока: « Математическое ожидание и дисперсия случайной величины »
Цели урока:
- познакомить учащихся с основными числовыми характеристиками случайных величин: математическим ожиданием, дисперсией, средним квадратическим отклонением;
- рассмотреть свойства математического ожидания, дисперсии.
ХОД УРОКА
I. Изучение нового материала
Закон распределения полностью определяет случайную величину, однако, не всегда его возможно привести в полном объеме.
Для решения многих проблем достаточно знания отдельных числовых параметров, характеризующих наиболее существенные черты случайной величины. С помощью таких характеристик во многих случаях удается исследовать поведение случайных величин.
Основными числовыми характеристиками случайной величины являются:
- математическое ожидание;
- дисперсия;
- среднее квадратическое отклонение.
Рассмотрим эти характеристики для дискретной случайной величины.
Математическое ожидание
Определение: Математическое ожидание ДСВ находится по формуле:
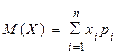
Вероятностный смысл этого выражения таков: при большом числе измерений среднее значение наблюдаемых значений величины Х приближается к ее математическому ожиданию.
Механический смысл этого равенства заключается в следующем: математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы - их вероятностям.
Пример 1. Закон распределения вероятностей дискретной случайной величины дан в виде таблицы. Найти математическое ожидание этой величины.
| Х | – 4 | – 3 | – 2 | – 1 | |||||
| Р | 0,02 | 0,03 | 0,1 | 0,15 | 0,4 | 0,15 | 0,1 | 0,03 | 0,02 |
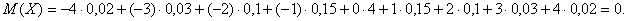
Математическое ожидание находят для однородных величин.
Свойства математического ожидания
- Математическое ожидание постоянной величины равно самой этой величине M (C) = C
- Постоянный множитель можно выносить за знак математического ожидания M (CX) = CM (X)
- Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий M (XY) = M (X) . M (Y)
- Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий M (X + Y) = M (X) + M (Y)
Пример.
Производится 3 выстрела с вероятностями p 1 = 0,4; p 2 = 0,3; p 3 = 0,6. Найти математическое ожидание общего числа попаданий, если:
| X 1 | X 2 | X 3 | ||||||
| P 1 | 0,4 | 0,6 | P 2 | 0,3 | 0,7 | P 3 | 0,6 | 0,4. |
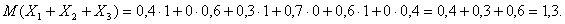
Пример. Найти математическое ожидание случайной величины (4 Х + 5) если М (Х) = 2.
М (4 Х + 5 ) = М (4 Х) + М (5) = 4М (Х) + 5 = 4 . 2 + 5 = 13
Дисперсия
Случайные величины могут иметь одинаковые математические ожидания, но различные возможные значения.
Например
| X | – 100 | Y | – 0,001 | 0,001 | |||
| P | 0,5 | 0,5 | P | 0,5 | 0,5 | ||
| M (X) = 0 | M (Y) = 0 |
Математические ожидания равны.
Возможные значения Y близки к M (Y) возможные значения Х далеки от своего M (X) то есть для характеристики случайной величины математического ожидания недостаточно, нужна характеристика рассеивания, т.е. разброса значений случайной величины, например в артиллерии важно насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.
Наиболее полной характеристикой разброса чисел является набор их отклонений от математического ожидания. Но когда набор чисел велик, рассматривать набор отклонений практически неудобно. Нужно описать разнообразие чисел в наборе одной характеристикой, одним числом.
Размах – слишком грубая мера разброса чисел в наборе, поскольку учитывает только два из них – наименьшее и наибольшее. Можно попробовать взять «среднее отклонение».
Для любого набора, если только не все числа в нем равны, часть отклонений будет положительна, а часть отрицательна. При этом сумма отклонений равна 0.
В этом состоит основное свойство отклонений: сумма отклонений чисел от математического ожидания этих чисел равна нулю.
Сумма отклонений всегда равна нулю, поэтому среднее арифметическое отклонений тоже равна нулю и его нельзя использовать как меру разброса.
Чтобы судить о разбросе, принято складывать не сами отклонения, а их квадраты. Квадраты отклонений неотрицательны, поэтому сумма квадратов отклонений зависит только от абсолютных величин отклонений, а не от их знаков. Чем больше отклонения чисел от математического ожидания, тем больше будет сумма квадратов отклонений. Для того, чтобы мера разброса чисел не зависела от их количества в наборе, в качестве такой меры берут среднее арифметическое квадратов отклонений. Эту величину называют дисперсией (то есть разброс данных). Обозначим значения случайной величины x 1, x 2,..., xn, а математическое ожидание этих значений – буквой М.
Дисперсия – это среднее арифметическое квадратов разностей между значениями случайной величины и ее средним значением. В наших обозначениях:
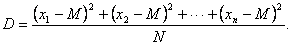
Или в общем виде дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее среднего значения.
Вероятностный смысл Дисперсия случайной величины Х есть характеристика рассеивания разбросанности значений случайной величины около ее математического ожидания. Дисперсия случайной величины имеет размерность квадрата случайной величины.
Метод сравнения средних значений и дисперсий используется в самых разных отраслях человеческой деятельности. В медицине – для установления диагноза, в литературоведении – для определения автора произведения (когда авторство является спорным), в криминалистике – для розыска преступников.
Вычисления громоздки, есть формула, позволяющая быстрее вычислить значение дисперсии.
Формула для вычисления дисперсии
D (X) = M (X)2 – [ M (X)]2
Пример.
| X | |||
| P | 0,1 | 0,6 | 0,3 |
M (X) = 2 . 0,1 + 3 . 0,6 + 5 . 0,3 = 0,3 + 1,0 + 1,0 = 3,5.
| X 2 | |||
| P | 0,1 | 0,6 | 0,3 |
M (X 2) = 4 . 0,1 + 9 . 0,6 + 25 . 0,3 = 0,3 + 1,0 + 1,0 = 13,3
D (X) = M (X)2 – [ M (X)]2 = 13,3 – (3,5)2 = 10,5
Свойства дисперсии
1. Дисперсия постоянной величины равна нулю D (C) = 0
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D (CX) = C 2 D (X)
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D (X + Y) = D (X) + D (Y)
4. Дисперсия разности двух независимых величин равна сумме их дисперсий D (X – Y) = D (X) + D (Y)
Следствия
5. D (C + X) = D (X) где С – const.
6. D (X + Y + Z) = D (X) + D (Y) + D (Z)
Пример. D (X) = 2 D (4 X + 5) = D (4 X) + D (5) = 16 D (X) + 0 = 16 . 2 = 32
Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых р – вероятность появления постоянна: D (X) = n . p . q.
Пример. Производится 10 независимых испытаний р = 0,6.
D (X) = n . p . q = 10 . 0,6 . 0,4 = 2,4