Содержание и порядок выполнения контрольной работы
Работа состоит из шести заданий связанных между собой одним общим условием выбором двух векторов: одного общего вектора для всех, вектора а = 2 e 1 + e 2 + e 3 и второго вектора b, первая компонента которого равна единице, а вторая и третья берутся по предпоследней и последней цифрам шифра соответственно. Так, например, если две последние цифры шифра студента 23, то вектор b = e 1 + 2 e 2 + 3 e 3.
1. Вычислить скалярное, векторное и неопределенное произведения векторов а и b, а также вычислить угол между этими векторами. Для проверки результатов расчет угла следует провести двумя способами. Через формулу скалярного произведения векторов а и b и через формулу модуля векторного произведения этих векторов.
2. Определить диадик D, как векторное произведение вектора с = а  b и диады ab.
b и диады ab.
3. Разложить диадик D на симметричную M и антисимметричную N части.
4. Вычислить вектор антисимметричного тензора.
5. Найти главные значения и направления главных осей тензора М. При этом кубическое уравнение контролируется значениями первого, второго и третьего инвариантов тензора М, а корни кубического уравнения так же проверяются через инварианты этого тензора.
Из полученных значений направляющих косинусов координатных осей составляется тензор преобразований А, который также необходимо проверить на удовлетворение условий ортогональности.
6. Матричным умножением тензоров второго ранга тензор М преобразовать к главным осям.
Все вычисления необходимо производить с большой точностью и результаты округлять до десятитысячных, цифры должны быть написаны четко и правильно.
Пример выполнения задания
Имеем два вектора представленных через свои компоненты в прямоугольной декартовой системе координат
а = 2 e 1 + e 2 + e 3, b = 2 e 1 + 2e2 + 3e3.
1. Вычисление произведений векторов.
Используя свойства единичных векторов, вычисляем скалярное и векторное произведения векторов а и b
а • b = (2 e 1 + e 2 + e 3) • (2 e 1 + 2 e 2 + 3 e 3)=4 e 1 • e 1 + 2 e 2 • e 2 + 3 e 3 • e 3 = 9, с = а  b = (2 e 1 + e 2 + e 3)
b = (2 e 1 + e 2 + e 3)  (2 e 1 + 2 e 2 + 3 e 3) = 4(e 1
(2 e 1 + 2 e 2 + 3 e 3) = 4(e 1  e 2) + 6( e 1
e 2) + 6( e 1  ё3) + 2(e 2
ё3) + 2(e 2  e 1) + 3(e 2
e 1) + 3(e 2  e 3) + 2(e 3
e 3) + 2(e 3  e 1) + 2(e 3 х e 2) = 4 e 3 - 6 e 2 - 2 e 3 + 3 e 1 + 2 e 2 - 2 e 1 = e e 1 - 4 e 2 + 2 e 3.
e 1) + 2(e 3 х e 2) = 4 e 3 - 6 e 2 - 2 e 3 + 3 e 1 + 2 e 2 - 2 e 1 = e e 1 - 4 e 2 + 2 e 3.
Модуль вектора с равен
| с | =  = 4,5826.
= 4,5826.
Векторное произведение проще вычислить через определитель
с = а  b =
b = 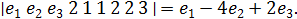
Из формулы скалярного произведения векторов определяется косинус угла между векторами
cos (а  b) =
b) = 
откуда а  b = 26,9841°.
b = 26,9841°.
Для проверки результата расчета вычислим этот угол с помощью формулы модуля векторного произведения векторов
sin (а  b) =
b) = 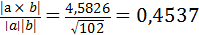
откуда а  b = 26,9841°.
b = 26,9841°.
Наконец вычисляем неопределенное произведение этих векторов ab = (2  1 +
1 +  2 +
2 +  3)(2
3)(2  1 + 2
1 + 2  2 + 3
2 + 3  3 ) =
3 ) =
= 4 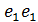 + 4
+ 4  1
1  2 + 6
2 + 6  1
1  3 + 2
3 + 2  2
2  1 + 2
1 + 2  2
2  2 + 3
2 + 3  2
2  3 + 2
3 + 2  3
3  1 + 2
1 + 2  3
3  2 + 3
2 + 3  3
3  3 Матрица этого тензора второго ранга имеет вид
3 Матрица этого тензора второго ранга имеет вид
 .
.
2. Вычисление диадика.
Вычисляем диадик D через векторное произведение вектора с и диады ab
D = с  ab = (
ab = ( - 4
- 4  2 + 2
2 + 2  3)
3)  (
( 1+ 4
1+ 4  1
1  2 + 6
2 + 6  1
1  3 + 2
3 + 2  2
2  1 + 2
1 + 2  2
2  2 + 3
2 + 3  2
2  3 + 2
3 + 2  3
3  1 + 2
1 + 2  3
3  2 + 3
2 + 3  3
3  3) = 2(
3) = 2(
 2)
2)  1 + 2(
1 + 2( 1
1  2)
2)  2 + 3(
2 + 3( 1
1  2)
2)  3 + 2(
3 + 2( 1
1  3)
3)  1 + 2(
1 + 2( 1 x
1 x  3)
3)  2 +
2 +
3( 1
1 
 3)
3)  3 -16(
3 -16( 2
2  )
)  1-16(
1-16(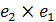 )
) 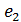 - 24(
- 24(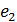
 1)
1)  3 - 8(
3 - 8( 2
2  3)
3)  1 - 8(
1 - 8( 2
2  3)
3)  2 "
2 "
12( 2
2 
 3)
3)  3 + 8(
3 + 8( 3
3  1)
1)  1 + 8(
1 + 8( 3
3  1)
1)  2 + 12(
2 + 12( 3
3  1)
1)  3 + 4(
3 + 4(  3
3  2)
2)  1 + 4(
1 + 4(  3
3  2)
2)  2 + 6(
2 + 6( 3
3  2)
2)  3 = – 12
3 = – 12  1
1  1 -12
1 -12  1
1  2 -18
2 -18  1
1  3 + 6
3 + 6  2
2  1 + 6
1 + 6  2
2  2 + 9
2 + 9  2
2  3 + 18
3 + 18  3
3  1 +18
1 +18  3
3  2 + 27
2 + 27 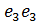 .
.
Это вычисление проще выполнить с помощью определителя
D = с  ab = ( с
ab = ( с  a ) b =
a ) b = 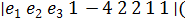 2
2  1 + 2
1 + 2  2 + 3
2 + 3  3) = -12
3) = -12  1
1  1 - 12
1 - 12  1
1  2 - 18
2 - 18  1
1  3 + 6
3 + 6  2
2  1 + 6
1 + 6  2
2  2 +
2 +
9  2
2  + 18
+ 18  3
3  1 +18
1 +18  3
3  2 + 27
2 + 27  3
3  3.
3.
Матрица диадика D имеет вид
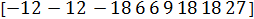 .
.
3. Разложение диадика.
Разлагается диадик D на симметричный М и антисимметричный N по формулам
D = M + N =  (D + Dc) +
(D + Dc) +  (D - D c),
(D - D c),
где Dc - сопряженный диадик, матрица которого имеет вид
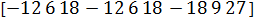
Разложение легче произвести матричным способом

И согласно полученных матриц записать симметричный М и антисимметричный тензор N в линейной форме
M = -12 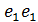 - 3
- 3  1
1  2 -3
2 -3  2
2  1 + 6
1 + 6  2
2  2 + 13,5
2 + 13,5  2
2  3 + 13,5
3 + 13,5  3
3  2 + 27
2 + 27  3
3  3.
3.
N = -9  1
1  2 - 18
2 - 18  1
1  3 + 9
3 + 9  2
2  1 - 4,5
1 - 4,5  2
2  3 + 18
3 + 18  3
3  1 + 4,5
1 + 4,5  3
3  2.
2.
4. Вычисление вектора диадика.
Вектор диадика N получается, если все диады ортов заменить их векторными произведениями
 = -9(
= -9(  1
1  2) -18
2) -18 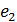
 3) + 9(
3) + 9( 2
2  1) - 4,5(
1) - 4,5( 2
2  3) + 18(
3) + 18( 3
3  1) + 4,5(
1) + 4,5( 3
3  2) =
2) =
= -9  3 +18
3 +18  2 - 9
2 - 9  3 - 4,5
3 - 4,5  1 +18
1 +18  2 - 4,5
2 - 4,5  1 = -9
1 = -9  1 + 36
1 + 36  2 -18
2 -18  3.
3.
5. Нахождение главных значений и направлений главных осей.
Для получения кубического уравнения составляем определитель и приравниваем его нулю
 = 0,
= 0,
где  - корни кубического уравнения.
- корни кубического уравнения.
Раскрыв определитель, получим кубическое уравнение вида
 3 – JI
3 – JI  + JII
+ JII  – JIII = 0.
– JIII = 0.
В нашем случае
 3 - 21
3 - 21  2 - 425,5
2 - 425,5  = 0, (1)
= 0, (1)
которое можно проверить, используя инварианты тензора M
JI = М11 + М22 + М33 = -12 + 6 + 27 = 21,
JII =  = - 81 - 20,25 - 324 = - 425,25,
= - 81 - 20,25 - 324 = - 425,25,
J iii = 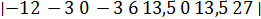 = -12(162 -182,25) - 243 = 0.
= -12(162 -182,25) - 243 = 0.
Решая уравнение (1), получаем три корня, которые располагаем в порядке убывания
 (1) = 33,6409,
(1) = 33,6409,  (2) = 0,
(2) = 0,  (3) = -12,6409.
(3) = -12,6409.
Они являются главными значениями симметричного тензора М.
Правильность вычисления корней уравнения (1) также можно проверить с помощью инвариантов
J I =  (1) +
(1) +  (2) +
(2) +  (3) = 33,6409 -12,6409 = 21,
(3) = 33,6409 -12,6409 = 21,
JII =  (1)
(1)  (2) +
(2) +  (2)
(2)  (3) +
(3) +  (3)
(3)  (1) = (-12,6409)(33,6409) = -425,25,
(1) = (-12,6409)(33,6409) = -425,25,
J III =  (1)
(1)  (2)
(2)  (3) = 0.
(3) = 0.
Используя значения корней, составляем систему трех линейных однородных уравнений для определения направляющих косинусов n1, n2, n3 для каждого главного направления.
При  (1) = 33,6409 система имеет вид
(1) = 33,6409 система имеет вид
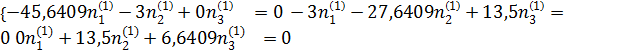 (2)
(2)
Так как определитель системы (2) равен нулю, то система имеет бесчисленное множество решений, выраженных через параметр t. При отыскании параметра t будем требовать, чтобы выполнялось условие nini = t.
Для определения значений 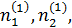
 воспользуемся двумя последними уравнениями системы (2)
воспользуемся двумя последними уравнениями системы (2)
n1(1) = 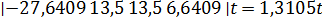 ,
,
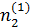 =
= 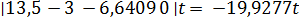 ,
,
n3(1) =  – 40,5t,
– 40,5t,
где t = 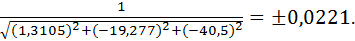
Подставляя значения t в систему (3), получим значения направляющих
косинусов для первого главного направления
n1(1) = ±0,0290, 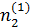 =
= 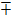 0,4413, n3(1) =
0,4413, n3(1) =  0,8969.
0,8969.
Аналогично определяем направляющие косинусы для второго и третьего главных направлений
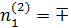 0,2182,
0,2182, 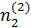 = ±0,8729,
= ±0,8729, 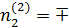 0,4364,
0,4364,

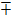 0,9755,
0,9755, 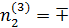 0,2084,
0,2084, 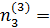 ±0,0709.
±0,0709.
Тензор преобразования А для данного случая будет иметь следующий вид
А = 
При правильно выполненных расчетах тензор А соответствует условию ортогональности. Сумма квадратов компонентов любого столбца или строки должна быть равна единице, сумма произведений компонент одинакового индекса двух столбцов или строк должна быть равна нулю.
6. Вычисление тензора М в главных осях.
Для приведения тензора М к главным осям воспользуемся формулой
M • = A · M · Ac,
где М• - тензор М в главных осях 
Ас - тензор, сопряженный с А.

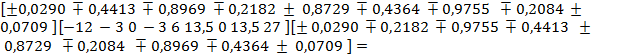
=  .
.
 =
= 
Варианты заданий по теоретическому материалу для студентов заочного обучения (необходимо дать определение и записать расчётные формулы):
Вариант 1.
1. Основные гипотезы механики сплошной среды.
2. Способ Лагранжа и Эйлера описания движения СС.
3. Переход от переменных Лагранжа к переменным Эйлера и наоборот
4. Понятие поля. Скалярное, векторное и тензорное поля.
Вариант 2.
1. Нормальные и касательные напряжения. Закон Паскаля.
2. Полная, частная и конвективная производные
3. Линия тока, поверхность тока, трубка тока. Дифференциальное уравнение линий тока в проекциях
4. Что такое вектор - градиент скалярной функции в точке?
Вариант 3.
1. Как определяется поток скорости через замкнутую поверхность? Что такое расхождение или дивергенция скорости?
2. Формула Гаусса.
3. Циркуляция скорости, ротор и вихрь.
4. Необходимое и достаточное условие существования потенциальных течений.
Вариант 4.
1. Закон сохранения массы.
2.Уравнение неразрывности для несжимаемой жидкости и стационарных течений.
3.Средние характеристики среды, где они применяются?
4.Обобщение уравнения неразрывности для многокомпонентых смесей.
Вариант 5.
1. Понятие деформации. Симметричный тензор деформаций. Соотношения Коши для малых деформаций.
2. Главные оси деформаций и главные удлинения.
3. Интенсивность деформаций. Главный сдвиг.
4. Характеристика деформационного состояния. Параметр Надаи.
Вариант 6.
1. Условия совместимости деформаций Сен – Венана.
2. Натуральные удлинения (укорочения).
3. Массовые и объёмные силы.
4. Нормальные и касательные напряжения.
Вариант 7.
1. Тензор напряжений. Характеристика напряжённого состояния в точке.
2. Главные напряжения. Средние напряжения. Диаграмма Мора.
3. Девиатор напряжений.
4. Интенсивность касательных напряжений.
Вариант 8.
1. Напряжения и деформации в твёрдых средах с точки зрения геодинамики
2. Литостатическое напряжение или давление
3. Принцип изостазии.
4. Задачи геодинамики, решаемые с помощью аппарата МСС.
Вариант 9.
1. Упругие и пластические деформации. Связь между напряжениями и деформациями в линейной теории упругости.
2. Параметры Ламе. Модуль Юнга. Коэффициент Пуассона.
3. Одноосное напряжённое состояние. Гуковское тело.
4. Одноосная деформация. Плоское напряжённое состояние. Плоская деформация.
Вариант 10.
1. Общие теоремы движения системы материальных точек.
2. Теорема живых сил. Уравнение баланса механической энергии.
3. Переход от интегральной формы уравнения движения к дифференциальной.
4. Математическая модель. Механические уравнения состояния.