Практика 12. Линии второго порядка
Знать: определение линии второго порядка на плоскости, окружности, эллипса, гиперболы, параболы; уравнения линий 2-го порядка, их свойства и алгоритмы построения.
Уметь: выводить уравнения линий 2-го порядка и строить их по данным уравнениям; находить уравнения касательных, асимптот и директрис этих линий.
Проверочная работа по теме: «Аналитическая геометрия на плоскости»
| Даны вершины треугольника А(2;-2), В(3;5), С(6;1). Найти: | ||
| 1 вар. | 1. Общее уравнение прямой, на которой лежит высота, проведенная из точки В. | 2. Длину медианы АМ. |
| 2 вар. | 1. Общее уравнение прямой, на которой лежит медиана, проведенная из точки А. | 2. Длину высоты ВК. |
Решение проверочной работы:
| 1 вариант | |
1. 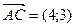 4(x-3)+3(y-5)=0
4x+3y-27=0
Ответ: 4х+3у-27=0
4(x-3)+3(y-5)=0
4x+3y-27=0
Ответ: 4х+3у-27=0
| 2. M(4,5;3)
AM= 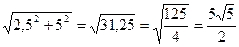 Ответ: АМ=
Ответ: АМ= 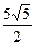
|
| 2 вариант | |
1. М(4,5; 3)
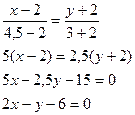 Ответ: 2х-у-6=0
Ответ: 2х-у-6=0
| 2. АС: 
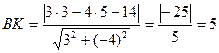 Ответ: 5
Ответ: 5
|
Работа в аудитории:
1.3. Найти координаты центра и радиус окружности  . .
| 1.4. Написать уравнение окружности, проходящей через точки (-1;3), (0;2), (1;-1). | 1.5. Написать уравнения касательных к окружности  , проведенных из точки М(0;3). , проведенных из точки М(0;3).
|
2.3. Найти оси, центр и эксцентриситет эллипса, заданного уравнением  . Построить этот эллипс. . Построить этот эллипс.
| 2.4. Составить уравнение эллипса, проходящего через точки 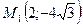 и и  . .
| 2.5. Найти уравнение касательной к эллипсу  , перпендикулярной прямой , перпендикулярной прямой  . .
|
3.3. Дано уравнение гиперболы 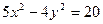 . Найти длины ее полуосей, координаты фокусов, эксцентриситет и уравнения асимптот гиперболы. . Найти длины ее полуосей, координаты фокусов, эксцентриситет и уравнения асимптот гиперболы.
| 3.4. Найти уравнение гиперболы, фокусы которой находятся в точках  и и  , а длина мнимой оси равна 6. Построить эту гиперболу. , а длина мнимой оси равна 6. Построить эту гиперболу.
| 3.5. Найти угол между асимптотами гиперболы, если ее эксцентриситет равен 2. |
4.3. Дана парабола  . Найти координаты ее фокуса и уравнение директрисы. . Найти координаты ее фокуса и уравнение директрисы.
| 4.4. Найти вершину, фокус и директрису параболы 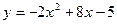 , построить эскиз графика. , построить эскиз графика.
| 4.5. При каких значениях  прямая прямая  касается параболы касается параболы 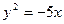 . .
|
| 5. Установить тип кривой и сделать эскиз линии: | ||
5.3.  . .
| 5.4.  . .
| 5.5.  . .
|
Решения:
1.3. Найти координаты центра и радиус окружности  .
.
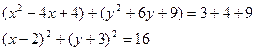
Ответ: С(2; -3), R=4.
1.4. Написать уравнение окружности, проходящей через точки (-1;3), (0;2), (1;-1).
Пусть (х0, у0) – координаты центра окружности, а r – ее радиус, тогда


Ответ: (-4; -1), r=5.
1.5. Написать уравнения касательных к окружности  , проведенных из точки М(0;3).
, проведенных из точки М(0;3).
Пусть касательные имеют уравнения в виде 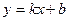 . Т.к. она проходит через М(0;3), то
. Т.к. она проходит через М(0;3), то  .
.
Уравнение окружности запишем в виде  .
.
Тогда система уравнений 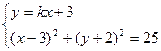 имеет одно решение.
имеет одно решение.
Или уравнение  имеет один корень.
имеет один корень.

Квадратное уравнение имеет один корень, если D=0.

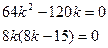
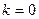 или
или  .
.
Ответ:  или
или 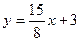 .
.
2.3. Найти оси, центр и эксцентриситет эллипса, заданного уравнением  . Построить этот эллипс.
. Построить этот эллипс.


Это уравнение эллипса с центром в точке (1; -2), осями  и
и 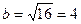 , эксцентриситетом
, эксцентриситетом 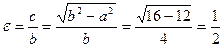 , т.к.
, т.к.  .
.
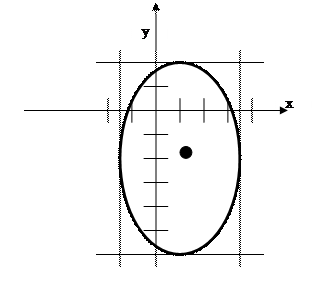
Ответ: центр (1; -2), оси  и
и  , эксцентриситет
, эксцентриситет  .
.
2.4. Составить уравнение эллипса, проходящего через точки 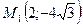 и
и  .
.
Пусть уравнение эллипса имеет вид  .
.
Т.к. эллипс проходит через точку 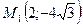 , то
, то  .
.
Т.к. эллипс проходит через точку  , то
, то 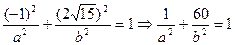 .
.
Составим и решим систему 




Ответ: 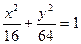 .
.
2.5. Найти уравнение касательной к эллипсу  , перпендикулярной прямой
, перпендикулярной прямой  .
.
Пусть уравнение касательной прямой имеет вид  , т.к. искомая прямая перпендикулярна прямой
, т.к. искомая прямая перпендикулярна прямой  , то имеет вид
, то имеет вид  .
.
Т.к. прямая  и эллипс
и эллипс  касаются, то система
касаются, то система  имеет одно решение. Или т.к.
имеет одно решение. Или т.к.  , то уравнение
, то уравнение  имеет один корень.
имеет один корень.

Квадратное уравнение имеет один корень, если 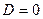 .
.


Ответ: 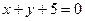 или
или 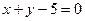 .
.
3.3. Дано уравнение гиперболы 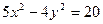 . Найти длины ее полуосей, координаты фокусов, эксцентриситет и уравнения асимптот гиперболы.
. Найти длины ее полуосей, координаты фокусов, эксцентриситет и уравнения асимптот гиперболы.
Приведем данное уравнение к каноническому  .
.
Тогда ее полуоси равны  и
и  .
.
Найдем 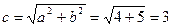 . Значит, фокусы имеют координаты
. Значит, фокусы имеют координаты  и
и  .
.
Вычислим эксцентриситет  .
.
Найдем уравнения асимптот 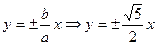 .
.
Ответ: полуоси  и
и  , фокусы
, фокусы  и
и  , эксцентриситет
, эксцентриситет  , уравнения асимптот
, уравнения асимптот  .
.
3.4. Найти уравнение гиперболы, фокусы которой находятся в точках  и
и  , а длина мнимой оси равна 6. Построить эту гиперболу.
, а длина мнимой оси равна 6. Построить эту гиперболу.
Т.к. фокусы  и
и  лежат на прямой
лежат на прямой 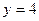 , то гипербола имеет вид
, то гипербола имеет вид  .
.
Длина мнимой оси гиперболы равна 6, значит, 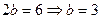 .
.
Расстояние между  и
и  равно
равно  .
.
Вычислим  .
.
Центр гиперболы является серединой отрезка  . Значит,
. Значит, 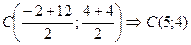 .
.
Таким образом, уравнение искомой гиперболы 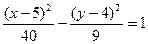 .
.

Ответ: 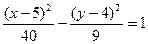 .
.
3.5. Найти угол между асимптотами гиперболы, если ее эксцентриситет равен 2.
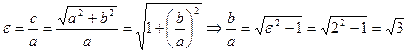 .
.
Тогда асимптоты имеют уравнения  .
.
Найдем угол между этими прямыми 
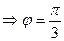 .
.
Ответ: 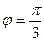 .
.
4.3. Дана парабола  . Найти координаты ее фокуса и уравнение директрисы.
. Найти координаты ее фокуса и уравнение директрисы.
Сравнивая данное уравнение параболы с каноническим уравнением вида 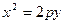 , заключаем, что
, заключаем, что  - фокус параболы, а
- фокус параболы, а 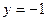 - уравнение директрисы.
- уравнение директрисы.
Ответ: 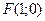 - фокус параболы,
- фокус параболы, 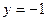 - уравнение директрисы.
- уравнение директрисы.
4.4. Найти вершину, фокус и директрису параболы 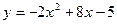 , построить эскиз графика.
, построить эскиз графика.
Преобразуем данное уравнение параболы к каноническому:

Значит, вершина имеет координаты (2;3). Т.к. 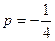 и прямая
и прямая 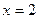 является осью симметрии, то фокус имеет координаты
является осью симметрии, то фокус имеет координаты  , а директриса имеет уравнение
, а директриса имеет уравнение  .
.

Ответ: (2;3) – вершина параболы,  - ее фокус,
- ее фокус, 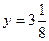 - уравнение директрисы.
- уравнение директрисы.
4.5. При каких значениях  прямая
прямая  касается параболы
касается параболы 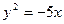 .
.
Прямая  касается параболы
касается параболы 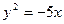 , если система
, если система  имеет единственное решение или уравнение
имеет единственное решение или уравнение 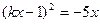 имеет один корень.
имеет один корень.

Квадратное уравнение имеет один корень, если его 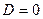 .
.

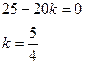
Ответ: при 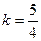 .
.
5.3.  .
.
Преобразуем данное уравнение:

Эта система задает часть параболы, находящуюся под прямой  . Парабола имеет вершину (1;3) и ее ветви направлены вправо.
. Парабола имеет вершину (1;3) и ее ветви направлены вправо.

5.4.  .
.

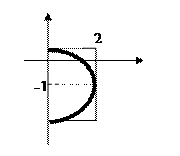
Эта система задает часть эллипса, находящегося правее прямой  . Эллипс имеет центр (0;-1) и полуоси
. Эллипс имеет центр (0;-1) и полуоси  и
и  .
.
5.5. 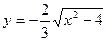 .
.

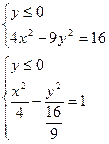
Эта система задает часть гиперболы, расположенную под прямой 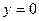 . Гипербола имеет центр (0;0) и полуоси
. Гипербола имеет центр (0;0) и полуоси  и
и 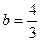 .
.
