КОНТРОЛЬНЫЕ ЗАДАНИЯ
для зачета по лабораторным работам
по дисциплине «Физика»
для студентов всех направлений и специальностей
очной формы обучения
Воронеж 2015
Составители: канд. физ.-мат. наук Е.П. Татьянина, канд. физ.-мат. наук А.Г. Москаленко, канд. физ.-мат. наук Т.Л. Тураева, канд. физ.-мат. наук Н.В. Матовых, канд. техн. наук М.Н. Гаршина
УДК 531 (07)
Электростатика. Постоянный ток. Электромагнетизм: контрольные задания для зачета по лабораторным работам по дисциплине «Физика» для студентов всех направлений и специальностей очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Е.П. Татьянина, А.Г. Москаленко, Т.Л. Тураева, Н.В. Матовых, М.Н. Гаршина. Воронеж, 2015. 38 с.
Методические указания содержат теоретический минимум и варианты контрольных заданий по дисциплине «Физика» для сдачи зачета по лабораторным работам «Электростатика. Постоянный ток. Электромагнетизм».
Предназначены для студентов первого курса очной формы обучения.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Контрольные задания_физика2.doc.
Ил. 74. Библиогр.: 5 назв.
Ответственный за выпуск зав. кафедрой канд. физ.-мат. наук, проф. Т.Л.Тураева
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВПО «Воронежский
государственный технический университет», 2015
Электростатика
Контрольные задания к лабораторной работе №2.1. Моделирование электростатических полей
Теоретический минимум
· Электрический заряд. Закон сохранения заряда. Закон Кулона.
· Электрическое поле. Напряженность электрического поля. Принцип суперпозиции и его применение к расчету напряженности полей.
· Поток вектора напряженности. Теорема Гаусса для электростатического поля в вакууме. Применение теоремы Гаусса к расчету полей.
· Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора напряженности. Потенциал.
· Силовые линии и эквипотенциальные поверхности. Графическое изображение полей. Связь между напряженностью и потенциалом.
Вариант №1
1. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции и его применение к расчету напряженности полей.
2. Точечные положительные заряды q и 2 q закреплены на расстоянии L друг от друга в вакууме (рис. а). Как изменятся модуль и направление силы, действующей на положительный заряд q, если на середине прямой, соединяющей заряды, поместить точечный отрицательный заряд – q (рис. б)?
3. Внутри полой тонкостенной сферы радиусом 2 R находится сфера радиусом R. Их центры совпадают. Сферы соответственно заряжены зарядами +2 q и + q. Чему равна напряженность электрического поля на расстоянии 3 R /2 от общего центра сфер?
4. Чему равен поток вектора напряженности электрического поля через поверхность сферы, в центре которой находится диполь с моментом 
?
5. Электростатическое поле создается положительным точечным зарядом. На расстоянии 10 см от заряда потенциал поля равен j = 100 В. Чему равно числовое значение градиента потенциала электрического поля в этой точке?
Вариант №2
1. Поток вектора напряженности. Теорема Гаусса для электростатического поля в вакууме.
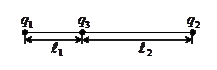2. Два заряда q 1 и q 2 закреплены на некотором расстоянии друг от друга. Третий заряд может перемещаться только вдоль прямой, проходящей через заряды. При каком отношении расстояний от этого заряда до зарядов q 1 и q 2 (
/ 
) он будет находиться в состоянии равновесия?
3. На каком графике показана зависимость напряженности электрического поля объемно заряженного шара радиуса R от расстояния r от центра шара?
4. В центре воображаемой сферы находится точечный заряд. Изменится ли поток вектора 
сквозь эту поверхность, если: а) добавить заряд за пределами сферы; б) изменить радиус сферы?
5. Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью s = 5 нКл/м2 (
). Чему равно числовое значение градиента потенциала этого поля и как он направлен?
Вариант №3
1. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора напряженности. Потенциал.
2. Во сколько раз уменьшится сила кулоновского отталкивания двух маленьких бусинок с одинаковыми зарядами, если, не меняя расстояния между ними перенести 2/3 заряда с первой бусинки на вторую?
3. На рисунке показано расположение двух неподвижных точечных зарядов +2 q и – q. В какой из трех точек - А, B или С – модуль вектора напряженности электрического поля этих зарядов минимален?
4. Вблизи равномерно заряженной нити построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью. Как изменится модуль потока вектора через полную поверхность цилиндра, если нить наклонить?
5. Рассчитайте электрический потенциал поверхности Земли, если радиус планеты 6400 км, а напряженность на поверхности Земли 130 В/м.
Вариант №4
1. Силовые линии и эквипотенциальные поверхности. Графическое изображение полей. Связь между напряженностью и потенциалом.
2. Два одинаковых металлических шарика, заряженных одноименными зарядами q и 4 q, находятся на расстоянии r друг от друга. Шарики привели в соприкосновение. На какое расстояние их надо развести, чтобы сила взаимодействия осталась прежней?
3. На рисунке изображен вектор напряженности электрического поля в точке С. Поле создано двумя точечными зарядами 
и 
. Чему равен заряд , если заряд = +1 мкКл?
4. Определить напряженность электрического поля, создаваемую бесконечной тонкой плоской поверхностью, равномерно заряженной с поверхностной плотностью заряда σ.
5. В трех вершинах квадрата со стороной а находятся точечные заряды + q, +2 q и - q. Определите результирующий потенциал электрического поля в четвертой вершине.
Вариант №5
1. Используя теорему Гаусса, определите напряженность электрического поля внутри и вне равномерно заряженной сферы, если полный заряд сферы q.
2. Два маленьких одинаковых металлических шарика заряжены положительным зарядом 5 q и отрицательным зарядом – q и находятся на некотором расстоянии друг от друга в вакууме. Шарики привели в соприкосновение и развели на прежнее расстояние, поместив их в жидкий диэлектрик с e = 2. Как при этом изменился модуль силы взаимодействия?
3. Точки А, B, C и D расположены на прямой и разделены равными промежутками (см. рис.). В точке А помещен заряд 
, в точке В 
. Какой заряд 
надо поместить в точку D, чтобы напряженность поля в точке С была равна нулю?
4. Дана система точечных зарядов в вакууме и замкнутые поверхности S 1, S 2 и S 3 (см. рис.). Найдите поток вектора напряженности электростатического поля через указанные поверхности.
5. Проводящий шар радиусом 5 см заряжен до потенциала 40 В. Определите значение напряженности поля на расстоянии 3 см от поверхности шара.
Вариант №6
1. Используя теорему Гаусса, определите напряженность электрического равномерно заряженной бесконечной нити, если линейная плотность заряда 
.
2. В вершинах равностороннего треугольника со стороной a, находятся точечные заряды + q, - q, +2 q как показано на рисунке. Определите результирующую силу, девствующую на заряд + q со стороны двух других.
3. На каком графике показана зависимость напряженности поля равномерно заряженного бесконечного пустотелого цилиндра радиуса R от расстояния r от оси цилиндра?
4. Определитепоток вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды Q 1=5 нКл и Q 2=-2 нКл ().
5. В некоторой области пространства создано электростатическое поле, потенциал которого определяется функцией 
. Какое направление имеет вектор напряженности электрического поля в точке пространства, показанной на рисунке?
Вариант №7
1. Используя теорему Гаусса, определите напряженность электрического поля равномерно заряженной бесконечной плоскости, если поверхностная плотность заряда плоскости 
.
2. Как направлена кулоновская сила, действующая на отрицательный точечный заряд, помещенный в центре квадрата, в вершинах которого находятся заряды + q, + q, - q, - q (см.рис.)?
3. Точка В находится в середине отрезка AC. Неподвижные заряды - q и -2 q расположены в очках A и C соответственно (см.рис.). Какой заряд надо поместить в точку С взамен заряда -2 q, чтобы напряженность электрического поля в точке В увеличилась в 2 раза.
4. Плоская квадратная пластина со стороной а = 20 см находится на некотором расстоянии от бесконечной равномерно заряженной (s =0,5 мкКл/м2) плоскости. Плоскость пластины составляет угол a =60о с линиями поля. Определите поток напряженности электрического поля через эту пластину ().
5. Является ли эквипотенциальной плоскость симметрии 
в поле точечных зарядов: а) q1=q2=q; б) q1=+q; q2=-q?
Контрольные задания к лабораторным работам: №2.2. Определение ёмкости конденсаторов посредством измерения тока разрядки; №2.3. Определение электроемкости конденсаторов мостиком Соти
Теоретический минимум
· Электроемкость уединенного проводника и конденсатора.
· Расчет емкости плоского, сферического и цилиндрического конденсаторов.
· Соединение конденсаторов.
· Энергия электрического поля точечных зарядов и конденсаторов. Объемная плотность энергии электрического поля.
· Проводники и диэлектрики в электрическом поле.
Вариант 1
1. Электроемкость уединенного проводника и конденсатора.
2.Какого радиуса должен быть проводящий шар, чтобы его электроемкость в вакууме равнялась С =1 Ф?
3. К конденсатору, электроемкость которого C =16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй последовательно (см.рис.). Емкость образовавшейся батареи конденсаторов равна С. Какова емкость Х?
4. Присоединенный к источнику тока конденсатор, заполненный диэлектриком с диэлектрической проницаемостью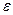 
, имеет энергию W. Если удалить диэлектрик, то чему станет равна энергия электрического поля конденсатора?
5. На рисунке дано графическое изображение электрического поля. Данному рисунку соответствует подпись:
1) линии напряженности, e1>e2
2) линии напряженности, e1<e2
3) линии электрического смещения, e1>e2
4) линии электрического смещения, e1<e2
Вариант 2
1. Соединение конденсаторов.
2. Найти емкость сферического конденсатора, радиусы обкладок которого равны 
и 
( > ), если пространство между обкладками заполнено однородным диэлектриком с проницаемостью .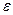
3. Рассчитайте э лектрическую емкость плоского конденсатора площадью пластин S с двумя слоями диэлектриков толщиной d 1 и d 2 и диэлектрической проницаемостью e1 и e2.
4. Разность потенциалов между точками А и В составляет 1000 В. Энергия батареи конденсаторов равна 2 Дж. Вычислите емкость каждого конденсатора.
5. Два точечных заряда с зарядами +12 нКл и –12 нКл, образуя диполь, находятся на расстоянии 0,3 см. Какую работу необходимо совершить, чтобы повернуть диполь на 900 в электрическом поле напряженности 10 В/м, если изначально диполь был ориентирован по полю.
Вариант 3
1. Энергия электрического поля точечных зарядов и конденсаторов. Объемная плотность энергии электрического поля.
2. Найти емкость цилиндрического конденсатора, радиусы обкладок которого равны и ( > ), если пространство между обкладками заполнено однородным диэлектриком с проницаемостью .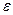
3. Два плоских конденсатора одинаковой электроемкости соединены в батарею последовательно и подключены к источнику тока. Затем пространство между пластинами второго конденсатора, не отключая источника тока, заполняют диэлектриком с диэлектрической проницаемостью e =3. Как и во сколько раз изменится разность потенциалов на пластинах первого конденсатора?
4. Напряженность электрического поля плоского воздушного конденсатора емкостью 4 мкФ равна 1000 В/м. Расстояние между обкладками 1 мм. Определите энергию электрического поля конденсатора.
5. На рисунке дано графическое изображение электрического поля. Данному рисунку соответствует подпись:
1) линии напряженности, e1>e2
2) линии напряженности, e1<e2
3) линии электрического смещения, e1>e2
4) линии электрического смещения, e1<e2
Вариант 4
1. Проводники в электрическом поле. Поле внутри и у поверхности проводника. Распределение зарядов внутри проводника. Электростатическая защита.
2. Определить электроемкость С плоского слюдяного конденсатора, площадь S пластин которого равна 100 см2, а расстояние между ними равно 0,1 мм.
3. Какой должна быть емкость конденсатора, который надо соединить последовательно с конденсатором емкостью 800 пФ, чтобы получить батарею конденсаторов емкостью 160 пФ?
4. Пластины изолированного плоского конденсатора емкостью С и с зарядом q раздвигают так, что расстояние между ними увеличивается в n раз. Рассчитайте, какую для этого нужно произвести работу.
5. В однородное электростатическое поле напряженностью Е0 =700 В/м перпендикулярно полю помещается бесконечная плоскопараллельная стеклянная (e =7) пластина. Чему равно электрическое смещение внутри пластины?
Вариант 5
1. Электрическое поле в диэлектрике. Поляризация диэлектрика. Поляризованность.
2. Напряженность поля в плоском воздушном конденсаторе с площадью пластин S равна Е. Определите поверхностную плотность заряда на пластинах конденсатора.
3.Конденсаторы емкостями 10 мкФ и 1,5 мкФ соединены параллельно. Суммарный заряд конденсаторов 2,3 мкКл. Определите заряд конденсатора большей емкости.
4. Расстояние между обкладками плоского воздушного конденсатора 0,3 см. Во сколько раз увеличится энергия электрического поля конденсатора, если обкладки конденсатора раздвинуть до расстояния 1,2 см? Конденсатор после сообщения ему электрического заряда был отключен от источника напряжения.
5. Расстояние между пластинами плоского конденсатора равно 2 мм, разность потенциалов 1,8 кВ. Диэлектрик – стекло (e =7). Определите диэлектрическую восприимчивость стекла и поверхностную плотность связанных зарядов на поверхности стекла.
Вариант 6
1. Электрическое смещение. Диэлектрическая проницаемость. Теорема Гаусса для диэлектриков.
2. Определить емкость плоского конденсатора, если известна площадь пластин S и расстояние между ними d.
3. Три конденсатора соединены, как показано на рисунке. Какой заряд накоплен всеми конденсаторами? Напряжение подведенное к точкам А и В, равно 250 В. Электроемкости С 1=1,5 мкФ, С 2=3,0 мкФ, С 3=4,0 мкФ.
4. Плоский воздушный конденсатор подключили к источнику напряжения и затем отключили от него. После этого сдвинули пластины конденсатора, уменьшив зазор в два раза. Как изменилась при этом объемная плотность энергии электрического поля в конденсаторе?
5. Пространство между пластинами заполнено парафином (ε =2). Расстояние между пластинами d =8,85 мм. Какую разность потенциалов необходимо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,1 нКл/см2?
Вариант 7
1. Граничные условия на поверхности раздела двух диэлектриков.
2.Определить электроемкость уединенного проводящего шарика диаметром 3 см в воздухе.
3. Два конденсатора, емкости которых 2 мкФ и 4 мкФ, соединены последовательно и подключены к источнику напряжения с ЭДС 75 В. Найдите разность потенциалов на конденсаторе большей емкости.
4. Конденсатор заполняют трансформаторным маслом. Как изменится его энергия, если а) конденсатор подключен к источнику; б) конденсатор заряжен и отключен от источника?
5. В однородное электростатическое поле напряженностью Е 0 = 700 В/м перпендикулярно полю помещается бесконечная плоскопараллельная стеклянная (e =7) пластина. Чему равна поляризованность стекла?
Постоянный ток
2.1. Контрольные задания к лабораторным работам:
№2.4. Определение ЭДС источника методом компенсации;
№2.5. Измерение сопротивления проводников мостиком Уитстона; №2.6. Изучение обобщенного закона Ома
Теоретический минимум
· Сила и плотность тока. Связь между вектором плотности тока и скоростью упорядоченного движения зарядов.
· Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах.
· Сторонние силы, ЭДС и напряжение.
· Обобщенный закон Ома.
· Правила Кирхгофа и их применение к расчету разветвленных цепей.
· Классическая теория электропроводности металлов. Вывод законов Ома и Джоуля-Ленца на основе электронной теории.
Вариант 1
1. Дайте понятие силы и плотности тока. Какова связь плотности тока со скоростью упорядоченного движения зарядов?
2. Количество электричества, проходящее через поперечное сечение проводника, изменяется со временем по закону q=9+8t–t2. Через какое время ток поменяет свое направление на противоположное?
3. Амперметр с сопротивлением RA = 0,16 Ом зашунтирован сопротивлением R = 0,04 Ом. Чему равен ток в цепи, если амперметр показывает ток I0 = 8 А?
4. При прохождении через проводник электрического тока за время t выделилось количество теплоты, равное Q. Объем проводника V, удельное сопротивление r. Чему равна напряженность электрического поля в проводнике?
5. В представленной схеме ЭДС первого и второго источников равны E1= E2 =2В, ЭДС третьего E 3= 5В, сопротивления R1=1 Ом, R2=R3=2Ом. Какова разность потенциалов между точками А и В?
Вариант 2
1. Сформулируйте закон Ома в интегральной и дифференциальной форме для однородного и неоднородного участка цепи.
2. Ток в проводнике меняется со временем по уравнению I = 4 + 2t (А). Какое количество электричества, пройдет через поперечное сечение проводника за время 5с?
3. ЭДС батареи аккумуляторов E =12 В. Если сила тока в цепи равна I = 4 А, а напряжение на клеммах батареи U = 11 В, то чему будет равен ток короткого замыкания?
4. Чему равно показание амперметра, если E=6В, R1=4Ом, R2=6Ом, RV =12 Ом?
5. Чему равна удельная тепловая мощность в медном проводе при плотности электрического тока 10 А/см2? Удельное сопротивление меди 17 нОм∙м.
Вариант 3
1. Какую роль выполняют сторонние силы в источнике тока? Электродвижущая сила и ее связь с напряженностью поля сторонних сил.
2. Ток в проводнике меняется со временем по уравнению I=4+2t (А). Какое количество электричества пройдет через поперечное сечение проводника за время от t1=2с до t2=6с?
3. Определите показания амперметра в данной цепи. Параметры цепи: E=6В, R1=4Ом, R2=6Ом, RV=12 Ом.
4. По проводу сечением S и удельным сопротивлением r течет ток I. Получите выражение для силы, действующей на отдельные свободные электроны со стороны электрического поля.
5. На каком из резисторов при прохождении постоянного тока выделится максимальное количество теплоты?
Вариант 4
1. Как определяется работа и мощность тока? Сформулируйте закон Джоуля-Ленца в интегральной и дифференциальной форме.
2. Неоднородный участок цепи это –
1) участок, на котором действуют только электрические силы;
2) участок, на котором действуют электрические и сторонние силы;
3) участок, на котором действуют только сторонние силы;
4) участок с неоднородным удельным сопротивлением.
3. Как изменится ток короткого замыкания, если два одинаковых источника тока пересоединить из параллельного соединения в последовательное?
4. Напряженность электрического поля в проводнике равна Е. Объем проводника V, удельное сопротивление r. Какое количество теплоты выделится при прохождении через проводник электрического тока за время t?
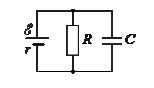5. Определите заряд на обкладках конденсатора в электрической цепи, представленной на рисунке.
Вариант 5
1. Сформулируйте правила Кирхгофа для разветвленных цепей. Как определяются в уравнениях Кирхгофа знаки для ЭДС, токов и падений напряжений?
2. По проводнику сечением S течет ток I. Плотность и молярная масса материала проводника соответственно равны r и М. На каждый атом материала приходится один свободный электрон. Получите выражение для средней скорости упорядоченного движения электронов вдоль проводника.
3. Какое количество теплоты выделится за единицу времени в единице объема медного провода (r = 17 нОм∙м), при плотности тока j = 300 кА/м2?
4. Два параллельно соединенных элемента с одинаковыми ЭДС E1= E2=2В и внутренними сопротивлениями r1=1Ом, r2 = 1,5 Ом замкнуты на внешнее сопротивление R=1,4Ом. Определите ток, протекающий во внешней цепи.
5. Две электрические лампочки сопротивлением 100 Ом и 300 Ом включены в сеть последовательно. Как различаются мощности, потребляемые лампочками?
Вариант 6
1. От чего зависит сопротивление проводников? Каков физический смысл удельного сопротивления и удельной проводимости? Последовательное и параллельное соединение проводников.
2. Рассчитайте среднюю скорость упорядоченного движения электронов в проводнике с концентрацией n =1029 м-3 при плотности тока j =100 А/см2.
3. Определить сопротивление участка цепи АВ
4. При какой плотности тока в медном проводе (
) удельная тепловая мощность тока будет равна 720 Дж/м3∙с?
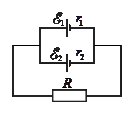5. Два параллельно соединенных элемента с одинаковыми ЭДС E 1= E2 =2В и внутренними сопротивлениями r1=1Ом, r2 = 1,5 Ом замкнуты на внешнее сопротивление R = 1,4 Ом. Чему равен ток, протекающий через второй элемент?
Вариант 7
1. Что представляет собой неоднородный участок цепи? Сформулируйте закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме.
2. Ток в проводнике меняется со временем по уравнению I=18 - 6t (А). Какое количество электричества, пройдет через поперечное сечение проводника за 6 секунд?
3. Что покажет вольтметр при следующих параметрах схемы: E=6 В, R1 = 4 Ом, R2=6 Ом, RV=12 Ом?
4. Каков КПД цепи, если E =2В, r = 0,4 Ом, I = 1 А?
5. Лампочки мощностью W1 = 100 Вт и W2 = 200 Вт соединены последовательно и включены в цепь постоянного тока. Как будут относиться мощности, потребляемые лампочками в этом случае?
Магнетизм
Контрольные задания к лабораторным работам:
№2.8а, 2.8б. Определение удельного заряда электрона с помощь магнетрона
Теоретический минимум
· Магнитное поле. Индукция магнитного поля. Поле движущегося заряда.
· Закон Био-Савара-Лапласа. Принцип суперпозиции. Поле прямого и кругового токов.
· Теорема Гаусса и теорема о циркуляции вектора магнитной индукции. Применение теоремы о циркуляции для расчета поля соленоида и тороида.
· Сила Ампера. Взаимодействие параллельных токов. Контур с током в магнитном поле. Работа по перемещению проводника и контура с током в магнитном поле.
· Сила Лоренца. Движение заряженных частиц в магнитном поле.
Вариант 1
1 Закон Био-Савара-Лапласа. Принцип суперпозиции для индукции магнитного поля. Поле прямого и кругового токов.
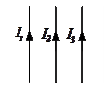2. Три бесконечно длинных параллельных проводника с токами расположены на равных расстояниях один от другого. I 1=1 А, I 2=2 А, I 3=3 А. Указать направления сил, действующих на проводники с токами I 1 и I 2.
1) ®, 2),
3) ®, ® 4), ®
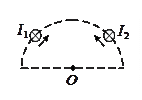
3. В магнитном поле двух бесконечно длинных параллельных прямолинейных проводников с одинаковыми токами пролетает электрон. Куда направлена магнитная сила, действующая на электрон в точке А?
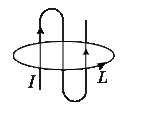 4. Найдите циркуляцию вектора магнитной индукции  по заданному контуру.
| |
5. В однородном магнитном поле в плоскости, параллельной линиям магнитной индукции  , расположена прямоугольная рамка с током. Сравнить работы, необходимые для поворота рамки на угол p/2 вокруг осей а и b.
| 
|
Вариант 2
1. Теорема о циркуляции вектора магнитной индукции. Применение теоремы о циркуляции для расчета поля соленоида и тороида.
2.Два прямолинейных бесконечно длинных проводника с токами расположены взаимно перпендикулярно в одной плоскости. Точки, в которых магнитная индукция равна нулю, располагаются в квадрантах
1) I, II 2) III, IV
3) I, III 4) II, IV
3. Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. Если величину магнитного поля уменьшить в 2 раза, то частота вращения протона
1) увеличится в 2 раза; 2) увеличится в 
раз;
3) не изменится; 
4) уменьшится в 2 раза
4. Найти циркуляцию вектора магнитной индукции по заданному контуру
5. Виток, по которому течет ток силой I = 20 А, свободно установился в однородном магнитном поле с индукцией В =0,016 Тл. Диаметр витка d =10 см. Какую работу надо совершить, чтобы повернуть виток на угол a = p/2 относительно оси, совпадающей с диаметром?
Вариант 3
1. Применение закона Био-Савара-Лапласа для расчета поля, созданного бесконечно длинным прямолинейным проводником.
2. Электрон, влетевший в область однородного магнитного поля, движется по дуге окружности. Как направлен вектор индукции магнитного поля?
3. Частица массы т и заряда q движется по окружности радиуса R в однородном магнитном поле с индукцией В в плоскости, перпендикулярной линиям индукции. Найти кинетическую энергию частицы.
4. По плоскому контуру из тонкого провода течет ток I. Найти магнитную индукцию поля, создаваемого этим током в точке О.
1) 3μоІ/8R 2) μоІ/8R
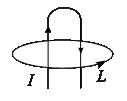3) μоІ/2R 4) μоІ/4R
5. Чему равна циркуляция вектора магнитной индукции по заданному контуру?
Вариант 4
1. Принцип суперпозиции. Применение закона Био – Савара – Лапласа для расчета поля кругового тока.
2. Заряд q >0 движется со скоростью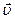 
. Сравнить модули магнитной индукции В в точках 1 и 2:
1) однозначно ответить нельзя 2) В 1< В 2
3) одинаковы 4) В 1 > В 2
3. Частицы, имеющие одинаковые заряды, вылетают из точки А в магнитном поле с одинаковыми скоростями. Максимальная масса соответствует частице
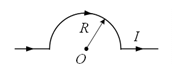1) 1 2) 2 3) 3 4)4
4. Найти индукцию поля в точке О бесконечно длинный проводника с током I показанного на рисунке.
5. В однородное магнитное поле с индукцией 0,1 Тл помещена квадратная рамка площадью 25 см2. Нормаль к плоскости рамки составляет с направлением магнитного поля угол 60о. По рамке течет ток 1 А. Определить вращающий момент, действующий на рамку.
Вариант 5
1. Контур с током в магнитном поле Работа по перемещению контура с током в магнитном поле.
2. В магнитное поле влетает электрон и движется по окружности. По какой траектории будет двигаться протон, влетевший в это поле с такой же скоростью?
3. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу, а ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине. По рамке и проводнику текут одинаковые токи I. Найти силу, действующую на рамку с током.
4. Найти магнитную индукцию поля в точке О.
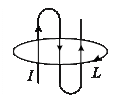
5. Определить циркуляцию вектора магнитной индукции по заданному контуру.
Вариант 6
1. Сила Лоренца. Движение заряженной частицы в перпендикулярном магнитном поле.
2. Магнитное поле создано двумя параллельными длинными проводниками с токами I 1 и I 2, расположенными перпендикулярно плоскости чертежа, причем I 1= I 2. Укажите направление вектора магнитной индукции результирующего поля в точке А, находящейся на одинаковом расстоянии от проводников.
3. Две положительно заряженные частицы движутся во взаимно перпендикулярных направлениях. В тот момент, когда вторая частица оказалась на линии скорости первой, магнитные силы, действующие на частицы равны
1) F1= F2 ≠0 2) F1=0, F2≠0 3) F1≠0, F2=0 4) F1=F2=0
4. Найти магнитную индукцию в точке О.
5. Какую работу совершает однородное магнитное поле с индукцией В =1,5 Тл при перемещении проводника длиной 
=0,2 м, по которому течет ток в 10 А, на расстояние 0,25 м, если направление перемещения перпендикулярно к направлению поля и направлению тока? Проводник расположен под углом a = 30о к направлению поля.
Вариант 7
1. Сила Ампера. Взаимодействие параллельных токов. Магнитная постоянная.
2. По дуге окружности скользят два бесконечно длинных параллельных проводника с токами I 1 = I 2. Как изменится модуль индукции магнитного поля в центре окружности О при сближении проводников?
3. Электрон, пройдя в электрическом поле ускоряющую разность потенциалов U, попадает в однородное магнитное поле, линии индукции которого перпендикулярны направлению движения электрона, и начинает двигаться по окружности. Если ускоряющая разность потенциалов U увеличивается в 2 раза, то радиус окружности
1) увеличится в 2 раза 2) увеличится в 
раз
3) уменьшится в раз 4) уменьшится в 2 раза
 |
4. Найти магнитную индукцию поля, созданного в точке О изогнутым бесконечно длинным проводником с током.
5. Определить циркуляцию вектора магнитной индукции <