Глава 5. МЕТОДЫПРИНЯТИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Теория статистических решений представляет собой теорию выбора оптимального поведения в условиях полной или частичной неопределенности. Современная общая концепция статистического решения принадлежит А.Вальду.
Получение статистических данных всегда связано с проведением эксперимента. Каждый эксперимент имеет стоимость, за которую надо платить. Лицо, принявшее ошибочное решение, также несет потери – с него взыскивается, соответствующий ошибке «штраф». Под оптимальным часто понимается решение, минимизирующее риск – математическое ожидание всех его убытков. В этой постановке любая задача статистического решения может рассматриваться как игра двух участников в смысле Дж. Неймана, в которой одним из игроков является лицо, ответственное за принятие решения, а другим – природа.
Игры с «природой»
В теории игр предполагается, что оба противника (или больше двух) активно противодействуют друг другу, что оба они достаточно умны, чтобы искать и найти свою оптимальную стратегию, и осторожны, чтобы не отступать от нее. Такое положение дает возможность предсказывать поведение игроков.
Неопределенность была лишь в выборе противником конкретной чистой стратегии в каждой отдельной партии. Однако, неопределенность в игре может быть вызвана не сознательным противодействием противника, а незнанием условий, в которых будет приниматься решение, наличием случайных обстоятельств. Такие игры называются играми с "природой".
Игра человека с природой тоже отражает конфликтную ситуацию, возникающую при столкновении интересов в выборе решения. Но стихийным силам "природы" нельзя приписать разумные действия, направленные против человека и тем более какой-либо "злой умысел". Таким образом, корректнее говорить о конфликтной ситуации, вызванной столкновением интересов человека и неопределенностью действий природы.
Действия природы могут наносить ущерб, а могут приносить прибыль. Поведение природы можно оценить статистическими методами, определив присущие ей закономерности. В зависимости от степени знания этих закономерностей, определяющих поведение природы, различаются игры с природой в условиях определенности и игры с природой в условиях неопределенности. В играх первой группы поведение природы известно полностью (задано распределение вероятностей состояний). В играх второй группы – состояния природы не известны.
К явлениям природы, влияющим на результат решения, относят не только погодные и сезонные явления (дождь, засуху, урожай, неурожай), но и проявление любых, не зависящих от нас обстоятельств: например, задержки на транспорте, спрос на продукцию, времена года и др. Поиском решений в таких ситуациях и занимается теория статистических решений.
Человек, играя с природой, стремиться максимизировать свой выигрыш, поэтому, если он осторожный игрок (а теория игр рассматривает именно таких игроков), он должен при выборе своей стратегии руководствоваться тем, что неизвестные или известные ему закономерные действия природы приведут к наименее благоприятным последствиям. Именно поэтому такие игры можно рассматривать как игры двух лиц с нулевой суммой.
Формализация задачи происходит следующим образом: у активного игрока (человека) возможные действия по-прежнему называются стратегиями, а возможные действия пассивного игрока (природы) - состояниями или внешними условиями. В качестве первого игрока всегда выступает человек, поэтому в матрице записывается его выигрыш. Так как нас интересует оптимальная стратегия человека и его гарантированный выигрыш, то в игре достаточно определить максиминную стратегию первого игрока и нижнюю цену игры. Определение верхней цены игры имеет смысл, если данная игра повторяется многократно и оптимальная стратегия может быть смешанной.
Системная матрица
Данные, необходимые для принятия решения в условии неопределенности, обычно задаются в форме матрицы, строки которой соответствуют возможным действиям, а столбцы – возможным состояниям системы.
Пример 1. Для отопления помещения необходимо приобрести уголь. Расход угля и цены на него зависят от погоды в зимнее время (приведены в табл. 6.2).
Таблица 6.2
| Зима | |||
 (мягкая) (мягкая)
|  (нормальная) (нормальная)
|  (суровая) (суровая)
| |
| Расход угля, т | |||
| Цена, руб./т |
Осенью уголь может быть приобретен по минимальной цене 10 руб./т., а излишек неиспользованного угля можно реализовать весной по цене 5 руб./т. Можно избрать одну из трех стратегий в закупке угля: приобрести осенью  – 5т.,
– 5т.,  – 10т.,
– 10т.,  – 18т. Требуется определить оптимальную стратегию в закупке угля.
– 18т. Требуется определить оптимальную стратегию в закупке угля.
Составим, прежде всего, матрицу решений в виде табл. 6.3.
Таблица 6.3
| Стратегии ЛПР (варианты) | Стратегии природы (условия) | ||
 (мягкая) (мягкая)
|  (нормальная) (нормальная)
|  (суровая) (суровая)
| |
 (закупить 5т.) (закупить 5т.)
| -50 | -130 | -310 |
 (закупить 10т.) (закупить 10т.)
| -75 | -100 | -260 |
 (закупить 18т.) (закупить 18т.)
| -115 | -140 | -180 |
Рассмотрим, например, как получен элемент 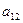 . Если осенью закуплено 5т. угля, то было заплачено 50 руб. в расчете на мягкую зиму. Однако, зима оказалась нормальной, и не хватило еще 5т. угля. Этот уголь можно приобрести зимой, заплатив уже 5·16=80 руб. Таким образом,
. Если осенью закуплено 5т. угля, то было заплачено 50 руб. в расчете на мягкую зиму. Однако, зима оказалась нормальной, и не хватило еще 5т. угля. Этот уголь можно приобрести зимой, заплатив уже 5·16=80 руб. Таким образом, 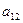 =50+80=130 руб. Аналогично определяются и остальные элементы матрицы решений.
=50+80=130 руб. Аналогично определяются и остальные элементы матрицы решений.
Определим оптимальный вариант в образовании запасов угля для трех стратегий природы:  ,
, 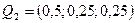 и
и  .
.
Для стратегии  найдем величину среднего выигрыша в зависимости от выбранного варианта
найдем величину среднего выигрыша в зависимости от выбранного варианта  ,
,  или
или  :
:
 :
:  ,
,
 :
:  ,
,
 :
: 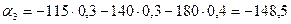 .
.
Аналогично определим средний выигрыш для стратегий природы  и
и  . Результаты расчетов сведем в табл. 6.4.
. Результаты расчетов сведем в табл. 6.4.
Таблица 6.4

| 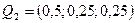
| 
| |

| -178 | -135 | -101 |

| -156,5 | -127,5 | -106,5 |

| -148,5 | -137,5 | -128,5 |
Видим, что максимальный выигрыш для стратегии  равен -148,5, который получится при применении варианта
равен -148,5, который получится при применении варианта  , состоящего в закупке 18 т. угля. Для стратегии
, состоящего в закупке 18 т. угля. Для стратегии  оптимальным является вариант
оптимальным является вариант  , состоящий в закупке 10 т. угля. Для стратегии
, состоящий в закупке 10 т. угля. Для стратегии  оптимальным является вариант
оптимальным является вариант  , состоящий в закупке 5 т. угля. Таким образом, знание состояний природы является существенным для принятия оптимального решения.
, состоящий в закупке 5 т. угля. Таким образом, знание состояний природы является существенным для принятия оптимального решения.
Далее будут рассмотрены различные классические критерии принятия решений.
Пример 2. Станок деревообрабатывающего предприятия в течение месяца приносит прибыль в размере 1000 ден.ед. в случае его безотказной работы. Однако в течение указанного срока эксплуатации станок может выйти из строя, но не более трех раз. Для его ремонта руководство предприятием может не покупать спецоборудования и обойтись для ремонта старым оборудованием, может купить только часть спецоборудования за 30 ден.ед., может купить полный комплект спецоборудования за 60 ден.ед. Если станок выходит из строя, его ремонт без спецоборудавания обходится в 50 ден.ед., с помощью части комплекта спецоборудования – в 25 ден.ед., с помощью полного комплекта спецоборудования – в 10 ден.ед. Известно, что число отказов станка имеет распределение Пуассона с параметром  мес
мес 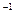 . При этом, если станок выходит из строя более трех раз, стоимость его ремонта остается такой же, как и при трехразовом отказе.
. При этом, если станок выходит из строя более трех раз, стоимость его ремонта остается такой же, как и при трехразовом отказе.
Требуется определить целесообразность приобретения частичного или полного комплекта специализированного ремонтного оборудования.
Предприятие имеет три варианта решения:
 – не покупать спецоборудование,
– не покупать спецоборудование,
 – приобрести часть комплекта спецоборудования,
– приобрести часть комплекта спецоборудования,
 – приобрести полный комплект спецоборудования.
– приобрести полный комплект спецоборудования.
У природы – второго игрока – четыре состояния:
 – станок не откажет,
– станок не откажет,
 – станок откажет один раз,
– станок откажет один раз,
 – станок откажет два раза,
– станок откажет два раза,
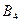 – станок откажет три или более раз.
– станок откажет три или более раз.
Функция выигрыша – прибыль предприятия с учетом затрат на покупку и ремонт станка задается матрицей решений (табл. 6.1).
Таблица 6.1
| Ремонтное оборудование | Выход станка из строя | |||
 (ни разу) (ни разу)
|  (1 раз) (1 раз)
|  (2 раза) (2 раза)
| 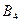 ( ( 3 раз) 3 раз)
| |
 (не покупать) (не покупать)
| ||||
 (купить частично) (купить частично)
| ||||
 (купить полностью) (купить полностью)
|
Элементы матрицы решений получены следующим образом. Например, если приобретен полный комплект ремонтного оборудования (вариант  ) и станок отказал 1 раз (состояние
) и станок отказал 1 раз (состояние  ), то прибыль предприятия за вычетом затрат на покупку и ремонт станка составит
), то прибыль предприятия за вычетом затрат на покупку и ремонт станка составит  ден.ед. Остальные элементы матрицы рассчитываются аналогично.
ден.ед. Остальные элементы матрицы рассчитываются аналогично.
Табл. 6.1 запишем на лист Excel и дополним ее столбцами и строками, как показано в табл. 6.2.
Таблица 6.2
| A | B | C | D | E | F | G | H | I | ||

| 
| 
| 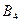
| ММ-критерий | Критерий BL | |||||

| 
| 
| 
| |||||||

| 918,0 | |||||||||

| 929,0 | 929,0 | ||||||||

| 923,6 | |||||||||
| Число отказов | >=3 | |||||||||
| Вероят-ности | 0,165 | 0,298 | 0,268 | 0,269 | ||||||
Максиминный критерий (ММ)
Рассмотрим максиминный (ММ) критерий. В ячейку F3 поместим формулу =МИН(B3: E3), которую скопируем в ячейки F4 и F5.
Максимальное значение блока ячеек F3: F5 равно 910, оно помещается в соответствующей строке столбца G. На основе ММ-критерия следует принять решение  , то есть купить полный комплект ремонтного оборудования.
, то есть купить полный комплект ремонтного оборудования.