Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
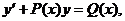 (5.1)
(5.1)
при этом, если правая часть 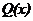 уравнения (5.1) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть
уравнения (5.1) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть 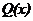 не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.
не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.
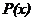 и
и 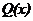 - функции непрерывные на некотором промежутке
- функции непрерывные на некотором промежутке 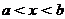 .
.
5.1. Линейные однородные дифференциальные уравнения
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
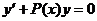 .
.
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.
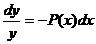 ,
,
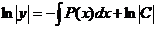 ,
,
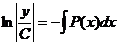
Общее решение:
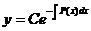
5.2. Линейные неоднородные дифференциальные уравнения
Для интегрирования линейных неоднородных уравнений (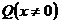 ) применяются в основном два метода: метод Бернулли и метод Лагранжа.
) применяются в основном два метода: метод Бернулли и метод Лагранжа.
5.3. Метод Бернулли.
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций 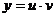 .
.
При этом очевидно, что 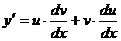 - дифференцирование по частям.
- дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
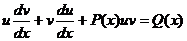 ,
,
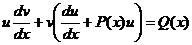 .
.
Далее следует важное замечание – так как первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Например, функция 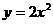 может быть представлена как
может быть представлена как 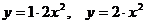 ,
, 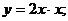 и т.п.
и т.п.
Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение 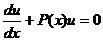 .
.
Таким образом, возможно, получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:
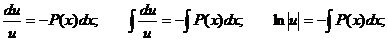
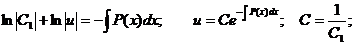
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение 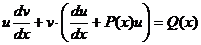 с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю.
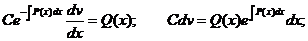
Интегрируя, можем найти функцию v:
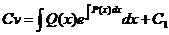
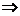
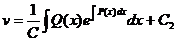 .
.
Т.е. была получена вторая составляющая произведения  , которое и определяет искомую функцию. Подставляя полученные значения, получаем:
, которое и определяет искомую функцию. Подставляя полученные значения, получаем:
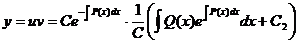
Окончательно получаем формулу:
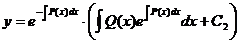 ,
, 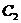 - произвольный коэффициент.
- произвольный коэффициент.
Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
Пример 1. Проинтегрировать дифференциальное уравнение 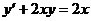 .
.
Решение. Полагаем 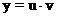 и
и 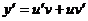 . Подставляем в уравнение
. Подставляем в уравнение 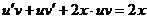 , то есть
, то есть 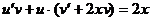 . Полагаем и решаем уравнение
. Полагаем и решаем уравнение  .
.
Разделив переменные 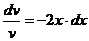 ,
,
интегрируя, находим 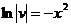 , следовательно
, следовательно 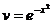 .
.
Постоянную 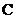 интегрирования не вводим, так как достаточно найти какое-либо решение этого вспомогательного уравнения.
интегрирования не вводим, так как достаточно найти какое-либо решение этого вспомогательного уравнения.
Теперь решаем уравнение для определения u:
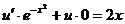 , то есть
, то есть
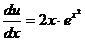 ,
,
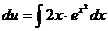 ,
,
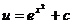 .
.
Итак, общее решение данного уравнения есть 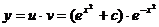 ,
,
то есть 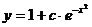 .
.
5.4. Метод Лагранжа
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.
Вернемся к поставленной задаче:
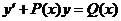
Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.
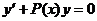
Далее находится решение получившегося однородного дифференциального уравнения:
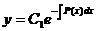 .
.
Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную 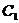 некоторой функцией от х.
некоторой функцией от х.
Тогда по правилам дифференцирования произведения функций получаем:
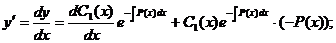
Подставляем полученное соотношение
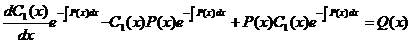 ,
,
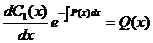 .
.
Из этого уравнения определим переменную функцию 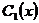 :
:
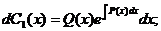
Интегрируя, получаем:
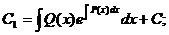
Подставляя это значение в исходное уравнение, получаем:
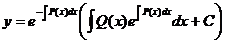 .
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.
Пример 1. Решить уравнение 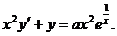
Решение. Сначала приведем данное уравнение к стандартному виду: 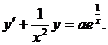
Применим полученную выше формулу: 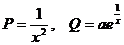 ,
,
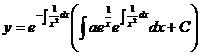 ,
,
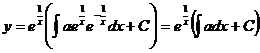 ,
,
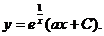
5.5. Уравнение Бернулли
Уравнением Бернуллиназывается уравнение вида
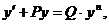 (5.2)
(5.2)
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли (5.2) применяют подстановку 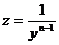 , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Для этого разделим исходное уравнение на 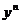 .
.

Применим подстановку, учтя, что 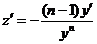 .
.
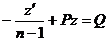 ,
,
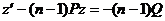 ,
,
Т.е. получилось линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:
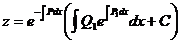 ,
,

Пример 1. Решить уравнение 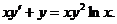
Решение. Разделим уравнение на 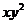 :
: 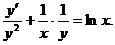
Полагаем 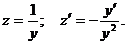
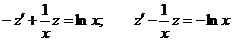 .
.
Полагаем 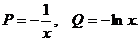
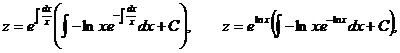
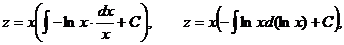
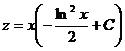 .
.
Произведя обратную подстановку, получаем:
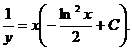
Пример 2. Решить уравнение 
Решение. Разделим обе части уравнения на 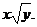
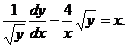
Полагаем 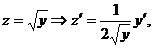 или
или 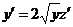 , тогда
, тогда
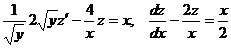 .
.
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
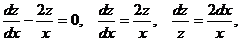
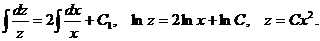
Полагаем  и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
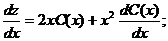
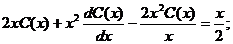
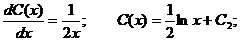
Получаем: 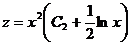 .
.
Применяя обратную подстановку, получаем окончательный ответ:
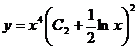 .
.
Вопросы для самоконтроля
1. Линейные дифференциальные уравнения
2. Линейные однородные дифференциальные уравнения
3. Линейные неоднородные дифференциальные уравнения
4. Метод Бернулли.
5. Метод Лагранжа
6. Уравнение Бернулли