Обзор методов решения в Excel

Введение

 

Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области 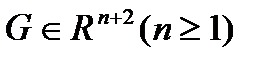и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

Решением этого уравнения на интервале I=[a,b] называется функция u(x).

Решить дифференциальное уравнение у^/=f(x,y) численным методом - это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)

 

Обзор методов решения в Excel

 

1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка

 

Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y' = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

 

yk+1 = yk +(k1 +2k2 +2k3 +k4)/6, (2)

где

k₁ = Fk h = F(xk, yk)h

k₂ = F(xk +h/2, yk +k₁ /2)h

k₃ = F(xk +h/2, yk +k₂ /2)h

k₄ = F(xk +h, yk +k₃)h,

k = 0,..., n-1

h = (xf -x₀)/n (3)

 

1.2 Задача Коши

 

Рассмотрим задачу Коши для уравнений первого порядка на отрезке [a,b]:

 

, (4)

 

Разобьём промежуток [a,b] на N частей . Обозначим, где u(x) –точное решение задачи Коши, и через значения приближенного решения в точках 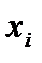. Существует 2 типа численных схем:

1. явные: ) (5)

2. неявные: (6)

 

Здесь F некоторая функция, связывающая приближения. В явных схемах приближенное значение 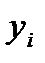в точке 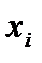определяется через некоторое число k уже определённых приближенных значений. В неявных схемах определяется не рекурентным способом, как в явных схемах, а для его определения возникает уравнение, поскольку равенство (6) представляет из себя именно уравнение на . Явные схемы проще, однако зачастую неявные схемы предпочтительнее

 

1.3 Метод Эйлера

 

Решить дифференциальное уравнение у^/=f(x,y) численным методом - это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что

 

у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀. (7)

Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка (7) с начальным условием

x=x₀, y(x₀)=y₀ (8)

 

Требуется найти решение уравнения (7) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀, х₁, х₂,…, х_n, где x_i=x₀+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В методе Эйлера приближенные значения у(х_i)»y_i вычисляются последовательно по формулам у_i+hf(x_i, y_i) (i=0,1,2…).

При этом искомая интегральная кривая у=у(х), проходящая через точку М₀(х₀, у₀), заменяется ломаной М₀М₁М₂… с вершинами М_i(x_i, y_i) (i=0,1,2,…); каждое звено М_iM_i+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (7), которая проходит через точку М_i. Если правая часть уравнения (7) в некотором прямоугольнике R{|x-x₀|£a, |y-y₀|£b}удовлетворяет условиям:

 

|f(x, y₁)- f(x, y₂)| £ N|y₁-y₂| (N=const), (9)

|df/dx|=|df/dx+f(df/dy)| £ M (M=const),

 

то имеет место следующая оценка погрешности:

 

|y(x_n)-y_n| £ hM/2N[(1+hN)ⁿ-1], (10)

 

где у(х_n)-значение точного решения уравнения (7) при х=х_n, а у_n- приближенное значение, полученное на n-ом шаге.

Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. Погрешность более точного значения у_n^* оценивается формулой

 

|y_n-y(x_n)|»|y_n^*-y_n|. (11)

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

 

1.4 Модифицированный метод Эйлера

 

Рассмотрим дифференциальное уравнение (7) y^/=f(x,y) с начальным условием y(x₀)=y₀. Разобьем наш участок интегрирования на n равных частей. На малом участ интегральную кривую заменим прямой линией.

 

Рисунок 1 Метод Эйлера в графическом виде

 

Получаем точку М_к(х_к,у_к). Через М_к проводим касательную:

 

у=у_к=f(x_k,y_k)(x-x_k)

 

Делим отрезок (х_к,х_к1) пополам

x_Nk^/=x_k+h/2=x_k+1/2 (12)

y_Nk^/=y_k+f(x_k,y_k)h/2=y_k+y_k+1/2

 

Получаем точку N_k^/. В этой точке строим следующую касательную:

 

y(x_k+1/2)=f(x_k+1/2, y_k+1/2)=α_k (13)

 

Из точки М_к проводим прямую с угловым коэффициентом α_к и определяем точку пересечения этой прямой с прямой Х_к1. Получаем точку М_к^/. В качестве у_к+1 принимаем ординату точки М_к^/. Тогда:

 

у_к+1=у_к+α_кh

x_k+1=x_k+h

α_k=f(x_k+h/2, y_k+f(x_k,Y_k)h/2) (14)

y_k=y_k-1+f(x_k-1,y_k-1)h (14)

 

(14)-рекурентные формулы метода Эйлера.

Сначала вычисляют вспомогательные значения искомой функции у_к+1/2 в точках х_к+1/2, затем находят значение правой части уравнения (11) в средней точке y^/_k+1/2=f(x_k+1/2, y_k+1/2) и определяют у_к+1.

Для оценки погрешности в точке х_к проводят вычисления у_к с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:

 

| у_к^*-у(х_к)|=1/3(y_k^*-y_k), (15)

 

где у(х)-точное решение дифференциального уравнения.

Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y^//=f(y^/,y,x) c начальными условиями y^/(x₀)=y^/₀, y(x₀)=y₀, выполняется замена

y^/=z (16)

z^/=f(x,y,z)

 

Тем самым преобразуются начальные условия

 

y(x₀)=y₀, z(x₀)=z₀, z₀=y^/₀ (17)

 

1.5 Практическая часть

 

Здесь решается уравнение dy/dx = 2x-y+x² на интервале [0,2], начальное значение y(0)=0, для оценки точности задано также точное решение в виде функции u(x)=x². Оценка погрешности делается в нормеL₁, как и принято в данном случае

 

Рисунок 2