Для решения задачи 3 см. [5] глава 1. § 1—5.
ЗАДАЧА 3.
Наскладе университетахранится 28 одинаковых упаковок писчейбумаги. Известно, что в четырехиз нихсодержитсябумага более низкого качества. Случайнымобразомвыбирают три упаковкибумаги, Вычислить вероятность того, что среди них;
А)нет упаковок с бумагой более низкого качества,
Б) есть однаупаковкатакой бумаги.
Решение.
Рассмотрим два случайных события:
А – среди взятых трех упаковок нет упаковок с бумагой более низкого качества;
В - среди взятых трех упаковок есть однаупаковкас бумагой более низкого качества (и, следовательно, две – с бумагой более высокого качества).
Общеечисло возможныхэлементарныхисходов для данных испытанийравно числуспособов, которымиможноизвлечь 3 упаковки бумаги из28 упаковок, то есть
= 
= 
= 
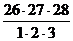=13·9·28=3276 – числу сочетаний из 28 элементов по 3.
а)Подсчитаемчисло исходов, благоприятствующих интересующему нас событию (нет упаковокс бумагой более низкого качества). Это число исходов ровно числуспособов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть
= 
= 
= 
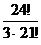=11·23·8=2024
искомая вероятностьравна отношению числа исходов, благоприятствующихсобытию А, к числу всех элементарных исходов:
Р(А) = 
= 
≈0,62
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковокбумаги ровно 1 упаковкасодержитбумагу болеенизкого качества): две упаковкиможно выбрать из 24 упаковок: 
= 
= 
= 
=276 способами, при этом одну упаковку нужно выбирать из четырех: 
= 
= 
=4 способами. Следовательно,число благоприятствующих исходов равно 
· =276·4=1104
Искомая вероятность равна отношению числа исходов, благоприятствующих событию В, к числу всехэлементарныхисходов Р(В) = 
= 
≈0,34
Ответ: а)Р(А) =0,62;б) Р(В)=0,34.
ЗАДАЧА 4.
Магазинполучает электролампочкис двух заводов, причем доля первого завода составляет 25 %. Известно, чтодоля брака на этих заводах равна соответственно5 % и 10 % от всей выпускаемой
продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?
Решение: Обозначим черезАсобытие - « лампочкаокажетсябракованной ». Возможны следующие гипотезы о происхождении этой лампочки: H1 - «лампочка поступила с первого завода ». H2 - «лампочка поступила со второгозавода ». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равнысоответственно p(H1)= 
= 0,25; p(H2) = 
=0,75.
Условная вероятность того, что бракованнаялампочка выпущенапервымзаводом – p(A/H1) = 
=0,05, вторымзаводом- p(A/H2) = 
=0,10 искомую вероятностьтого, что продавец взял бракованную лампочку, находим по формуле полной вероятности
р(А) = P(H1)· p(A/H1)+P(H2)·(A/H2)= 0,25·0,05+0,75·0,10=0,0125+0,075=0.0875
Ответ: р(А) = 0,0875.
Для решениязадачи5 см. [5]глава6 § 1—3, глава 7 § 1-2, глава8 § J—3.
ЗАДАЧА 5.
Задан закон распределения дискретной случайной величены X:
|
Найти:
а) неизвестную вероятность р.
б) математическое ожидание М, дисперсию D исреднее квадратическоеотклонение σ данной случайной величины;
в) функцию распределения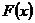 
и построить её график;
г) закон распределения случайной величины 
, если её значения заданы функциональной зависимостью 
Решение:
а) так как сумма всех, вероятностей должна равняться единице, тополучим уравнение
0,05- p + 0,12 + 0,23-0,32 + 0,14+0,04 = 1.
Отсюда р + 0,9 = 1и р= 0,1.
б)Математическое ожидание М это сумма всех произведенийзначенийслучайной величины на их вероятности:
М = (-4)·0,05+(-2)·0,1 + 0·0,12 + 2·0,23 + 4·0,32 + 6·0,14 + +8·0,04-0,2-0,2+0 + 0,46 + 1,28 + 0,84 + 0.32 = -0,4 + 2,9 = 2,5.
Дисперсия 
= (-4)·0.05+(-2)2·0,1+02·0,12+22·0,23+42·0,32+62·0,14+82·0,04-(2,5)2=
=0,8+0+0,92+5,12+5,04+2,56-6,25=8,59
Среднее квадратическое отклонение σ = 
= 
≈2,9.
Если 
Если 
Если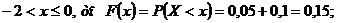 
Если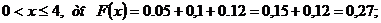 
Если 
Если 
Если 
Если 
Итак, функция распределения может быть записана так:
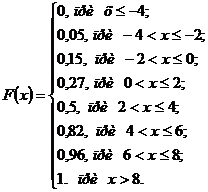
График этой функции приведен на рисунке:
г) Сначала найдем значения случайной величины .
По условиям задачи 
Поэтому 
Составим таблицу вида:
| Y | -1 | ||||||
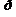
| 0,05 | 0,1 | 0,12 | 0,23 | 0,32 | 0,14 | 0,04 |
Чтобы получить закон распределения случайной величины необходимо:
1) рассмотреть её значения;
2) сложить вероятности, соответствующие совпадающим значениям данной таблицы.
Итак, закон распределения случайной величины :
| Y | -1 | ||||
| P | 0,12 | 0,33 | 0,37 | 0,14 | 0,04 |
Для решения задачи 6 см. [5] глава 5, § 2, § 3.
ЗАДАЧА 6.
Известно, что вероятность положительного исхода некоторого опыта равна 0,125. Найдите вероятность того, что в серии из 128 опытов положительный исход произойдет
а) в 20 опытах
б) от 12 до 20 опытов.
Решение:
а) воспользуемся локальной теоремой Лапласа. Вероятность того, что в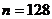 
испытаниях, в каждом из которых вероятность появления события равна 
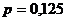,равна 
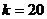раз (безразлично, в какой последовательности) приближенно равна
Так как 
.
Значение функции 
находим в таблице (см. например, [5], стр. 461): 
Итак, 
Отметим, что таблица функции 
приведена только для положительных значений. Если же значение х получилось отрицательным, точки знак минус можно просто опустить в силу четности функции .
б) воспользуемся интегральной теоремой Лапласа. Вероятность того, что в 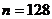независимых испытаниях событие наступит от 
до 
раз приближенно равна
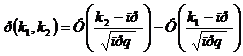
Так как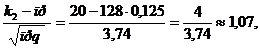 
,
где 
Значение функции 
также находим в специальной таблице (см. например [5], стр. 389). В таблице 
. Для отрицательных значений х используют эту же таблицу, учитывая, что является нечетной функцией, то есть 
. Итак, 
Отсюда
Ответ: 
Вопросы к экзамену (за два семестра)
1. Системы линейных уравнений, основные понятия Решение систем линейных алгебраических уравнений методом Крамера, Гаусса и с помощью обратной матрицы.
2. Векторы и линейные операции над ними. Арифметическое п -мерное векторное пространство Rn Геометрический смысл пространств R2 и R3.
3. Скалярное произведение векторов и его свойства. Длина вектора, угол между векторами.
4. Линейно зависимые и линейно независимые системы векторов.
5. Базис пространства. Разложение вектора по произвольному базису.
6. Различные виды уравнения прямой на плоскости. Угол между прямыми.
7. Прямая и плоскость в пространстве.
8. Основная задача линейного программирования. Геометрический метод решения задачи ЛП с двумя переменными.
9. Основные понятия теории вероятностей. Операции над событиями.
10. Аксиоматическое построение теории вероятностей. Классическая вероятностная схема.
11. Элементы комбинаторики и вычисление вероятности событий. Геометрическая вероятность.
12. Теорема сложения вероятностей.
13. Условная вероятность. Независимость событий. Теорема умножения вероятностей.
14. Формула полной вероятности.
15. Формула Бейеса.
16. Вероятность событий в схеме Бернулли.
17. Локальная и интегральная теоремы Муавра - Лапласа.
18. Определение случайной величины. Функция распределения и ее свойства.
19. Ряд распределения, полигон и функция распределения дискретной случайной величины.
20. Плотность распределения и функция распределения случайной величины.
21. Математическое ожидание дискретной и непрерывной величины.
22. Дисперсия и среднее квадратическое отклонение случайной непрерывной величины.
23. Распределения дискретных случайных величин: биномиальное, Пуассона. Их числовые характеристики.
24. Равномерное и показательное распределения, характеристики.
25. Нормальное распределение и его числовые характеристики.
26. Понятие случайного вектора на примере системы двух случайных величин. Закон распределения системы двух дискретных случайных величин. Условные законы распределения. Независимые случайные величины.
27. Числовые характеристики системы случайных величин.
28. Предельные теоремы теории вероятностей.
29. Функция и ее способы задания. Элементарные и неэлементарные функции.
30. Числовая последовательность и ее предел.
31. Предел функции. Свойства пределов.
32. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых.
33. Виды неопределенности и способы раскрывания неопределенностей. Замечательные пределы.
34. Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных на отрезке.
35. Непрерывность функции в точке и на отрезке. Классификация точек разрыва.
36. Производная, ее геометрический, физический и экономический смысл.
37. Основные правила дифференцирования. Уравнение касательной к графику функции.
38. Основные теоремы дифференциального исчисления: теорема Ферма, теорема Ролля.
39. Основные теоремы дифференциального исчисления: теорема Лагранжа, теорема Коши.
40. Правило Лопиталя. Дифференциал функции и его применение к приближенным вычислениям.
41. Производные и дифференциалы высших порядков.
42. Необходимое и достаточные условия экстремума функции одной переменной.
43. Выпуклость, вогнутость и точки перегиба графика функции. Асимптоты.
44. Общая схема исследования функции одной переменной.
45. Разложение функции одной переменной в ряды Тейлора и Маклорена.
46. Функция нескольких переменных. Предел и непрерывность.
47. Частные производные функции нескольких переменных. Производные высших порядков
48. функции нескольких переменных.
49. Производная по направлению функции нескольких переменных. Дифференциал функции нескольких переменных. Градиент.
50. Экстремум функции двух переменных..
51. Условный экстремум функции нескольких переменных.
52. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.
53. Метод замены переменной и формула интегрирования по частям для неопределенного интеграла.
54. Задача о нахождении площади криволинейной трапеции. Определенный интеграл.
55. Свойства определенного интеграла.
56. Формула Ньютона-Лейбница. Определенное интегрирование заменой переменной и по частям.
57. Приложения определенного интеграла к решению геометрических задач. Приближенное вычисление определенных интегралов.
58. Несобственные интегралы.
59. Кратные интегралы.
60. Задачи, приводящие к понятию дифференциального уравнения.
61. Дифференциальные уравнения первого порядка: основные определения и теоремы.
62. Дифференциальные уравнения первого порядка с разделяющимися переменными.
63. Однородные дифференциальные уравнения первого порядка.
64. Линейные дифференциальные уравнения первого порядка.
65. Дифференциальные уравнения второго порядка: основные определения. Дифференциальные уравнения, допускающие понижение порядка (1 тип).
66. Дифференциальные уравнения, допускающие понижение порядка (2 и 3 тип).
67. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами: основные определения. Теорема о структуре общего решения. Решение однородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
68. Решение неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами с правой частью вида f(x) = Рп (х).
69. Решение неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами с правой частью вида f(x) = Рп(х)-еах.
70. Решение неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами с правой частью вида f(x)= eax(Mcosβx + Nsinβx).
71. Числовые ряды: основные определения. Необходимый признак сходимости знакоположительного числового ряда.
72. Необходимый признак сходимости знакоположительного числового ряда. Достаточные признаки сходимости знакоположительного числового ряда: признаки сравнения, признак Даламбера.
73. Достаточные признаки сходимости знакоположительного числового ряда: радикальный и интегральный признаки Коши, признак Даламбера.
74. Знакочередующиеся числовые ряды. Теорема Лейбница. Понятие абсолютной и условной сходимости.
75. Понятие функционального ряда. Степенные ряды: основные определения.
76. Нахождение области сходимости степенного ряда.
77. Разложение элементарных функций в степенные рады.
78. Использование рядов для приближенных вычислений.