ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
1.8.5. Канонические уравнения поверхностей второго порядка.
1.8.6. Сфера. Эллипсоид.
1.8.7. Однополостный гиперболоид.
1.8.8. Двуполостный гиперболоид.
1.8.9. Конус.
1.8.10. Эллиптический параболоид.
1.8.11. Гиперболический параболоид.
1.8.12. Цилиндры.
Канонические уравнения поверхностей второго порядка.
В зависимости от значений коэффициентов уравнения второй степени
| Ax2+By2+Cz2+Dx+Ey+Fz+G=0, | (1.8.16) |
в котором коэффициенты A, B, C одновременно не обращаются в нуль, может определять поверхность второго порядка (цилиндрическую, коническую, эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический параболоид, гиперболический параболоид, сферу), плоскость, две пересекающиеся плоскости, две параллельные плоскости, точку и, наконец, может не определять никакой поверхности.
Для того, чтобы определить, какую поверхность определяет уравнение (1.8.16) при заданных численных значениях коэффициентов, пользуются методом выделения полных квадратов (МВПК).
По методу выделения полных квадратов группируют члены, содержащие x2 и x, (y2 и y, z2 и z).
Коэффициенты при x2, y2 , z2 выносят за скобки и выражения, содержащиеся в скобках дополняют до полного квадрата. Разделив обе части на свободный член, получают каноническое уравнение поверхности.
Приведем канонические уравнения поверхностей.
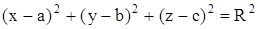
| Сфера. |
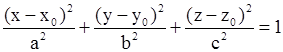
| Эллипсоид. |
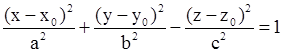
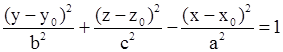
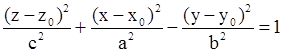
| Однополостный гиперболоид |
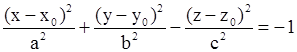
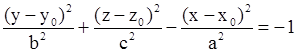
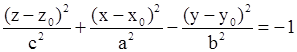
| Двуполостный гиперболоид. |
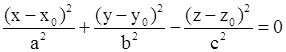
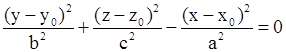
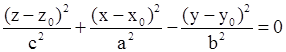
| Конус. |
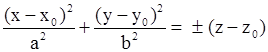
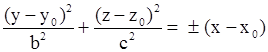
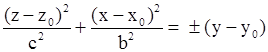
| Эллиптический параболоид. |
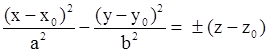
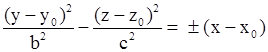
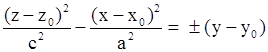
| Гиперболический параболоид. |
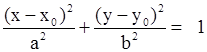
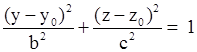
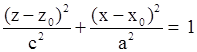
| Эллиптический цилиндр, образующая параллельна оси OZ Эллиптический цилиндр, образующая параллельна оси OX Эллиптический цилиндр, образующая параллельна оси OY |
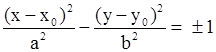
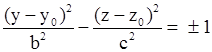
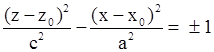
| Гиперболический цилиндр, образующая параллельна оси OZ Гиперболический цилиндр, образующая параллельна оси OX Гиперболический цилиндр, образующая параллельна оси OY |
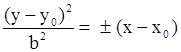
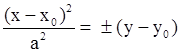
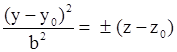
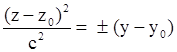
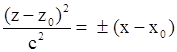
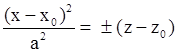
| Параболический цилиндр, образующая параллельна OZ Параболический цилиндр, образующая параллельна OZ Параболический цилиндр, образующая параллельна OX Параболический цилиндр, образующая параллельна OX Параболический цилиндр, образующая параллельна OY Параболический цилиндр, образующая параллельна OY |
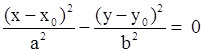
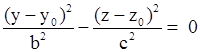
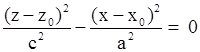
| Две пересекающиеся плоскости |
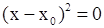
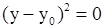
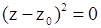
| Две совпадающие плоскости |
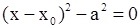
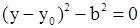
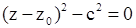
| Две параллельные плоскости (в этом случае каноническое уравнение получают делением обеих частей на коэффициент при полном квадрате. |
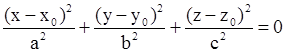
| Точка |
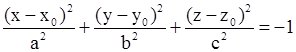
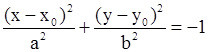
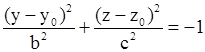
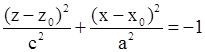
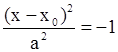
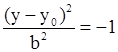
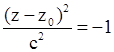
| Не определяет никакой поверхности |
Сфера. Эллипсоид.
Сфера
Каноническое уравнение сферы с центром в точке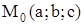 
и радиусом R в декартовой системе координат имеет вид (рис.1.8.14):
|
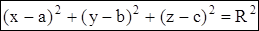
| Рис.1.8.14 |
Эллипсоид.
Каноническое уравнение эллипсоида с полуосями a,b,c (a>0, b>0, c>0) имеет вид:
.
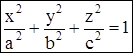Из канонического уравнения эллипсоида видно, что координаты точек поверхности ограничены: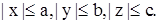 
. Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат.
Для изучения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью XOY. Так как любая точка плоскости имеет нулевую аппликату z=0, то координаты точек эллипсоида на плоскости удовлетворяют уравнению
.
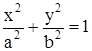Аналогично, сечение в плоскости YOZ дает эллипс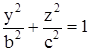 
с полуосями b и c, а сечение плоскостью XOZ – эллипс 
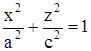с полуосями a и c (рис.1.8.15)
Рис.1.8.15.
Построенный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью z = h. Эта плоскость параллельна плоскости XOY. Уравнения этой линии пересечения
.
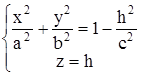Очевидно, что если |h|>c, то ни одна точка пространства не может удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой- отрицательное. Если |h|=c, то в сечении получим лишь одну точку (0;0;c) или(0;0;-c) в зависимости от знака h.
Пусть |h|<c. Тогда исходное уравнение преобразуем к виду
.
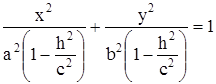Введём обозначения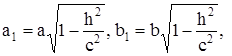 
тогда уравнение примет вид:
.
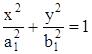Данное уравнение является уравнением эллипса, подобного эллипсу, задаваемому уравнением, полученным при пересечении эллипсоида плоскостью с коэффициентом подобия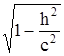 
и полуосями 
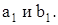Ясно, что сечение плоскостью z = -h является таким же эллипсом, расположенным симметрично первому относительно плоскости. Изобразим эти сечения (рис.1.8.16, рис.1.8.17).
Рис.1.8.16.
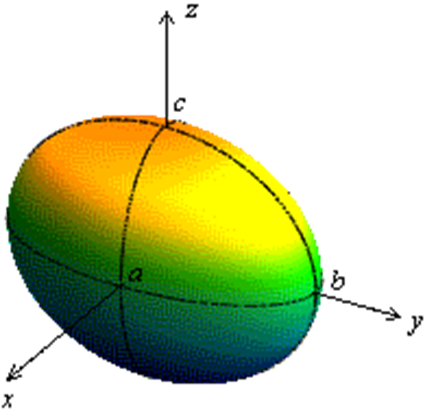
Рис.1.8.17.
Однополостный гиперболоид.
Каноническое уравнение однополостного гиперболоида имеет вид:
.
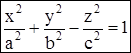Исследуем форму однополостного гиперболоида. Так же, как эллипсоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью XOY. На этой плоскости z=0, поэтому уравнение линии пересечения с данной плоскостью:
.
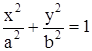Это уравнение на плоскости задает эллипс с полуосями a и b.
Найдем линию пересечения с плоскостью YOZ. На этой плоскости x = 0, поэтому
.
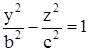Это уравнение гиперболы на плоскости YOZ, где действительная полуось равна b, а мнимая полуось равна c. Построим эту гиперболу (рис.1.8.18).
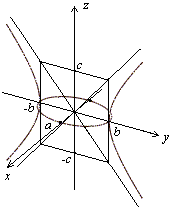
Рис 1.8.18.
Сечение плоскостью XOZ также является гиперболой с уравнением
.
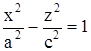Изобразим и эту гиперболу. Найдем линии пересечения поверхности с плоскостями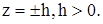 
. Уравнения этих линий
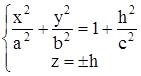
Первое уравнение преобразуем к виду:
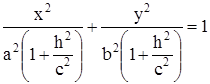
Введём обозначения: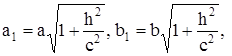 
тогда уравнение примет вид: 
.
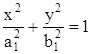Данное уравнение является уравнением эллипса, подобного эллипсу в плоскости XOY, с коэффициентом подобия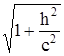 
и полуосями 
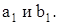(рис.1.8.19,1.8.20,1.8.21).
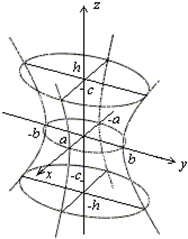
Рис. 1.8.19.
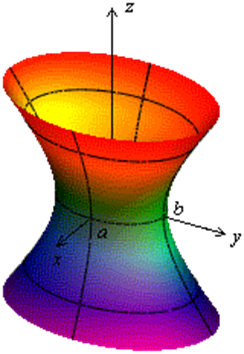
Рис.1.8.20.
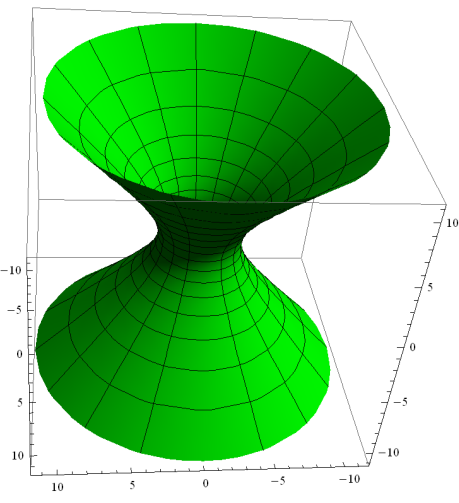
Рис.1.8.21.