Линейные пространства
1. Дайте определение линейного пространства. Приведите примеры линейных пространств.
Опр. Линейное пространство - это множество элементов, для которого определены операции сложения векторов и умножения вектора на число. Указанные операции должны удовлетворять следующим условиям:
1) a + b = b + a
2) (a + b)+c = a+(b + c)
3) a + 0 = a
4) a + (-a) = 0
5) k (a + b) = ka + kb
6) (k + m) a = ka + ma
7) k(ma) = (km)a
8) 1*a = a
Где a, b, c – произвольные векторы;
k, m – произвольные действительные числа
Примеры линейных пространств:
1) пространство Rn;
2) множество решений однородной системы линейных уравнений;
3) множество функций, определенных на отрезке [a;b], с заданными для них обычным образом операциями сложения и умножения на число;
4) множество положительных чисел, если операцию сложения двух элементов x и y определить как их произведение (понимаемое в обычном смысле), а операцию умножения х на действительное число k - как возведение x в степень k;
5) множество всех многочленов с заданными для них стандартным образом операциями сложения и умножения на число;
6) множество всех многочленов, степень которых не превышает n.
2. Дайте определение линейно зависимой системы векторов. Приведите примеры. Будет ли линейно зависима система, включающая нулевой вектор? Ответ обоснуйте.
Система векторов а1, а2 и аm называется линейно зависимой, если существуют такие числа с1, с2, сm (не равные нулю одновременно) и выполняется равенство:
с1ā1+с2ā2+...+сmām =0.
Пример:
а1 = (2, 2, 3)
а2 = (0, -4, 5)
а3 = (3, 13, -8) – система векторов.
Пусть с1 = 3, с2 = -5, с3 = -2, тогда 3а1 - 5а2 - 2а3 = (6, 6, 9) – (0, -20, 25) – (6, 26, -16) = (0, 0, 0)
Вывод: система векторов линейно зависимая.
Утверждение: Если часть системы линейно зависима, то и вся система линейно зависима.
Следствие: Система, включающая нулевой вектор, линейно зависима.
Док-во: Пусть дана система из трех векторов а1, а2, а3, причем часть системы, состоящая из векторов а2, а3 – линейно зависима, т. е. справедливо равенство:
с2 а2 + с3 а3 = 0; с2, с3 ≠ 0.
Добавим к обеим частям нулевой вектор а1, получим:
0а1 + с2 а2 + с3 а3 = 0, что означает линейную зависимость такой системы.
1. Система из одного вектора а линейно зависима тогда когда а=0
2. Система содержащая более одного вектора линейно зависима в том и только в том случае когда среди данных векторов имеется такой который линейно выражается через все остальные
3. Если часть системы линейно зависима то и вся система линейно зависима, система включающая нулевой ветор линейно зависима
4. Если система линейно независима но при добавлении к ней а становится зависимой то а линейно выражается через другие векторы
3. Дайте определение линейно независимой системы векторов. Приведите примеры. Будет ли линейно независимой лестничная система векторов? Ответ обоснуйте.
Система векторов ā1,ā2,…,ām такова, что равенство с1ā1+с2ā2+...+сmām =0 возможно только при с1=c2=,..,=с3=0, то эта система называется линейно независимой.
Пример:
а = (а1, а2, …, аn)
b = (0, b2,…, bn)
c = (0, 0, c3, …, cn) – лестничная система векторов.
Любая лестничная система векторов линейно независима.
Док-во: От противного. Предположим, что лестничная система векторов линейно зависима. Тогда один из данных векторов должен линейно выражаться через остальные. Пусть а выражается через b и c. Тогда:
а = kb + mc
Но такое равенство невозможно, так как первая координата вектора а отлична от нуля, а первая координата вектора kb + mc равна нулю. Данное противоречие доказывает, что система векторов а, b, c – линейно независима.
Примеры:
ü Система векторов ·i, j линейного пространства R2 геометрических радиусов векторов плоскости линейно независима.Действительно.
i = (1, 0), j = (0, 1), С1·i + С2· j = (С1, С2), а из (С1, С2) = 0 следует, что С1 = 0 и С1 = 0, т.е. система векторов i, j из R2 линейно независима.
ü В линейном арифметическом пространстве Rn рассмот-
рим n векторов e 1 = (1, 0,..., 0), e 2 = (0, 1,..., 0, 0),..., e n = (0, 0,.., 0, 1). До-
кажем, что система этих векторов линейно независима.
Так как для любых коэффициентов α1, α2,..., αn линейная комбина-
ция α1 e 1 + α2 e 2 +... + αn e n = (α1, α2,..., αn), то ясно, что она может быть
равна нулевому вектору (0, 0,..., 0) только при условии равенства нулю
всех коэффициентов. По определению, это означает, что система векторов
линейно независима.
4. Дайте определение базиса линейного пространства. Докажите, что координаты вектора в данном базисе определены однозначно.
Система векторов а1, а2, …, аn называется базисом линейного пространства V, если выполнены следующие условия:
1) эти векторы линейно независимы;
2) любой вектор а из V является линейной комбинацией векторов данной системы, т. е.
а = k1 а1 + k2 а2 + … + kn аn
Предложение: координаты вектора в данном базисе определены однозначно.
Док-во: пусть существует два разложения данного вектора а по базису а1, а2, …, аn
а = k1 а1 + k2 а2 + … + kn аn
а = l1 а1 + l2 а2 + … + ln аn
Так как левые части равны, то правые также равны:
k1 а1 + k2 а2 + … + kn аn = l1 а1 + l2 а2 + … + ln аn
(k1 - l1) а1 + (k2 - l2) а2 + …+ (kn - ln) аn = 0
Так как векторы базиса линейно независимы, то k1 - l1 = 0 → k1 = l1
ч. т. д.
5. Что называется размерностью линейного пространства 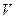 ? Может ли система из
? Может ли система из 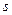 векторов, где
векторов, где 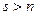 , являться базисом
, являться базисом 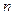 - мерного пространства
- мерного пространства 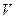 ? Ответ обоснуйте.
? Ответ обоснуйте.
Размерностью пространства V называется число векторов его базиса. Размерность пространства V обозначается через dimV. Линейное пространство, имеющее размерность n, называют n-мерным.
В n-мерном пространстве V любая система из s векторов, где s>n, линейно зависима. А из определения базиса линейного пространства следует, что система векторов должна быть линейно независима. Следовательно, система из s векторов, где s>n, не может являться базисом n-мерного пространства V.
6. Пусть 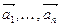 - векторы из
- векторы из 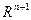 . Можно ли составить базис пространства
. Можно ли составить базис пространства 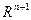 из линейных комбинаций этих векторов? Ответ обоснуйте.
из линейных комбинаций этих векторов? Ответ обоснуйте.
Нет. Размерность Н + 1, следовательно число векторов – 1.
7. Дайте определение подпространства линейного пространства и приведите пример. Как связаны размерности пространства и его подпространства? Ответ обоснуйте.
Подпространством линейного пространства R над полем K называется любое непустое подмножество M этого пространства, на котором корректны операции сложения элементов и умножения элемента на число, которые введены в исходном линейном пространстве R.
Примеры подпространств:
1 Прямая (подпространство) на плоскости (пространство)
2 Плоскость (подпространство) в пространстве R3 (пространство)
3 Все матрицы вида ab, a = -d, подпространство пространства всех
c-a матриц 2х2
Одно из свойств подпространств говорит о том, что размерность подпространства не превосходит размерности самого пространства (так как подпространство является подмножеством пространства).
Теор. Подпр-во является линейным пр-вом
1) Для любых двух векторов а, в, из S их сумма также принадлежит лин пространству
2) Произведение а на действительное число тоже принадлежит данному пространству
Размерность родпростарнства S (неравно 0) меньше пр-ва V. Если бы их размерность была равна, то базис подпространства S являлся бы базисом V, Следовательно S и V совпали бы.
8. Какие из множеств, образованных всевозможными векторами 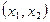 из
из 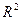 такими, что а)
такими, что а) 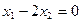 , б)
, б) 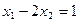 , в)
, в) 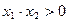 , являются подпространствами в
, являются подпространствами в 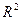 , а какие нет? Ответ обоснуйте.
, а какие нет? Ответ обоснуйте.
а) задает подпространство M, так как это уравнение определяет прямую (одномерное подпространство) на плоскости, проходящее через (0,0) и для него выполнены условия подпросранства.
б) не задает подпространства, так как нарушается 2ое условие: Пример: x = (1, 0) 2 M.
При этом 2 · x = (2, 0) не принадлежит M.
в) не задает подпространства, так как нарушается первое условие
Системы линейных уравнений
9. Какие системы уравнений называются определенными, неопределенными, несовместными? Приведите примеры. Может ли однородная система линейных уравнений быть несовместимой?
Определенная система – система линейных уравнений, имеющая одно решение
Неопределенная система – система линейных уравнений, имеющая более одного решения
Несовместная система – система линейных уравнений, не имеющая ни одного решения.
Если правые части системы равны нулю, то такая система называется однородной. Любая однородная система совместна: нулевые значения неизвестных составляют ее решения.
Решением СЛАУ является любой набор значений неизвестных: Х1 = a 1, Х2 = a 2, …., Х1 = a n, удовлетворяющий всем уравнениям системы.
Если существует хотя бы одно решение системы – она совместна. Система, не имеющая ни одного решения, называется несовместной (появление противоречивой строки)
Например:
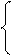 2*х1 + 3*х2 + х3 - 2*х4 =9
2*х1 + 3*х2 + х3 - 2*х4 =9
7*х1 + 8*х2 – х3 - 2*х4 =5
3*х1 + 2*х2 - 3*х3 + 2*х4 =10
Линейное уравнение называется однородным, если свободный член уравнения равен нулю. Система, состоящая из однородных уравнений, называется однородной.
Например:
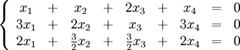
Если система совместна, то она может иметь единственное решение, и в этом случае ее называют определенной.
Например: (имеет единственное решение)
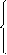 х1+2*х2+3*х3=7
х1+2*х2+3*х3=7
2*х1-х2+х3=4
3*х1-2*х2-х3=3
Систему называют неопределенной, когда она имеет бесконечно много решений (если число переменных больше, чем количества уравнений)
!!Любая однородная система совместна!!
10. Докажите, что однородная система, состоящая из трех уравнений от пяти переменных, имеет бесконечно много решений.
Решим систему относительно х1,х2,х3.  .
.
Каждый раз меняя значения, мы будем получать разные решения.
11. Докажите, что множество решений однородной системы из  уравнений с
уравнений с 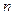 неизвестными является подпространством пространства
неизвестными является подпространством пространства 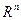 . Какова размерность этого подпространства? Ответ обоснуйте.
. Какова размерность этого подпространства? Ответ обоснуйте.
12. Как связаны решения совместной неоднородной системы линейных уравнений 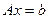 и однородной системы
и однородной системы 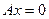 ? Приведите пример.
? Приведите пример.
Теорема (Кронекера и Капелли): Неоднородная система уравнений Ax = b сов-
местна тогда и только тогда, когда rangA = rangB (где B - расширенная матрица системы (B = [A|b]), получающаяся из A дописыванием свободного столбца b).
13. Дайте определение фундаментального набора решений однородной системы линейных уравнений. Приведите пример системы и найдите ее фундаментальный набор решений.
Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. Называется базисное пр-во решений линейной однородной системы ур-й. Для того, чтобы построить фундаментальный набор решений однородной СЛАУ при помощи метода Гаусса, необходимо решить систему по этому методу и выразить базисные неизвестные через свободные. Далее, присваивая одной свободной неизвестной значение 1, а остальным 0, получим фундаментальное решение. Повторяя эту операцию со всеми свободными неизвестными, получим фундаментальный набор решений.
14. Найдите фундаментальный набор решений системы: 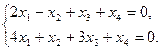
15. Пусть дан фундаментальный набор решений некоторой однородной системы: 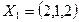 ,
, 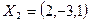 . Укажите другой фундаментальный набор решений этой системы. Ответ обоснуйте.
. Укажите другой фундаментальный набор решений этой системы. Ответ обоснуйте.
Любое другое решений – это линейная комбинация двух уже известных решений.
Евклидовы пространства
16. Дайте определение скалярного произведения в пространстве 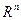 . Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.
. Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.
На линейном пространстве V задано скалярное произведение, если любым двум векторам а и b из V сопоставляется число (а, b) – их скалярное произведение так, что выполняются следующие условия:
1) (a, b) = (b, a)
2) (ka, b) = k(a, b)
3) (a + b, c) = (a, c) + (b, c)
4) (a, a) ≥ 0 и (a, a) = 0, только если а = 0.
Для любых двух векторов евклидова пространства справедливо неравенство Коши-Буняковского:
І(а, b)І ≤ ІaІ ІbІ
Скалярным произведением векторов х,у принадлеж. R n: x=(x1,…,xn), y=(y1,…yn) называется число (х,у)= 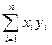
Для любых двух векторов а и b в евклидовом пространстве справедливо неравенство

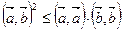
Доказательство:
Возьмем произвольное число t и составим вектор 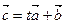
Тогда 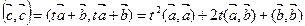
Легко заметить квадратный трехчлен, если 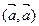 =α,
=α, 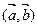 =β, а
=β, а 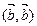 =γ, т.е.
=γ, т.е.
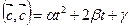
Квадратный трехчлен 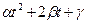 при любом значении t неотрицателен, поскольку
при любом значении t неотрицателен, поскольку 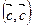 ≥0, следовательно, дискриминант данного трехчлена неположителен.
≥0, следовательно, дискриминант данного трехчлена неположителен.
D= β2- α γ≤ 0, подставим обратно выражения в неравенство:
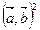 -
- 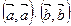 ≤0, или
≤0, или 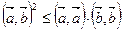 , чтд.
, чтд.
Т.о., нер-во Коши-Буняковского равносильно неравенству 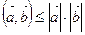
17. Докажите, что для любых векторов  верно неравенство треугольника
верно неравенство треугольника 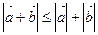 .
.
Для любых двух векторов а и b в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:
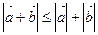
Доказательство:
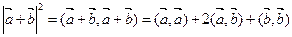
В силу неравенства Коши-Буняковского, согласно которому 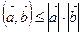 ,
,

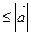 2+2
2+2 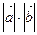 +
+ 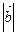 2=(
2=(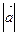 +
+ 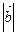 )2
)2
Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны.
Получим: 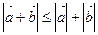
18. Дайте определение ортонормированной системы векторов в 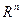 . Приведите пример ортонормированной системы в
. Приведите пример ортонормированной системы в 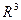 .
.
Если длина вектора равна единице, он называется нормированным вектором: (x, x) = 1, |x| = 1.
Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.
Если векторы системы векторов e 1, e 2, ..., e n попарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (e i, e j) = 0, если i ≠ j, (e i, e i ) = 1.
Если e 1, e 2, ..., e n — ортонормированная система и x = x 1 e1 + x 2 e2 +... + x n e n — разложение вектора x по этой системе, то x i =(x, e i ).
19. Докажите, что ортонормированная система в 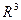 , состоящая из 3 векторов, является базисом пространства
, состоящая из 3 векторов, является базисом пространства 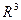 .
.
Если длина вектора равна единице, он называется нормированным вектором: (x, x) = 1, |x| = 1.
Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.
Если векторы системы векторов e 1, e 2, ..., e n попарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (e i, e j) = 0, если i ≠ j, (e i, e i ) = 1.
Если e 1, e 2, ..., e n — ортонормированная система и x = x 1 e1 + x 2 e2 +... + x n e n — разложение вектора x по этой системе, то x i =(x, e i ).
20. Дайте определение ортогонального базиса в 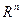 . Приведите пример ортогонального базиса в
. Приведите пример ортогонального базиса в 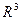 , не содержащего ни одного из векторов стандартного базиса
, не содержащего ни одного из векторов стандартного базиса  ,
, 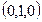 ,
, 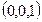 . Ответ обоснуйте.
. Ответ обоснуйте.
Ортогональный (ортонормированный) базис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты. Ортогональный базис — базис, составленный из попарно ортогональных векторов. Этот базис линейнонезависим. Пример ортоганального базиса в R3: v1=(3;0;0), v2=(0;-2;0), v3=(0;0;3).
Матрицы и определители
21. Дайте определение ранга матрицы. Приведите примеры матриц порядка 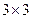 рангов 1, 2 и 3.
рангов 1, 2 и 3.
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
22. Дайте определение произведения матриц  и
и  . Приведите пример, когда
. Приведите пример, когда  определено, а
определено, а 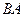 - нет. Существуют ли ненулевые квадратные матрицы
- нет. Существуют ли ненулевые квадратные матрицы  и
и  такие, что
такие, что 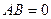 ? Ответ обоснуйте.
? Ответ обоснуйте.
1) Умнож. матр. на число- умножается каждое слогаемое матр. на это число.
2) Умножение на матр. (m*n)*(n*k)=(m*k)=C=A*B. Существует матрица С, каждый эл-т этой матрицы является скалярным произведением соотв.строки матр. А на столбец матр B
Св-ва:
1) (AB)C=A(BC);
2) A(B+C)=AB+AC;
3) q(AB)=(qA)B=A(qB);
4) (AB)t=BtAt; 5) AB НЕ=BA!
23. Укажите, какие из равенств не выполняются для любых матриц 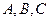 порядка
порядка  : а)
: а) 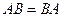 ; б)
; б) 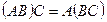 ; в)
; в) 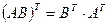 ; г)
; г) 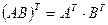 . Приведите примеры, опровергающие неверные равенства.
. Приведите примеры, опровергающие неверные равенства.
24. Укажите, какие из равенств не выполняются для любых обратимых матриц 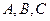 порядка
порядка  и ненулевого числа
и ненулевого числа 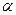 : а)
: а) 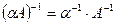 ; б)
; б) 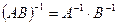 ; в)
; в) 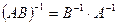 ; г)
; г)  ? Приведите примеры, опровергающие неверные равенства.
? Приведите примеры, опровергающие неверные равенства.
25. Дайте определения вырожденной и невырожденной квадратных матриц порядка 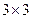 . Приведите примеры таких матриц.
. Приведите примеры таких матриц.
Квадратная матрица А называется невыражденной, если её строки линейно независимы,и вырожденной в противном случае.Св-во: Т.к. элементарные преобразования не меняют ранг матр., то проделав над строками невыражд. матр А элементарн преобразование, получим снова невыражд. матр
26. Сформулируйте основные свойства определителей, связанные с элементарными преобразованиями строк.
1) Если какая либо строка определителя состоит из 0, то и сам определитель равен нулю.
2)При перестановке любых 2-х строк определ.умножается на -1.
3) Определ. с 2 равными строками равен 0.
4) Общий множитель эл-тов любой строки можно вынести за знак определ.
5) Если эл-ты некоторых строк определ. представлены в виде суммы 2-х слагаемых, то и сам определ. равен сумме 2-х определ. 1и2. В определ. 1 указанная строка состоит из первых слагаемых в 2 из вторых.Остальные строки определ. 1и2 те же,что и в начальном.
6) Величина определ. не изменяется, если к одной из строк пребавить другую строку, умноженную на какое угодно число.
7)Сумма произведений эл-тов любой строки на алгебраич. дополнения к соответств. эл-там другой строки равен0.
8) Определю матрицы A равен определителю транспонир. матрицы |A|=|At|.
9)Определитель произведения 2-х матриц равен произведению определ. этих матриц, |A*B|=|A|*|B|.
27. Напишите разложение определителя 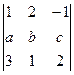 по второй строке.
по второй строке.
28. Проверьте справедливость свойства  для матриц
для матриц  ,
,  .
.
29. Докажите, что 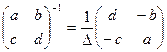 , где
, где  .
.
Доказать, что 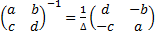 , где
, где 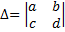 .
.
Докажем, что 
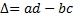
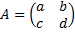
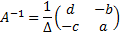

30. Существуют ли матрицы  и
и  такие, что
такие, что 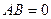 , а
, а 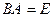 . Ответ обоснуйте.
. Ответ обоснуйте.
Нет (так как во втором случае либо а, либо в равны нулю, а во втором ни а, ни в нулю не равны!)
31. Приведите формулу для вычисления обратной матрицы для матрицы порядка 3. С помощью этой формулы найдите 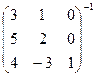 .
.
32. Верно ли, что матричные равенства 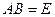 и
и 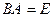 равносильны? Ответ обоснуйте.
равносильны? Ответ обоснуйте.
33. Сформулируйте правило Крамера для решения системы линейных уравнений 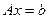 . Докажите правило Крамера для системы линейных уравнений от двух переменных.
. Докажите правило Крамера для системы линейных уравнений от двух переменных.
Пусть дана система АХ = В n линейных уравнений с n неизвестными. Если êAêне равно 0, то система имеет единственное решение:x1=êA1ê/ êA ê; x2=êA2ê/ êA, где Аi, Определители получаются из определителя|А| заменой соответствующего столбца столбцом свобод членов.

В виде матрицы эту систему можно записать таким образом:
A =  , где
, где
ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
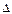 =
=  = 66.
= 66.
Основным определителем является матрица, составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы заменяем каждый столбец коэффициентов при переменной на столбец ответов уравнений.
 1 =
1 = 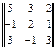 = 43,
= 43,
 2 =
2 =  = 41,
= 41,
 3 =
3 = 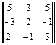 = 51.
= 51.
Затем нужно найти определители 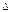 1,
1, 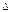 2,
2, 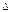 3 и применить правило Крамера. Оно выглядит так:
3 и применить правило Крамера. Оно выглядит так:
x1 =  =
= 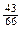 ,
,
x2 = 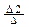 =
= 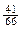 ,
,
x3 = 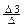 =
=  – для данного случая, а в общем виде оно выглядит следующим образом: xi =
– для данного случая, а в общем виде оно выглядит следующим образом: xi =  .
.
34. Проиллюстрируйте применение правила Крамера для решения системы уравнений 
Комплексные числа
35. Дайте определение и приведите пример комплексно-сопряженных чисел. Докажите, что для комплексных чисел 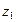 ,
,  справедливы равенства: а)
справедливы равенства: а)  , б)
, б) 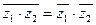 .
.
Комплексное число Z обозначается символом a+ib, где а и в – действительные числа, называемые соответственно действительной частью и мнимой частью комплексного числа; символ i, определяемы условием i*i=-1, называется мнимой единицей. Комплексное число а-ib называется сопряжённым с числом z=a+ib и обозначается z’
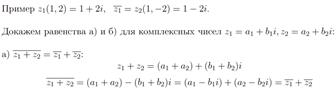
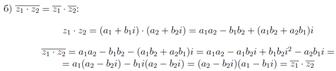
36. Изобразите на плоскости 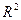 комплексные числа
комплексные числа  ,
,  ,
, 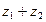 и
и 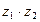 .
.
37. Дайте определение модуля и аргумента комплексного числа 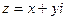 и укажите способ их нахождения.
и укажите способ их нахождения.
Каждому комплексному числу z=a+ib может быть поставлен в соответствие вектор (а,в) принадлежащий R(квадрат). Длина этого вектора, равная корню из сумма а*а и в*в, называется модулем комплексного чтсла z и обозначается через модуль z. Угол «фи» между данным вектором и положительным направлением оси Ox называется аргументом этого числа.
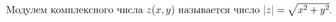

38. Запишите в тригонометрической форме числа 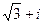 ,
, 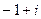 .
.

39. Найдите модуль комплексного числа 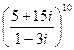
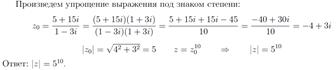
40. Найдите аргумент числа 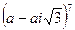 .
.

41. Используя формулу Муавра, вычислите 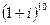 .
.
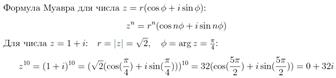
42. Докажите, что корень пятой степени из единицы имеет пять комплексных значений. Как эти значения располагаются на плоскости?


43. Сформулируйте основную теорему алгебры комплексных чисел.
Многочлен n-ой степени имеет на комплексной плоскости ровно n нулей (с учетом их кратности).
Или:
Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
44. Может ли квадратное уравнение в области комплексных чисел: а) не иметь корней; б) иметь более двух корней? Ответ обоснуйте.
а)б) - не верно.
Опираясь на основную теорему алгебры комплексных числел, любое квадратное уравнение(уравнение второй степени) в области комплексных чисел имеет ровно 2 комплексныхкорня (в некоторых случаях комплексные корни могут быть действительными, если они лежат на действительной оси).
45. Решите уравнение в области комплексных чисел: а) 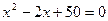 ; б)
; б) 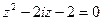 ; в)
; в) 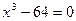 .
.
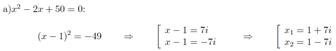
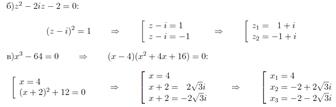
46. Многочлен степени 4 с действительными коэффициентами имеет корень 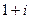 . Докажите, что корнем этого многочлена является число
. Докажите, что корнем этого многочлена является число  .
.

6. Линейные операторы в пространстве 
47. Дайте определение линейного оператора. Проверьте линейность оператора, переводящего вектор 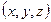 в вектор
в вектор  .
.

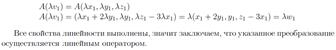
48. Дайте определение матрицы линейного оператора в данном базисе. Приведите пример.
Пусть Ф(е1)=а11е1+а21е2+…+ан1ен; Ф(ен)=а1ен1+а2ен2+…+аннен. Составим матрицу, она и будет называться матрицой линейного оператора.
49. Как изменяется матрица линейного оператора при переходе от одного базиса к другому? Ответ проиллюстрируйте на примере.
Теорема (о переходе к другому базису) Пусть Ae - матрица линейного оператора A
в базисе E = (e1,..., en). Пусть Af - матрица линейного оператора A в базисе F = (f1,..., fn).Тогда матрицы связаны соотношением: 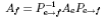 . Где
. Где 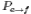 - матрица перехода от базиса E к базису F: F=
- матрица перехода от базиса E к базису F: F= 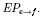
50. Найдите матрицу преобразования 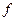 пространства
пространства 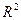 в стандартном базисе: а)
в стандартном базисе: а) 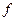 - поворот на угол
- поворот на угол 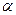 ; б)
; б) 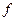 - симметричное отражение векторов относительно прямой
- симметричное отражение векторов относительно прямой 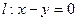 .
.
51. Дайте определение собственных значений и собственных векторов линейного оператора. Приведите пример.
Пусть L — линейное пространство над полем K, — линейное преобразование.
Собственным вектором линейного преобразования A называется такой ненулевой вектор, что для некоторого Ax = λx Собственным значением линейного преобразования A называется такое число, для которого существует собственный вектор, то есть уравнение Ax = λx имеет ненулевое решение.
Упрощённо говоря, собственный вектор - любой ненулевой вектор x, который отображается оператором в коллинеарный λx, а соответствующий скаляр λ называется собственным значением оператора.
52. Как связаны между собой собственные значения линейных операторов 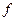 и
и 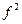 ? Ответ обоснуйте.
? Ответ обоснуйте.
53. Как связаны между собой собственные значения линейных операторов 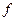 и
и  ? Ответ обоснуйте.
? Ответ обоснуйте.
54. Могут ли все собственные значения ненулевой матрицы быть равными 0? Ответ обоснуйте для квадратных матриц порядка 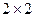 .
.
Составим характеристическое уравнение: 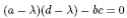 . Мы видим, что при лямбда =0, ad=bc.. Подставим это уравнение в характеристическое и упростим его. Получится:
. Мы видим, что при лямбда =0, ad=bc.. Подставим это уравнение в характеристическое и упростим его. Получится:  . Следователь лямбда = 0, когда 1)ad=bc, 2)a=-d/
. Следователь лямбда = 0, когда 1)ad=bc, 2)a=-d/
55. /
56. Как связаны собственные векторы и собственные значения квадратных матриц 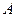 и
и  ? Ответ обоснуйте.
? Ответ обоснуйте.
Пусть v - собственный вектор матрицы A, отвечающий собственному значению лямбда. Тогда 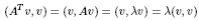 Это означает, что (AT v, v) = лямбда(v, v), а значит AT v = лямбда v. То есть собственные значения исобственные вектора матриц A и AT совпадают.
Это означает, что (AT v, v) = лямбда(v, v), а значит AT v = лямбда v. То есть собственные значения исобственные вектора матриц A и AT совпадают.
57. /
58. Какому алгебраическому уравнению удовлетворяют собственные значения матрицы? Приведите пример.
Собственные значения матрицы A удовлетворяют характеристическому уравнению этой матрицы, то есть det (A - E) = 0.
Пример: матрица 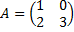
Тогда
det (A -λE) = det

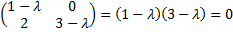
Получаем, что λ = 1, λ = 3 - собственные значения указанной матрицы.
59. /
60. /
61. Дайте определение числа Фробениуса неотрицательной квадратной матрицы. Найдите число Фробениуса для матрицы  : (а)
: (а) 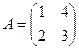 ; (б)
; (б)  . Ответы обоснуйте.
. Ответы обоснуйте.
Числом Фробениуса матрицы A ≥ 0 называется максимальное собственное значение
этой матрицы.
Теорема: Если сумм