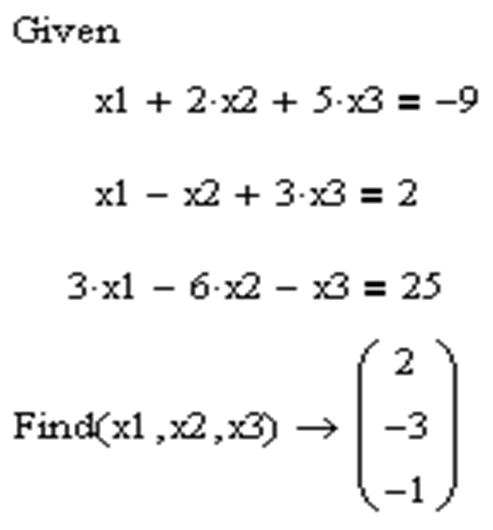Нижняя граница индексации в MathCAD определена системной переменной ORIGIN. По умолчанию ORIGIN=0. Значение переменной можно переопределить. Например, ORIGIN=1.
Векторы и матрицы в MathCAD можно задавать путем ввода их элементов. Для ввода индекса элемента массива используется символ – [.
Поэлементный ввод массива Х
| Вводимые символы | Отображаемые символы |
| X [ 1 Shift+: 5 | X1:=5 |
| X [ 2 Shift+: 8 | X2:= 8 |
| X [ 3 Shift+: 10 | X3:= 10 |
Поэлементный ввод матрицы А
| Вводимые символы | Отображаемые символы |
| A [ 1,1 Shift+: 0.1 | A11 := 0.1 |
| A [ 1,2 Shift+: -2.5 | A12 := -2.5 |
| A [ 2,1 Shift+: -1.0 | A21 := -1.0 |
| A [ 2,2 Shift+: 5.2 | A22 := 5.2 |
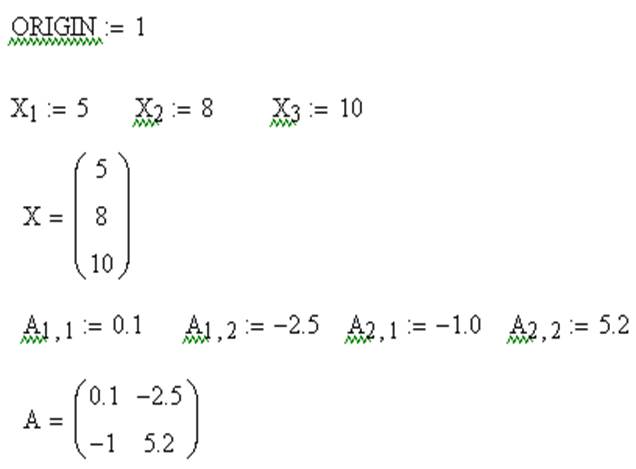
Для операций с матрицами и векторами предназначена панель Matrix, которая открывается щелчком по кнопке 
в панели математических инструментов.
Панель Matrix содержит следующие кнопки:
– определение размеров матрицы;
– ввод элемента массива 
;
– вычисление матрицы, обратной к данной 
;
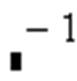– вычисление определителя матрицы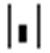 
;
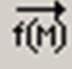– оператор векторизации (поэлементные операции с векторами и матрицами) 
;
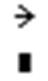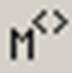– определение столбца матрицы 
;
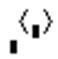– транспонирование матрицы 
;
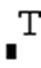– определение ранжированной переменной;
– вычисление скалярного произведения векторов;
– вычисление векторного произведения векторов;
– вычисление суммы компонент вектора.
– визуализация цифровой информации.
Действия, которые необходимо выполнить, чтобы ввести матрицу в рабочий документ при помощи кнопки 
панели Matrix:
1. Ввести с клавиатуры имя матрицы и знак присваивания;
2. Щелчком по кнопке 
открыть окно диалога:
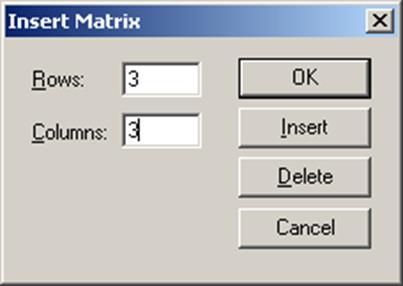
3. Определить число строк (Rows) и число столбцов (Columns) будущей матрицы;
4. Закрыть окно диалога, щелкнув по кнопке OK;
5. Ввести элементы матрицы, установив курсор в поле ввода, которое появится справа от знака присваивания:
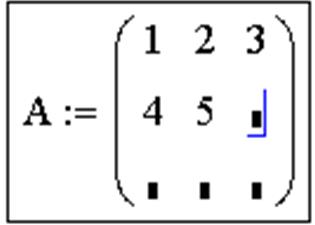
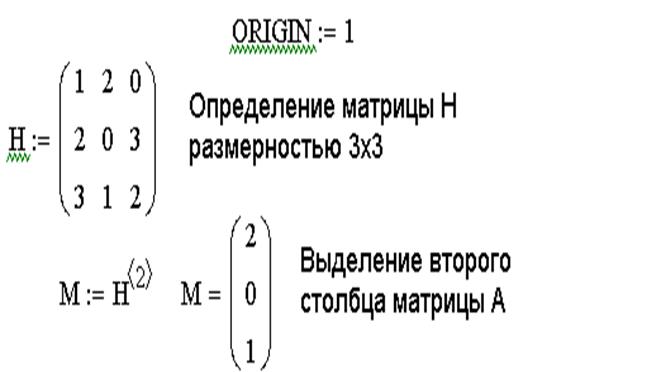
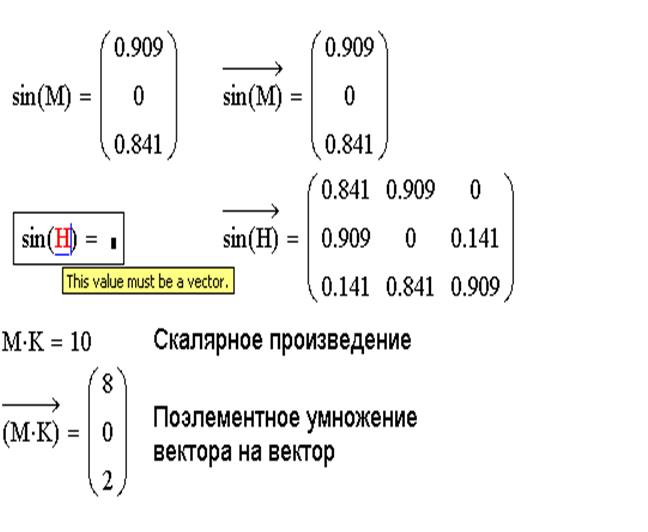
Функции определения матриц и операции с блоками матриц:
matrix(m,n,f) – создает и заполняет матрицу A ={aij} размерности m на n, каждый элемент которой aij равен значению функции f(i,j);
diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
identity(n) – создает единичную матрицу порядка n;
augment(A,B) – из матриц А и В формируется третья матрица, первые столбцы которой содержат матрицу А, а последние - матрицу В (матрицы А и В должны иметь одинаковое число строк);
stack(A,B) – из матриц А и В формируется третья матрица, первые строки которой содержат матрицу А, а последние - матрицу В (матрицы А и В должны иметь одинаковое число столбцов);
submatrix(A,l,k,p,r) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l<k, p<r);
Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами;
Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами;
Функции вычисления различных числовых характеристик матриц:
last(v) – вычисление номера последнего элемента вектора v;
length(v) – вычисление количества элементов вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице (векторе) А;
min(A) – вычисление наименьшего элемента в матрице (векторе) А;
mean(A) – вычисление среднего значения матрицы (вектора) А;
tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;
ranc(A) – вычисление ранга матрицы А;
Функции, реализующие численные алгоритмы:
rref(A) – приведение матрицы А к ступенчатому виду;
geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A = E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;
lsolve(A,b) – решение системы линейных алгебраических уравнений A∙x=b.
lu(A) – выполняет треугольное разложение матрицы А: A = С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;
qr(A) – выполняет разложение матрицы А: A = Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;
cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А = L∙L T, где А - квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;
Функции сортировки:
sort(v) – сортировка элементов вектора v в порядке возрастания их значений;
reverse(v) – перестановка элементов вектора v в обратном порядке;
csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n -й столбец;
rsort(A,n) – перестановка столбцов матрицы А таким образом, чтобы отсортированной оказалась n -я строка.
ЗАДАЧА 1. Сформировать матрицу H из элементов матрицы D, исключив третий столбец и вторую строку.
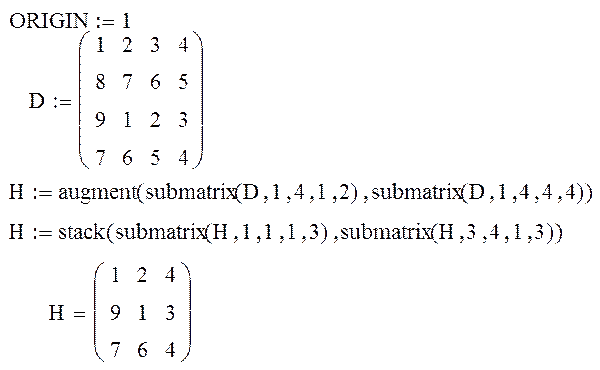
ЗАДАЧА 2. Сформировать матрицу H следующим образом. Первая и последняя строки равны строкам матрицы D, остальные совпадают с матрицей C.
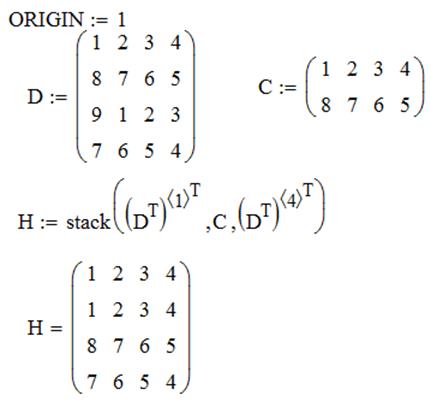
ЗАДАЧА 3. Сформировать матрицу таким образом, чтобы элементы на главной диагонали были равны 1, выше главной диагонали – 2, а ниже – 3.
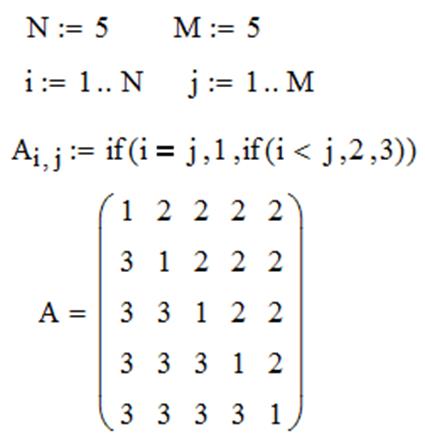
ЗАДАЧА 4. Элементы матрицы формируются по формуле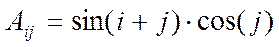 
. Сформировать вектор из максимальных элементов столбцов матрицы А. Найти сумму элементов матрицы, расположенных в четных строках.
ЗАДАЧА 5. Выполнить действия над матрицами А, В, С:
(А Т+ В) С.
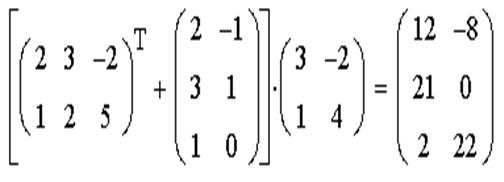
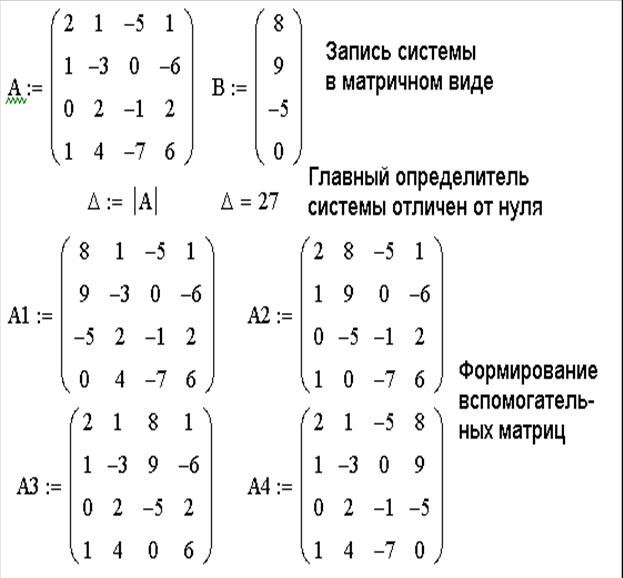
ЗАДАЧА 6. Решить систему линейных уравнений при помощи правила Крамера:
2 x 1+ x 2–5 x 3+ x 4=8,
x 1–3 x 2 –6 x 4=9,
2 x 2– x 3+2 x 4=-5,
x 1+4 x 2–7 x 3+6 x 4=0.
Для решения поставленной задачи необходимо выполнить следующие действия:
1. Сформировать матрицу системы А и вектор правых частей b.
2. Вычислить главный определитель ∆.
3. Сформировать вспомогательные матрицы (удобно скопировать матрицу А несколько раз и последовательно заменять в ней столбцы на вектор b) для вычисления определителей ∆i;
4. Вычислить определители ∆i;
5. Найти решение системы по формуле xi=∆i/∆.
ЗАДАЧА 7. Решить систему линейных уравнений методом обратной матрицы.
Необходимо:
1. Сформировать матрицу коэффициентов и вектор свободных членов системы.
2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов.
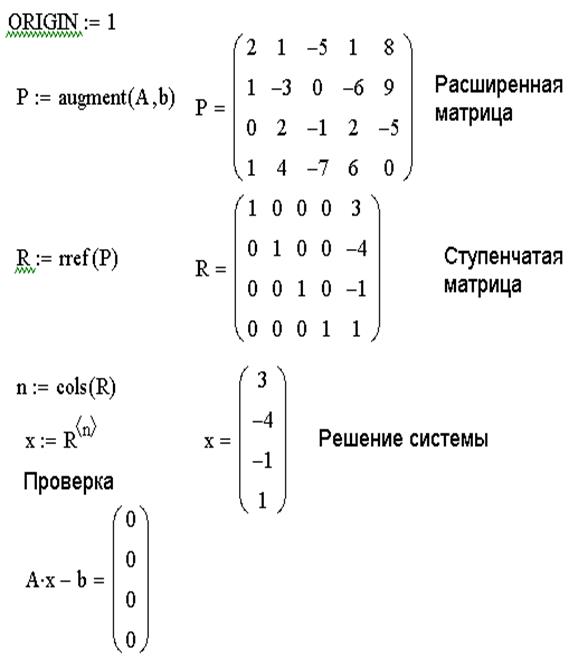
ЗАДАЧА 8. Решить систему линейных уравнений методом Гаусса.
Порядок решения задачи:
1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.
2. Сформировать расширенную матрицу системы при помощи функции augment(A,b);
3. Используя функцию rref(A), привести расширенную матрицу к ступенчатому виду.
4. Получить решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте.
5. Выполнить проверку Ax-B =0.
ЗАДАЧА 9. Решить систему при помощи функции lsolve:
x 1+2 x 2+5 x 3=-9,
x 1– x 2+3 x 3=2,
3x 1–6 x 2– x 3=25.
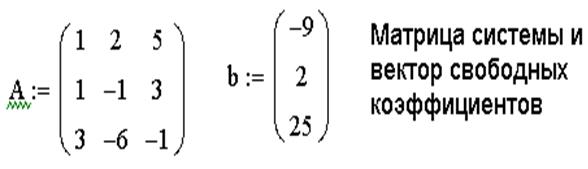
Пример системы, которая не имеет решений:
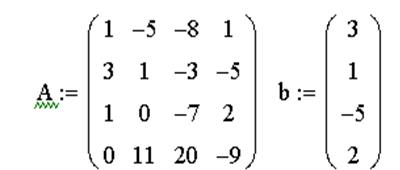
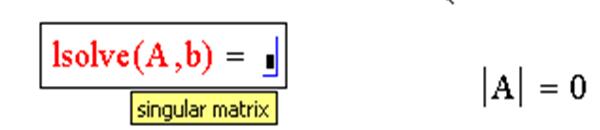
Пример системы, которая имеет бесконечное множество решений
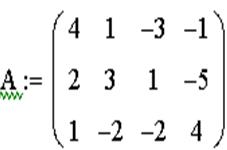
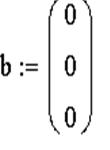
ЗАДАЧА 10. Решить систему при помощи решающего блока.
Решающий блок начинается с ключевого слова Given (Дано), которое необходимо ввести с клавиатуры.
Правее и ниже ключевого слова записываются уравнения системы.
Знак равенства в уравнениях вводится при помощи клавиш Ctrl + = или выбирается на панели инструментов Boolean.
Правее и ниже последнего уравнения системы вводится функция Find(x1,x2,…xn) (Найти), в скобках перечисляются имена переменных, значения которых нужно найти.
Численное решение системы можно получить, поставив знак равенства после функции Find(x1,x2,…xn).
Символьное решение получится, если после функции Find(x1,x2,…xn) указать знак стрелки, который находится в панели инструментов Symbolic (Ctrl + .).
