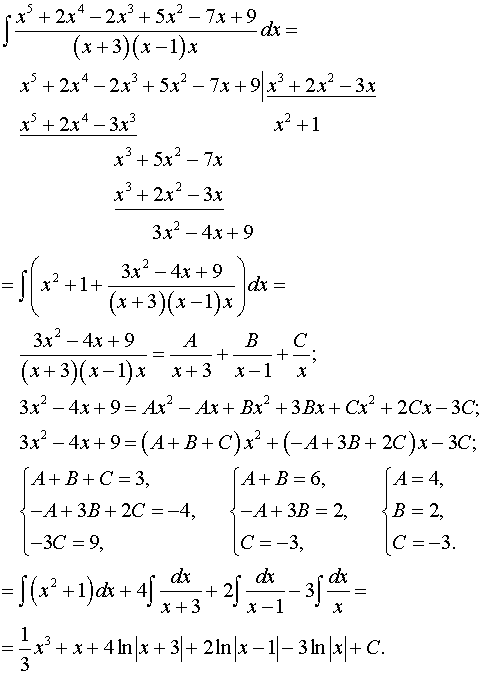Интегралы. Справочный материал
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Свойства.
1.  .
.
2.  .
.
3. 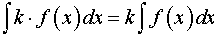 .
.
4.  .
.
Некоторые неопределенные интегралы.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 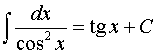 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13. 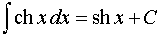 . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19. 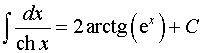 .
.
20.  .
.
21.  .
.
22. 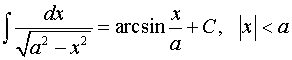 .
.
23.  .
.
24. 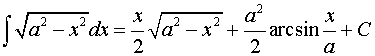 .
.
25. 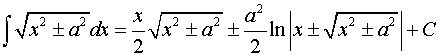
Задача 1
Интегрирование по частям.
Постановка задачи. Найти неопределенный интеграл
 .
.
План решения. Пусть  имеет очевидную первообразную
имеет очевидную первообразную  , а
, а 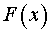 – дифференцируемая функция, причем ее производная
– дифференцируемая функция, причем ее производная  является более простой функцией, чем
является более простой функцией, чем 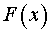 . Тогда применяем формулу интегрирования по частям
. Тогда применяем формулу интегрирования по частям
 .
.
Если метод избран удачно, то интеграл в правой части этого равенства оказывается табличным или известным образом сводится к табличному, например, повторным интегрированием по частям.
Примечание 1. Чаще всего в учебниках и справочных пособиях встречается следующая формула интегрирования по частям (обозначения которой мы и используем в решениях):
 .
.
Примечание 2. В случае определенного интеграла имеем формулу
 .
.
Задача 1. Найти неопределенные интегралы.



Задача 2
Интегрирование по частям.
Постановка задачи. Найти неопределенный интеграл
 .
.
План решения. Пусть  имеет очевидную первообразную
имеет очевидную первообразную  , а
, а 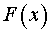 – дифференцируемая функция, причем ее производная
– дифференцируемая функция, причем ее производная  является более простой функцией, чем
является более простой функцией, чем 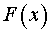 . Тогда применяем формулу интегрирования по частям
. Тогда применяем формулу интегрирования по частям
 .
.
Если метод избран удачно, то интеграл в правой части этого равенства оказывается табличным или известным образом сводится к табличному, например, повторным интегрированием по частям.
Примечание 1. Чаще всего в учебниках и справочных пособиях встречается следующая формула интегрирования по частям (обозначения которой мы и используем в решениях):
 .
.
Примечание 2. В случае определенного интеграла имеем формулу
 .
.
Задача 2. Вычислить определенные интегралы.




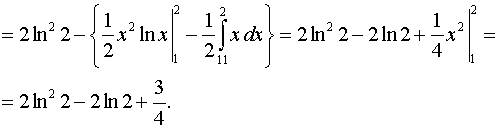
Задача 3
Интегрирование подведением под знак дифференциала.
Постановка задачи. Найти неопределенный интеграл

План решения. Пусть  имеет очевидную первообразную
имеет очевидную первообразную  , а
, а 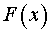 есть функция этой первообразной, т.е.
есть функция этой первообразной, т.е.  . Тогда
. Тогда
 .
.
Такого рода преобразование называется подведением под знак дифференциала.
Если метод избран удачно, то последний интеграл оказывается таблицным или известным образом сводится к табличному.
Задача 3. Найти неопределенные интегралы.

Интегрирование подведением под знак дифференциала.
Постановка задачи. Найти неопределенный интеграл

План решения. Пусть  имеет очевидную первообразную
имеет очевидную первообразную  , а
, а 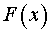 есть функция этой первообразной, т.е.
есть функция этой первообразной, т.е.  . Тогда
. Тогда
 .
.
Такого рода преобразование называется подведением под знак дифференциала.
Если метод избран удачно, то последний интеграл оказывается таблицным или известным образом сводится к табличному.
Примечание. В случае определенного интеграла все аналогично, только необходимо подставить пределы интегрирования.
Интегрирование рациональных функций с простыми вещественными корнями знаменателя.
Постановка задачи. Найти неопределенный интеграл
 .
.
План решения.
1. Введем обозначения:
 ,
,
 .
.
Сравним степени числителя  и знаменателя
и знаменателя  .
.
Если подынтегральная функция – неправильная рациональная дробь, т.е. степень числителя  больше или равна степени знаменателя
больше или равна степени знаменателя  , то сначала выделяем целую часть рациональной функции, поделив числитель на знаменатель:
, то сначала выделяем целую часть рациональной функции, поделив числитель на знаменатель:

Здесь многочлен  – остаток от деления
– остаток от деления  на
на  , причем степень
, причем степень  меньше степени
меньше степени  .
.
2. Разложим правильную рациональную дробь

на элементарные дроби. Если ее знаменатель имеет простые вещественные корни  , т.е.
, т.е.  , то разложение на элементарные дроби имеет вид
, то разложение на элементарные дроби имеет вид
 .
.
3. Для вычисления неопределенных коэффициентов  приводим к общему знаменателю дроби в правой части равенства, после чего приравниваем коэффициенты при одинаковых степенях
приводим к общему знаменателю дроби в правой части равенства, после чего приравниваем коэффициенты при одинаковых степенях  в числителях слева и справа. Получим систему
в числителях слева и справа. Получим систему  уравнений с
уравнений с  неизвестными, которая имеет единственное решение.
неизвестными, которая имеет единственное решение.
4. Интегрируем целую часть (если она есть) и элементарные дроби, используя табличные интегралы, и записываем ответ
 ,
,
где  – многочлен степени
– многочлен степени 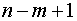 .
.
Задача 4. Найти неопределенные интегралы.