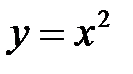Лекция по теме «Обратная функция»
ПОНЯТИЕ ОБРАТИМОЙ ФУНКЦИИ.
ДОСТАТОЧНОЕ УСЛОВИЕ ОБРАТИМОСТИ.
На рисунках приведены две функции, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет (рис.1). Таким образом, функция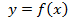 
обладает свойством, не характерным для функции 
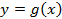: какое бы число 
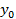из множества значения функции f(x) ни взять, оно является значением функции только в одной точке 
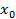. Говорят, что такая функция обратима.
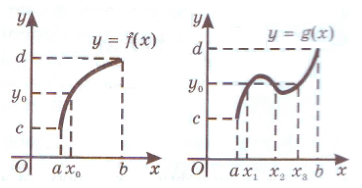
Рис. 1
У функции 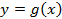значение 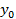можно получить сразу в трех точках 
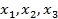. Поэтому такая функция не обратима.
Определение 1. Функцию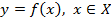 
называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Теорема. Если функция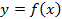 
монотонна на множестве X, то она обратима.
Попробуйте самостоятельно определить, какая из предложенных функций обратима?:
а)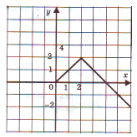 
б)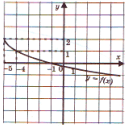 
в) y = 2x + 5;
г) y = -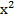 
+ 7.
Ответ:
а) – функция и возрастает и убывает, значит, она немонотонна, поэтому необратима
б) – функция убывает, значит, она монотонна, поэтому обратима
в) – линейная функция, k=2, то есть функция возрастает, значит, она монотонна, поэтому обратима
г) – квадратичная функция, график – парабола, ветви вниз, то есть функция и возрастает и убывает, значит, она немонотонна, поэтому необратима
Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Например, мы можем взять немонотонную функцию и рассмотреть ее только на одном промежутке, где она только возрастает или только убывает, тогда условие обратимости будет выполняться. Например, функция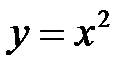 
при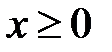 
будет возрастающей функцией, поэтому при таких значениях х она обратима.
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ.
АЛГОРИТМ СОСТАВЛЕНИЯ ОБРАТНОЙ ФУНКЦИИ.
Определение 2. Пусть обратимая функция y=f(x) определена на множестве Х и область ее значений Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции. Эту функцию обозначают x=f -1(y),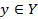 
и называют обратной по отношению к функции y=f(x), 
.
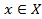Алгоритм составления обратной функции для функции y=f(x),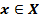 
.
- Убедиться, что функция y=f(x) обратима на промежутке Х.
- Выразить переменную х через у из уравнения y=f(x), учитывая при этом, что .
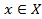- В полученном равенстве поменять местами х и у. Вместо х=f -1(y) пишут y=f -1(x).
Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=2x-5 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение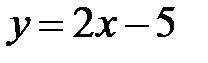 
относительно х;
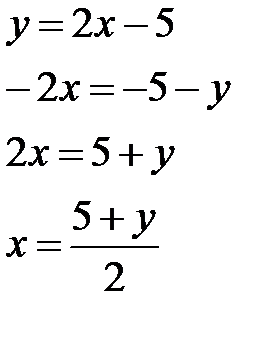
Переобозначим переменные, получим искомую обратную функцию
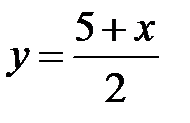Она определена и возрастает на R.
Пример 2. Показать, что для функци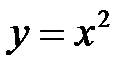и при 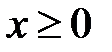существует обратная функция, и найти ее аналитическое выражение.
Решение.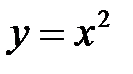 
– квадратичная функция. При 
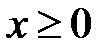функция непрерывна, монотонно возрастает в своей области определения, следовательно, она обратима. Найдем ее:
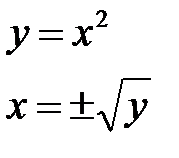
Так как по условию 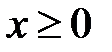, то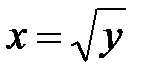 
Переобозначим переменные:
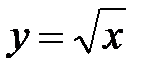– обратная функция для