Интегральные исчисление
1.Первообр.ф-ия и неопр.интегал.Таблица неопр.интегралов и их сво-ва.
Пусть есть ф-ия f(x),опред. на некотором промежутке.Первообразной ф-ией F(x) для f(x) на промеж. Х назыв.ф-ия, производная от которой равняется заданной ф-ии. F’(x)=f(x) Теор. Если F и F1 первообр.для ф-ии f на промежутке Х <=> F(х)-F1(х)=const Док-во: F(х),F1(х) две первообр. Составим их разность 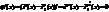
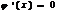 Х <=>
Х <=> 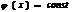
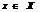 ; F(х)-F1(х)=const,F-перв.=> F1(х)-перв.
; F(х)-F1(х)=const,F-перв.=> F1(х)-перв. 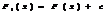
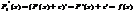 C1(X)-множ-во ф-ий диф-мых на промеж. Х, введем отнош.эквив-сти F1~ F1 <=> F1-F2=c,обладающ. Всеми сво-ми рав-ва F~F, F1~F2=> F2~ F1, F1~F2 и F2~F3 => F1~F3.Неопр интеграл для ф-ии
C1(X)-множ-во ф-ий диф-мых на промеж. Х, введем отнош.эквив-сти F1~ F1 <=> F1-F2=c,обладающ. Всеми сво-ми рав-ва F~F, F1~F2=> F2~ F1, F1~F2 и F2~F3 => F1~F3.Неопр интеграл для ф-ии 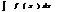
назыв множ-во всех первообр, т е множ-во таких ф-ий 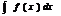 ={F(x)| F(x)’=f(x)}={F(x)+c, c
={F(x)| F(x)’=f(x)}={F(x)+c, c 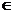 R, F’(x)=f(x)}=F(x)+c Сво-ва: 1)линейности:
R, F’(x)=f(x)}=F(x)+c Сво-ва: 1)линейности: 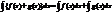 ;
; 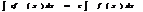 ;
; 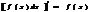 Док-во: вычислим произв от левой части =f(x)+g(x) от правой части =
Док-во: вычислим произв от левой части =f(x)+g(x) от правой части = 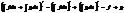
2. Замена переменной в неопр интеграле.Интегрирование по частям
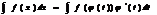
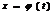 Т ф-ла подведения под знак диф-ла. И справа и слева стоит ф-ия зависящая от t (л.ч.)t’=
Т ф-ла подведения под знак диф-ла. И справа и слева стоит ф-ия зависящая от t (л.ч.)t’= 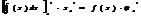 (пр.ч)t’=
(пр.ч)t’= 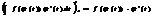 ; (л.ч)’=(пр.ч)’
; (л.ч)’=(пр.ч)’
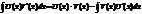 U(x),V(x) ф-ии диф-мые на множ-ве Х Док-во: (U(x)*V(x))’=U’(x)V(x)+V’(x)U(x) л.ч.
U(x),V(x) ф-ии диф-мые на множ-ве Х Док-во: (U(x)*V(x))’=U’(x)V(x)+V’(x)U(x) л.ч. 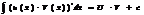 пр.ч.
пр.ч. 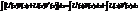
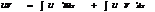

Интегрирование простейших рациональных дробей.
Рац.дробью назыв.отношение двух многочл.Она назы правильной ели степень числит меньше степени знаменателя,в противном случае неправ. 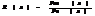
неправ дробь можно представить как сумму многочленов 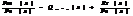 Опред. простейшими рац дробями назыв след рац дроби:1)
Опред. простейшими рац дробями назыв след рац дроби:1) 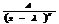 ,R
,R 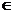 N;
N;
2) 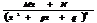 ,
, 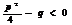
1случай: 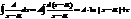 ;
; 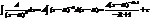 ; пример:
; пример: 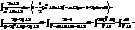
= 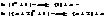
простейшая рац дробь 2 при R=1 может быть проинт-на с помощью замены 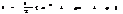
при R>1 существ.п овторяющ-ся процедуры позволяющие вычислять этот интегр.
4.интегрир.рац.дробей путем выделения целой части и разложения правильной дроби на простейшие рац.дроби
Прав.рац дробь может быть представлена как сумма простейших рац.дробей,и такое представление единственно, с точностью до порядка слагаемых. 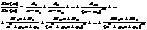
где 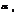 -первый корень многочлена, аналогичные слагаемые записываются для всех веществ. корней где
-первый корень многочлена, аналогичные слагаемые записываются для всех веществ. корней где 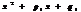 входит в разложение знаменателя степени l1. Если корень имеет кратность 1 его назыв.простым корнем, если >1 то кратным.
входит в разложение знаменателя степени l1. Если корень имеет кратность 1 его назыв.простым корнем, если >1 то кратным.
Инетегрир.тригонометр.выраж. и иррациональн.выраж.
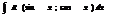
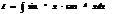 1)
1) 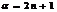
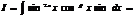
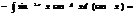
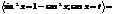
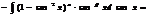
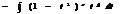 2)
2) 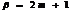
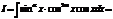
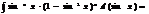
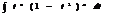
3) 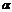 и
и 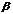 четные числа
четные числа 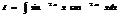
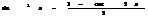 ;
; 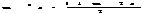
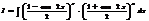
универсальная замена переменной
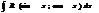
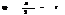
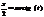
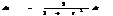
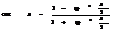
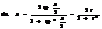
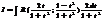
Опред опред интеграла.
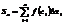 Пусть ф-ия f(x) опред и непрерывна на [а,в].Разобъем этот отрезок на n-частей. Оставим интегр сумму: Sn=f(c1)Dx1+...+f(cn) Dxn
Пусть ф-ия f(x) опред и непрерывна на [а,в].Разобъем этот отрезок на n-частей. Оставим интегр сумму: Sn=f(c1)Dx1+...+f(cn) Dxn
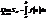 Составим предел интег сумм:
Составим предел интег сумм:
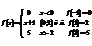 -Опред интеграл- назыв предел интегральных сумм при числе отрезков разбиен ®∞ и стремл длины мах отрезка разбиения к нулю. Ф-ия у=f(x) назыв кусочно непрерывн на отрезке, если она ограничена на нем и имеет конечное число точек разрыва. (Например:
-Опред интеграл- назыв предел интегральных сумм при числе отрезков разбиен ®∞ и стремл длины мах отрезка разбиения к нулю. Ф-ия у=f(x) назыв кусочно непрерывн на отрезке, если она ограничена на нем и имеет конечное число точек разрыва. (Например:
Ф-ия непрерывна на пром при х<0. (0;2) х>2
Теор: Если ф-ия кусочно-непрерывна на [а,в],то она интегрируема на этом отрезке. Следствие1:Непрер ф-ии интегрируемы на конечном промеж. 2: Элемент ф-ии интегр на отрезках их существов.Геометр смысл:1-интегр суммы-площадь ступенчатой фигуры. 2- опред инт-площадь криволин трапец. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и т.д. сводится к вычисл опред инт.
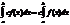 7. Св-ва опред интеграла. 1-Линейность относит. Подынтегральн ф-ии: а)однородность:
7. Св-ва опред интеграла. 1-Линейность относит. Подынтегральн ф-ии: а)однородность:
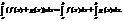 в)адитивность:
в)адитивность:
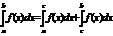 2-адитивность для промежутка интегрирован:
2-адитивность для промежутка интегрирован:
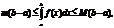
3-если ф-ия такова, что выполняется m£f(x)£M на отрезке [a;b] где M и m – мах и мин Знач ф.
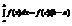 4-(о ср) Если ф-ия f(x) непрерывна на отрезке [a;b], то сущ такая тчк с?[a; b], что
4-(о ср) Если ф-ия f(x) непрерывна на отрезке [a;b], то сущ такая тчк с?[a; b], что
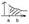 т. е. опред инт от перем ф-ии = произвед знач подынтегр ф-ии в нек-й проме тчк с отр интегр [a; b] и длин b-a эт отр.
т. е. опред инт от перем ф-ии = произвед знач подынтегр ф-ии в нек-й проме тчк с отр интегр [a; b] и длин b-a эт отр.
Производная опред интегр по верх преде.
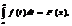 Если f(x) непрер на [a;b], то инт с переем верхним пределом имеет произв в каждой внутрен тчк и ее знач=знач подынтегр ф-ии:
Если f(x) непрер на [a;b], то инт с переем верхним пределом имеет произв в каждой внутрен тчк и ее знач=знач подынтегр ф-ии:
 |
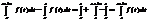 Док-во:
Док-во:
Сост приращение ф-ии: DF=F(x+Dx)-F(x)=
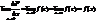
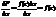
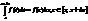
По т/ о среднем:
Dx -люб знака
Инте=длине пром, Произв:
, f(x) - непрер
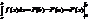 Ф-ла Н-Л. Если f(x)-непрер на [a;b], а F(x)-нек первообразн, то
Ф-ла Н-Л. Если f(x)-непрер на [a;b], а F(x)-нек первообразн, то

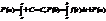
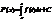 Док-во: Пусть F(x)-нек первообр, она отлич от другой первообр константой:
Док-во: Пусть F(x)-нек первообр, она отлич от другой первообр константой: