Формулировка второго закона Кирхгофа.

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках , где n – число источников ЭДС в контуре;
m – число элементов с сопротивлением в контуре;
– напряжение или падение напряжения на k -ом элементе контура.

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Таким образом, второй закон Кирхгофа позволяет выписать интегро-дифференциальное уравнение для силы тока :

,

здесь 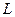- индуктивность катушки, - суммарное сопротивление, - ёмкость конденсатора, 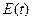- суммарное напряжение на конденсаторе в момент времени ().

Для того чтобы найти выражения переходных токов, целесообразно перейти к изображению интегро-дифференциального уравнения Кирхгофа, то есть построить соответствующее операторное уравнение. Для осуществления данного перехода необходимо найти начальные условия , учитывая условия конкретной задачи. После чего, с помощью элементарных алгебраических преобразований выразим изображение переходного тока . Последний этап решения задач рассматриваемого вида сводится к отысканию оригинала для найденного изображения переходного тока.

Сила тока удовлетворяет уравнению , найти , если , , , , , .

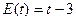Дифференциальное уравнение Кирхгофа для этой задачи имеет вид:

.

Решим это уравнение операторным методом. Будем полагать, что 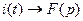. Образом уравнения является следующее равенство:

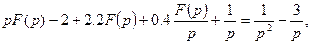
Найдем оригинал получившегося изображения, разложив дроби на простые слагаемые методом неопределенных коэффициентов. Представим наше изображение в виде суммы трех изображений:

Приведем данное выражение к общему знаменателю и приравняв числители в двух представлениях одного и того же изображения получим равенство:

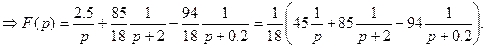
Таким образом, мы отыскали изображение тока, для того чтобы довести задачу до ответа необходимо найти оригинал этого изображения. Оригиналом получившейся разности, в силу линейности преобразования Лапласа, будет сумма трех оригиналов слагаемых, следовательно, .

Заметим, что часто встречающейся является ошибка неверного определения изображений функций, находящихся в правой части уравнения Кирхгофа, так что на этот момент решения следует обратить серьёзное внимание.

Контур подключен к постоянной э.д.с. (см. рис.) При установившемся режиме включается рубильник и накоротко замыкает сопротивление . Найти выражение переходного тока. .

Дифференциальное уравнение Кирхгофа до включения рубильника в данном случае имеет вид:

Согласно постановке задачи . Решим это уравнение операционным методом, предполагая, что .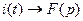

.

Найдем оригинал получившегося изображения, разложив дроби на простые слагаемые методом неопределенных коэффициентов:

Таким образом, .

Установившийся ток в контуре до включения рубильника есть 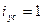. Дифференциальное уравнение Кирхгофа после замыкания рубильника имеет вид:

.

Решим это уравнение операционным методом.

.

Как и в предыдущем случае воспользуемся методом неопределенных коэффициентов для разложения изображения на слагаемые.

Оригиналом получившейся разности, как нетрудно заметить, будет .

Ниже приведены варианты контрольной работы.

Вариант 1

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

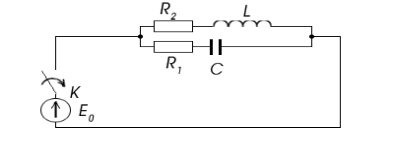
4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений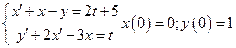

8. Решить интегральное уравнение

9. В контур (см. рис.) при нулевых начальных условиях подключена э.д.с. . Найти выражение переходного тока при при условиях колебательного процесса.

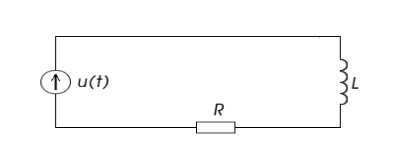
10. Найти изображение функции заданной следующим графиком:

 

Вариант 2

1. Является ли оригиналом функция ?
2. Найти изображения оригинала:
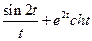
3. Найти оригиналы, соответствующие изображению:
4. Не вычисляя интегралы, найти изображение
5. Вычислить интеграл
6. Найти решение задачи Коши
7. Решить систему уравнений
8. Решить интегральное уравнение
9. На рисунке изображена цепь, замыкаемая и размыкаемая рубильником . Рубильник остается замкнутым в течение 2 секунд и разомкнутым в течение секунд, причем эта операция повторяется периодически в той же последовательности. Определить выражения тока в цепи при третьем замыкании и третьем размыкании, предполагая, что .

10. Найти изображение периодической функции заданной следующим графиком:

Вариант 3

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. Контур подключен к постоянной э.д.с. (см. рис.) При установившемся режиме включается рубильник и накоротко замыкает сопротивление . Найти выражение переходного тока.

10. Найти изображение функции заданной следующим графиком:

 

 

Вариант 4

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) действует синусоидальное напряжение . В момент рубильник замыкает накоротко цепь . Найти выражения переходных токов.

 

10. Найти изображение периодической функции заданной следующим графиком:

 

Вариант 5

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 6

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл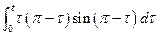

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. Найти условия существования колебательного процесса при подключении контура (см. рис.) к постоянной э.д.с. .

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 7

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение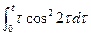

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

 

10. Найти изображение функции заданной следующим графиком:

 

 

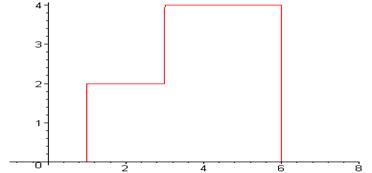
Вариант 8

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение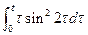

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений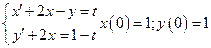

8. Решить интегральное уравнение

9. На рисунке изображена цепь, замыкаемая и размыкаемая рубильником . Рубильник остается замкнутым в течение секунд и разомкнутым в течение 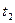секунд, причем эта операция повторяется периодически в той же последовательности. Определить выражения тока в цепи при втором замыкании и втором размыкании, предполагая, что .

10. Найти изображение периодической функции заданной следующим графиком:

 

 

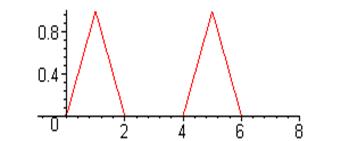
Вариант 9

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В контур (см. рис.) при нулевых начальных условиях подключена э.д.с. . Найти выражение переходного тока при при условиях колебательного процесса.

 

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 10

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В контур (см. рис.) подключена периодическая э.д.с. с периодом : . При каком начальном условии в контуре возникает периодический ток, вызванный действием заданной э.д.с.?

 

10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 11

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению: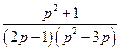

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

 

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 12

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл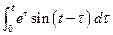

6. Найти решение задачи Коши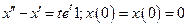

7. Решить систему уравнений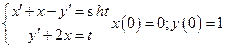

8. Решить интегральное уравнение

9. На рисунке изображена цепь, замыкаемая и размыкаемая рубильником . Рубильник остается замкнутым в течение 2 секунд и разомкнутым в течение секунд, причем эта операция повторяется периодически в той же последовательности. Определить выражения тока в цепи при втором замыкании и втором размыкании, предполагая, что .

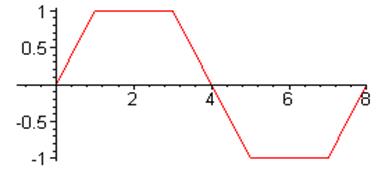
10. Найти изображение функции заданной следующим графиком:

 

 

Вариант 13

1. Является ли оригиналом функция ?

2. Найти изображения оригинала: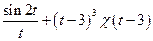

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В контур (см. рис.) подключена периодическая э.д.с. с периодом : . При каком начальном условии в контуре возникает периодический ток, вызванный действием заданной э.д.с.

10. Найти изображение функции заданной следующим графиком:

 

 

Вариант 14

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В контур (см. рис.) при нулевых начальных условиях подключена э.д.с. 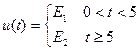. Найти выражение переходного тока при при условиях колебательного процесса.

 

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 15

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

 

10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 16

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

 

10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 17

1. Является ли оригиналом функция ?

2. Найти изображения оригинала: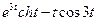

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. Контур подключен к постоянной э.д.с. (см. рис.) При установившемся режиме включается рубильник и накоротко замыкает сопротивление . Найти выражение переходного тока. .

 

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 18

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение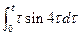

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. В схеме (см. рис.) действует синусоидальное напряжение . В момент рубильник замыкает накоротко цепь . Найти выражения переходных токов.

 

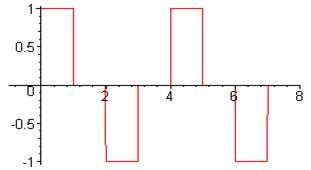
10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 19

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений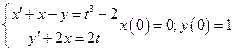

8. Решить интегральное уравнение

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

10. Найти изображение периодической функции заданной следующим графиком:

 

 

 

Вариант 20

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений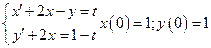

8. Решить интегральное уравнение

9. Найти условия существования колебательного процесса при подключении контура (см. рис.) к постоянной э.д.с. .

 

10. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 21

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение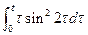

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение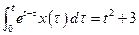

9. В схеме (см. рис.) при включенном рубильнике напряжение на конденсаторе равно , а ток через катушку индуктивности равен . При выключенном рубильнике начинается разряд конденсатора. В конденсаторе предполагается наличие апериодических разрядов. Найти напряжение на конденсаторе в момент времени .

10. Найти изображение функции заданной следующим графиком:

 

 

Вариант 22

1. Является ли оригиналом функция ?

2. Найти изображения оригинала:

3. Найти оригиналы, соответствующие изображению:

4. Не вычисляя интегралы, найти изображение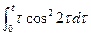

5. Вычислить интеграл

6. Найти решение задачи Коши

7. Решить систему уравнений

8. Решить интегральное уравнение

9. На рисунке изображена цепь, замыкаемая и размыкаемая рубильником . Рубильник остается замкнутым в течение секунд и разомкнутым в течение 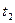секунд, причем эта операция повторяется периодически в той же последовательности. Определить выражения тока в цепи при втором замыкании и втором размыкании, предполагая, что .

10. Найти изображение периодической функции заданной следующим графиком:

 

 

Вариант 23

11. Является ли оригиналом функция ?

12. Найти изображения оригинала:

13. Найти оригиналы, соответствующие изображению:

14. Не вычисляя интегралы, найти изображение

15. Вычислить интеграл

16. Найти решение задачи Коши

17. Решить систему уравнений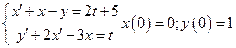

18. Решить интегральное уравнение

19. В контур (см. рис.) при нулевых начальных условиях подключена э.д.с. . Найти выражение переходного тока при при условиях колебательного процесса.

20. Найти изображение функции заданной следующим графиком:

 

 

 

Вариант 24

1. Найти изображ