НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ: ИХ ВЫЧИСЛЕНИЕ И ИССЛЕДОВАНИЕ НА СХОДИМОСТЬ
Повторение: замечательные пределы
Для освоения материала нужно помнить пять замечательных пределов (в терминологии замены на эквивалентные):
1. 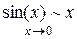 Следствия:
Следствия: 


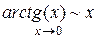
2......
3. 
 . Следствие:
. Следствие: 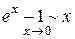
4. 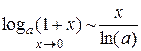
 Следствие:
Следствие: 
5. 
 Следствие:
Следствие: 
Вместо аргумента (икса) в замечательных пределах может также выступать функция, стремящаяся к нулю в искомой точке.
Например можно сказать, что  или
или  . Однако если мы напишем
. Однако если мы напишем  то это будет неверно, поскольку аргумент здесь к нулю не стремится.
то это будет неверно, поскольку аргумент здесь к нулю не стремится.
Два типа несобственных интегралов
Несобственный интеграл первого типа имеет бесконечность в качестве одного или обоих пределов интегрирования б:
 ,
, 

Несобственный интеграл второго типа похож на обычный определённый интеграл, но отличается от него тем, что значение подынтегральной функции  в одном или в обоих концах промежутка интегрирования является бесконечным:
в одном или в обоих концах промежутка интегрирования является бесконечным:
 ,
, 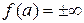 и/или
и/или 
Пример несобственного интеграла первого типа: 
Пример несобственного интеграла второго типа: 
(он несобственный, т.к. значение подынтегральной функции в нуле бесконечно)
Как вычисляются несобственные интегралы?
Несобственные интегралы, которые существуют и имеют конечное значение, называются сходящимися, остальные – расходящимися. Вычисляются данные интегралы по уже знакомой нам теореме Ньютона-Лейбница, с той разницей, что мы не подставляем бесконечность в первообразную в буквальном смысле, а берём предел в ней.
Теорема Ньютона-Лейбница: 
Примеры вычисления несобственных интегралов, которые являются сходящимися:

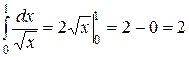
Если нам «не повезло», и в ответе получается бесконечное значение, то интеграл будет расходящимся. Пример:

Задачи для самостоятельного решения.
Вычислить или установить расходимость:
2.1  2.2
2.2 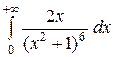 2.3
2.3 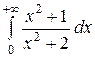 2.4
2.4 
2.5 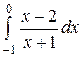
Исследование несобственных интегралов на сходимость.
Весьма часто возникает необходимость, не вычисляя значения самого несобственного интеграла, понять, сходится он или расходится. Для этого мы можем заменить его на другой, более простой, который не равен исходному, но сходится или расходится одновременно с исходным, т.е. в этом отношении «равносилен» ему. Для таких «расносильных» интегралов, в отличие от равенства, мы будем использовать значок  .
.
Утверждение 1: если функции  имеют постоянный знак на некотором луче
имеют постоянный знак на некотором луче  и функции
и функции  эквивалентны при
эквивалентны при  , то несобственные интегралы первого типа
, то несобственные интегралы первого типа  и
и  сходятся или расходятся на бесконечности одновременно.
сходятся или расходятся на бесконечности одновременно.
Утверждение 2: если функции  имеют постоянный знак на некотором промежутке
имеют постоянный знак на некотором промежутке 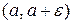 (ε>0 – малый параметр) и функции
(ε>0 – малый параметр) и функции  эквивалентны при
эквивалентны при  , то несобственные интегралы второго типа
, то несобственные интегралы второго типа 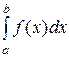 и
и 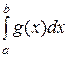 сходятся или расходятся в точке a одновременно.
сходятся или расходятся в точке a одновременно.
Аналогично, если если функции  имеют постоянный знак на некотором промежутке
имеют постоянный знак на некотором промежутке 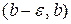 (ε>0 – малый параметр) и функции
(ε>0 – малый параметр) и функции  эквивалентны при
эквивалентны при  , то несобственные интегралы второго типа
, то несобственные интегралы второго типа 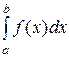 и
и 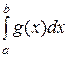 сходятся или расходятся в точке b одновременно.
сходятся или расходятся в точке b одновременно.
Итак, «равносильные» интегралы – это те, подынтегральные функции которых эквивалентны, и таким образом, сходящиеся или расходящиеся одновременно.
4. «Эталонные» интегралы (!)
В качестве «эталонных» интегралов, к которым мы будем сводить остальные, будут использоваться «интегралы с показателем p».
Для интегралов первого типа:  - он расходится при
- он расходится при  и сходится при
и сходится при 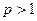
Для интегралов второго типа:  - он сходится при
- он сходится при  и расходится при
и расходится при 
Данные утверждения легко проверить, непосредственно взяв первообразную от степенной функции под интегралом и подставив концы промежутка интегрирования.