Изображение пространственных фигур в параллельной проекции
При изображении пространственных фигур в параллельной проекции применяют теорему Польке-Шварца[9]. Всякий полный невыраженный четырехугольник АВСD вместе с его диагоналями можно рассматривать как изображение тетраэдра любой наперед заданной формы (рис. 10).
Используя теорему Польке-Шварца и свойство параллельного проецирования, я показываю, что изображением призмы и пирамиды (рис. 11), цилиндра и конуса (рис. 12) являются фигуры. [4]
Методы построения сечений многогранников
2.1. Метод следов
Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры F. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры F. Для тех, кто знаком с гомологией[10], удобно ее применять при нахождении образов точек нижнего основания фигуры F - изображения фигуры F. Последовательно соединяя образы этих точек, получим изображение искомого сечения. В дальнейшем будем допускать вольность речи, и говорить «строим сечение» вместо «строим изображение сечения». [5]
Пусть М, N, К - точки секущей плоскости, М1, N1, К1 - их проекции на плоскость основания. При этом для призм и цилиндров ММ1 || NN1, NN1 || КК1, для конусов и
пирамид ММ1∩ NN1∩ КК1 = S (S- вершина). Удобнее обозначать вершины нижнего основания через А1, В1, С1,... верхнего основания - А, В, С,.... Кратко суть метода следов можно записать следующим образом.
1. МN∩ М1N1=X
2. МК∩ М1К1=У
3. ХУ= S - след секущей плоскости
4. A1M1 ∩ S = A0 возможно
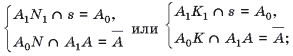
5. АоМ ∩ А1А == А
6. Пункты 4-5 повторить для вершин В1, С1,... нижнего основания фигуры F;
7. 
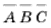- искомое сечение.
Фактически 
где f гомология, заданная осью s и парой точек М1 → М или N1 → N, или К1 → К.
Строить сечение фигуры F секущей плоскостью α методом следов удобно в тех случаях, когда секущая плоскость задана тремя точками, ей принадлежащими, или прямой и не принадлежащей ей точкой, или двумя пересекающимися прямыми, или двумя параллельными прямыми. Во всех случаях легко взять три точки М, N, К, принадлежащие плоскости α, и решение проводить по указанной схеме.
Пример 1. Построим сечение призмы А1B1C1D1ABCD плоскостью, проходящей через три точки М, N, К. Я рассматриваю все случаи расположения точек М, N, К на поверхности призмы (рис. 13).
Рассмотрим случай: М? ВВ1, N? СС1D1D, K? АА1E1. В данном случае, очевидно, что
М1=В1.
Построение.
1.МN ∩ М1К1 = Х
1. МК ∩ М1К1 = У
2. ХУ= S - след секущей плоскости
3. А1К1 ∩ S =Ао
4. АоК ∩ А1А= A, АоК ∩ ЕЕ1= Е.
5. D1N1 ∩ S= Dо
6. DоN ∩ DD1 = D, DоN∩ CC1= C
7. 
- искомое сечение. [7]
Пример 2.
Построим сечение пирамиды SABCDE плоскостью, проходящей через точку М? SBC и прямую l лежащую в грани SED. (рис. 14).
Построение.
1. SМ ∩ ВС=М1
2. М Е ∩МЕ = X, l ∩ЕО = У, ХУ = S - след секущей плоскости
3. S ∩АВ=К, S ∩АЕ = N.
4. ВС ∩ S = Во, ВоМ ∩S B = B, ВоМ ∩ SC = С.
5. 
- искомое сечение.
При объяснении шагов построения можно использовать понятие гомологии или факты стереометрии, опираясь на наглядное представление о данных в условии задачи фигурах. Например, в последнем примере комментарии могут быть следующими.
1. То, что дано, считается построенным.
2. Так как точка М лежит в грани SВС, то прямые SМ и ВС пересекаются, следовательно, легко построить их точку пересечения М1.
3. Прямая l лежит в грани SЕD, значит, она пересекает ребра SD и SE в точках и D и Е.
4. Находим прямую s пересечения плоскости основания и секущей плоскости, используя известные точки М, D, Е в секущей плоскости.
5. Очевиден шаг построения.
6. Прямые ВС и s лежат в одной плоскости, Во - их точка пересечения лежит в секущей плоскости, в плоскости основания и в плоскости SВС. Точка М лежит в секущей плоскости и в плоскости SВС. Следовательно, прямая ВоМ является прямой пересечения секущей плоскости с плоскостью граниSВС. Таким образом, легко построить точки и В и С.
ЗАКЛЮЧЕНИЕ
В задачах на построение сечений не принято проводить исследования, хотя было бы очень полезно его провести. Например, в примере 2 на втором шаге построения рассмотреть случай, когда l || SВ или l || SЕ, на третьем шаге - l || ЕD, на четвертом - s не пересекает АЕ и АВ, на пятом - s || ВС. Рассматривая различные точки, получим при одном условии задачи несколько вариантов решения. В общем случае количество вершин многоугольника сечения может изменяться от 3 до п + 1 - для пирамиды, п +2 - для призмы.
Проведя исследование построения сечения методом следов, я установила, что метод следов легко объясним, нагляден, но не всегда удобен в практике построения сечений многогранников, так как расположение точек Х и У следа s может быть за рамками чертежа, прямые, определяющие точку Х (или Y) могут быть параллельны (рис. 15). В тех случаях, когда применение метода следа затруднено, применяют метод внутреннего проецирования или так называемый метод вспомогательных сечений. [6] Изучив параллельное проецирование, я научилась легко и быстро производить различные построения на плоскости. Эти навыки и умения помогли мне при изучении предметов школьного курса, таких как геометрия и черчение, а также при прохождении учебы на художественном отделении Динской школы искусств.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Геометрия 10-11 класс - А.И. Александров, 1999. с.47
2. Геометрия 10-11 класс - Л.С. Атанасян. «Просвещение», 2001. с.60
3. Модели многогранников - М. Веннинджер. «Мир», М. - 1974. с. 11
4. Начертательная геометрия - А.В. Бубенков, М.Я. Громов, М. - 2000. с.220
5. Начертательная геометрия- С. А. Фролов. «Просвещение», 1999. с. 137
6. Сборник задач по аналитической геометрии и линейной алгебре - А.А. Беклемшнева. М., «Наука», 1987. с.314, с.216
7. Сборник задач по геометрии - В.Т. Базылев, К.И. Дуничев. М. «Просвещение», 1980. с.107
[1] Евклидово пространство – пространство, свойства которого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. называется n -мepное векторное пространство, в котором возможно ввести некоторые специальные координаты (декартовы).
[2] Ортогональная – прямоугольная (Начертательная геометрия А.В. Бубенков)
[3] Свойства в данном преобразовании называют проективными, или инваририантными.
[4] «Геометрия 10-11кл.» Александрова, 1992г.
[5] Эллипс представляет собой геометрическое место точек, сумма расстояний от каяадой из которых до двух данных точек (фокусов) есть величина постоянная.
[6] Аффинные преобразования, точечные взаимно однозначные отображения плоскости (пространства) на себя, при которых прямые переходят в прямые. Если на плоскости задана декартова система координат, то любое А. п. этой плоскости может быть определено посредством т. н. невырожденного линейного преобразования координат х и у точек этой плоскости
[7] Диаметры эллипса - отрезки прямых, проходящих через центр эллипса. Два таких диаметра, каждый из которых делит пополам хорды, параллельные другому, называются сопряженными.
[8] Многогранники - замкнутые пространственные фигуры, ограниченные плоскими многоугольниками.
[9] Польке теорема, основная теорема аксонометрии; впервые была сформулирована немецким геометром К. Польке в 1860 (без доказательства). П. т. утверждает, что три отрезка произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами, представляют собой параллельную проекцию трёх равных и взаимно перпендикулярных отрезков, выходящих из одной точки в пространстве. На основании П. т. три произвольных отрезка, выходящих из одной точки на плоскости проекций, можно принять за изображение координатного трёхосника с одинаковыми масштабными отрезками на его осях. П. т. была обобщена немецким математиком Г. Шварцем, который дал её элементарное доказательство (1864).
[10] Гомология - в проективной геометрии взаимно однозначное преобразование проективной плоскости в себя, при котором сохраняется прямолинейное расположение точек, и остаются неподвижными все точки некоторой прямой (оси Г.).