Тема: «Углы и расстояние в пространстве ».
План
1. Скрещивающиеся прямые. Теоремы о скрещивающихся прямых.
2. Углы с сонаправленными сторонами.
3. Угол между прямыми.
4. Решение задач.
Скрещивающиеся прямые.
Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Две прямые, имеющие лишь одну общую точку, называются пересекающимися.
Итак, возможны три случая взаимного расположения двух прямых в пространстве:
1) прямые пересекаются, т.е. имеют только одну общую точку;
2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;
3) прямые скрещиваются, т.е. не лежат в одной плоскости.
Теорема 1 ( выражает признак скрещивающихся прямых ). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Дано:
AB⊂α, CD 
α=C, C ∉ AB
Доказать: AB скрещивается с DC
Доказательство.
Доказательство будем вести методом от противного.
Допустим, АВ и CD лежат в некоторой плоскости β.
Тогда плоскость β проходит через прямую AB и точку C.
Через прямую AB и не лежащую на ней точку C можно провести плоскость, и притом только одну (следствие из аксиом).Следовательно, β≡α.
Но это невозможно, т.к. прямая CD пересекает α. Пришли к противоречию, ⇒ AB и CD лежат в разных плоскостях (скрещиваются). Теорема доказана.
Теорема 2. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Дано: АВ и CD – скрещивающиеся прямые.
|
|
Доказать: ∃ α: AB ⊂α, CD∥α
Доказательство.
Докажем существование.
1) Проведем AE ∥ CD.
2) Проведем плоскость α через пересекающиеся прямые AE и CD.
3) CD ∥ AE, AE ⊂ α ⇒ CD ∥ α.
Плоскость α - искомая плоскость.
Докажем единственность.
Любая другая плоскость будет пересекать AB, а значит и параллельную ей прямую CD. Поэтому α – единственная. Теорема доказана
2. Углы с сонаправленными сторонами.
Определение сонаправленных лучей.
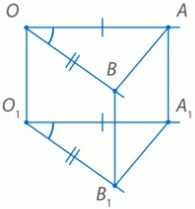
Любая прямая, например ОО1, рассекает плоскость на две
полуплоскости. Если лучи ОА и О1А1 параллельны и лежат
в одной полуплоскости, то они называются сонаправленными.
Лучи О2А2 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.
Теорема о равенстве углов с сонаправленными сторонами.Если стороны двух углов соответственно сонаправлены, то такие углы равны.
Доказательство.
Пусть нам даны параллельные лучи ОА и О1А1 и параллельные
лучи ОВ и О1В1. То есть, мы имеем два угла АОВ и А1О1В1, чьи
стороны лежат на сонаправленных лучах. Докажем, что эти
углы равны.
На стороне луча ОА и О1А1 выберем точки А и А1 так, чтобы отрезки ОА и О1А1 были равны. Аналогично, точки В и В1 выберем так, чтобы отрезки ОВ и О1В1 были равны. Рассмотрим четырехугольник А1О1 ОА. В этом четырехугольнике стороны ОА и О1А1 параллельны и равны. По признаку параллелограмма, четырехугольник А1О1 ОА является параллелограммом. Так как А1О1 ОА – параллелограмм, то стороны О О1 и А А1 параллельны и равны.
Рассмотрим четырехугольник В1О1 ОВ. В этом четырехугольнике
|
|
стороны ОВ и О1В1 параллельны и равны. По признаку
параллелограмма, четырехугольник В1О1 ОВ является
параллелограммом. Так как В1О1 ОВ – параллелограмм, то
стороны ОО1 и В В1 параллельны и равны.
И прямая А А1 параллельна прямой О О1 , и прямая В В1
параллельна прямой О О1, значит прямые А А1 и В В1 параллельны.
Рассмотрим четырехугольник В1А1 АВ. В этом четырехугольнике стороны А А1 и В В1 параллельны и равны. По признаку параллелограмма, четырехугольник В1А1 АВ является параллелограммом. Так как В1А1 АВ – параллелограмм, то стороны АВ и А1В1 параллельны и равны.
Рассмотрим треугольники АОВ и А1О1В1. Стороны ОА и О1А1 равны по построению. Стороны ОВ и О1В1 также равны по построению. А как мы доказали, и стороны АВ и А1В1 тоже равны. Значит, треугольники АОВ и А1О1В1 равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А1О1В1 равны, что и требовалось доказать.
Угол между прямыми.
6.1 Угол между пересекающимися прямыми.
Если прямые пересекающиеся, то мы имеем четыре разных угла.
Углом между двумя прямыми, называется наименьший
из углов между двумя прямыми.
Угол между пересекающимися прямыми а и b обозначим α. Угол α такой, что 
.
6.2 Угол между скрещивающимися прямыми.
Пусть прямые а и b скрещивающиеся. Выберем произвольную точку О. Через точку О проведем прямую 
, параллельную прямой а, и прямую 
, параллельную прямой b. Прямые и 
пересекаются в точке О. Угол между двумя пересекающимися прямыми 
и , угол φ, и называется углом между скрещивающимися прямыми.
|
|
Зависит ли величина угла от выбранной точки О? Выберем точку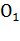 
. Через точку 
проведем прямую 
, параллельную прямой а, и прямую 
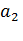, параллельную прямой b. Угол между пересекающимися прямыми 
и обозначим φ1. Тогда углы φ и φ1 - углы с сонаправленными сторонами. Как мы доказали, такие углы равны между собой. Значит, величина угла между скрещивающимися прямыми не зависит от выбора точки О.
Решение задач.
Задача 1. Точка D не лежит в плоскости треугольника ABC, точки M, N, и P – середины отрезков DA, DB, и DC соответственно, точка K лежит на отрезке BN. Выясните взаимное расположение прямых:
а) ND и AB; б) PK и BC;
в) MN и AB; г) MP и AC;
д) NK и AC; е) MD и BC.
а) ND ∩ AB = B, поскольку N лежит между B и D;
б) PK пересекается с BC, поскольку PK не является средней линией 
BCD и поэтому не параллельна BC (PK ∩ BC = P1).
в) MN параллельна AB, т.к. MN – средняя линия ABD. Средняя линия треугольника параллельна основанию (MN 
AB).
г) MP параллельна AC, т.к. MP – средняя линия ACD (MP AC);
д) NK и AC скрещивающиеся, т.к. они не принадлежат одной плоскости;
е) MD и BC – скрещивающиеся, т.к. не принадлежат одной плоскости.
Задача 2.
Прямая с пересекает прямую а, параллельную прямой b. Докажите, что b и c – скрещивающиеся прямые.
Дано:
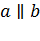
Доказать: с и b – скрещиваются
Доказательство
1. 
.
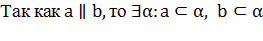Т.к., по условию задачи, 
, то через них можно провести плоскость, т.е. существует некоторая плоскость α, содержащая прямые a и b
2. 
Прямые a и c пересекаются. Обозначим точку пересечения буквой M. Так как прямые a и b параллельны, то M не принадлежит b.
3. 
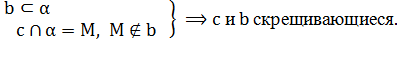Ч.т.д.
Выполняется условие: прямая b лежит в плоскости α, а прямая c пересекает эту плоскость в точке M, не лежащей на прямой b. По признаку скрещивающихся прямых прямые a и b – скрещиваются. Что и требовалось доказать.
Контрольные вопросы
1. Дайте определение скрещивающихся прямых.
2. Дайте определение параллельных прямых.
3. Дайте определение пересекающихся прямых.
4. Какие существуют варианты взаимного расположения двух прямых в пространстве.
5. Сформулируйте теоремы о скрещивающихся прямых.
6. Дайте определение сонаправленных лучей.
7. Сформулируйте теорему о равенстве углов с сонаправленными сторонами.
8. В случае пересекающихся прямых чему равен угол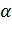 
?
Литература
1. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.].- 3-е изд.- М.: Просвещение, 2016.- 255с.
Дополнительная литература
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.