Сделать краткий конспект. Разобрать и записать все примеры.
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат - Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.
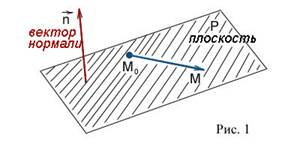
Если известна какая-нибудь точка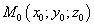 
плоскости P и какой-нибудь вектор 
нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:
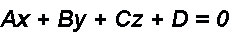
Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор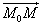 
перпендикулярен вектору 
(рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, то есть
.
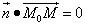Вектор задан по условию. Координаты вектора 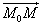найдём по формуле 
:
.
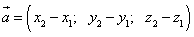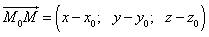Теперь, используя формулу скалярного произведения векторов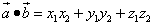 
, выразим скалярное произведение 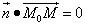в координатной форме:
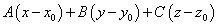. (1)
Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, 
, т.е. равенство (1) нарушается.
Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.
Пример 1. Составить уравнение плоскости, проходящей через точку 
и перпендикулярной вектору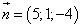 
.
Решение. Используем формулу (1), еще раз посмотрим на неё:
.
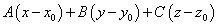В этой формуле числа A, B и C координаты вектора 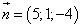, а числа x 0, y 0 и z 0 - координаты точки .
Вычисления очень простые: подставляем эти числа в формулу и получаем
.
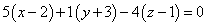Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:
.
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
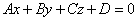(2)
называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением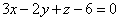 
.
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz, нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0. Поэтому получаем z = 6. Таким образом, заданная плоскость пересекает ось Oz в точке A (0; 0; 6).
Точно так же находим точку пересечения плоскости с осью Oy. При x = z = 0получаем y = −3, то есть точку B (0; −3; 0).
И, наконец, находим точку пересечения нашей плоскости с осью Ox. При y = z = 0получим x = 2, то есть точку C (2; 0; 0). По трём полученным в нашем решении точкам A (0; 0; 6), B (0; −3; 0) и C (2; 0; 0) строим заданную плоскость.
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение 
определяет плоскость, проходящую через начало координат, так как координаты точки 0 (0; 0; 0) удовлетворяют этому уравнению.
2. При A = 0 уравнение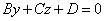 
определяет плоскость, параллельную оси Ox, поскольку вектор нормали 
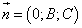этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость 
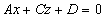параллельная оси Oy, а при C = 0 плоскость 
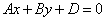параллельна оси Oz.
3. При A = D = 0 уравнение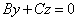 
определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость 
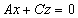проходит через ось Oy, а плоскость 
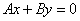через ось Oz.
4. При A = B = 0 уравнение 
определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость 
параллельна плоскости yOz, а плоскость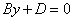 
- плоскости xOz.
5. При A = B = D = 0 уравнение 
(или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 - координатную плоскость yOz.
Пример 3. Составить уравнение плоскости P, проходящей через ось Oy и точку 
.
Решение. Итак, плоскость проходит через ось Oy. Поэтому в её уравнении y = 0 и это уравнение имеет вид 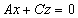. Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P.
Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (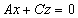). Смотрим ещё раз на координаты точки:
M 0(2; −4; 3).
Среди них x = 2, z = 3. Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
2 A + 3 C = 0.
Оставляем 2 A в левой части уравнения, переносим 3 C в правую часть и получаем
A = −1,5 C.
Подставив найденное значение A в уравнение 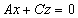, получим
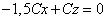или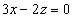 
.
Это и есть уравнение, требуемое в условии примера.