Методы оптимизации при решении инженерных задач. Условная оптимизация Критерии оптимальности.

 

3.1. Задачи оптимизации

Оптимизация - процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов, уменьшение затрат материалов, электроэнергии и т.п.

В процессе решения задачи оптимизации обычно необходимо найти оптимально выгодные значения некоторых параметров, определяющих данную задачу. При решении инженерных задач их принято называть проектными параметрами. В экономических задачах их называют параметрами плана.

В качестве проектных параметров могут быть значения линейных величин, массы, температуры и т.п. Число проектных параметров характеризует размерность задачи оптимизации.

Выбор оптимального решения или сравнение двух альтернативных решений производится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами, которая называется целевой функцией. Она является критерием качества.

В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция является глобальным критерием оптимальности в математических моделях, с помощью которой описываются инженерные или экономические задачи.

 

(3.1)

 

Следует отметить, что целевая функция не всегда может быть представлена в виде формулы. Иногда она может иметь только дискретны значения, задаваться в виде таблицы или может быть вычислена по определенно установленному правилу.

В зависимости от различных дополнительных условий задачи оптимизации делятся на две группы.

Задача безусловной оптимизации состоит в отыскании максимума (или минимума) целевой функции от п действительных переменных и определении соответствующих значений аргументов на некотором множестве Gn-мерного пространства. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих равенствам или неравенствам.

 

 

Задача условной оптимизации содержит некоторые ограничения по независимым переменным на множестве G. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих равенствам или неравенствам.

Ограничения-равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов, финансовые требования и т.п. Ограничения-неравенстваустанавливают менее жесткие зависимости между проектными параметрами, позволяя им в некоторой части области Gоставаться независимыми, а в остальной части проявляется их зависимость друг от друга.

В результате введенных ограничений область проектирования G, определяемая всеми п проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи.

Число ш ограничений-равенств может быть произвольным. Они записываются в виде:

 

(3.2)

 

Аналогично вводятся к ограничений - неравенств:

 

(3.3)

 

Следует отметить особенность в минимума целевой функции при наличии ограничений. Оптимальное решение здесь может соответствовать либо локальному экстремуму внутри области G, либо значению целевой функции на границе области G. Если ограничения отсутствуют, то находится оптимальное решение на всейобласти проектирования, т.е. определяется глобальный минимум.

 

3.2. МЕТОДЫРЕШЕНИЯ ЗАДАЧИОПТИМИЗАЦИИ

Методы решения задач оптимизации можно разделить на три группы.

3.2.1 Классический метод

Этот метод заимствован из классического математического анализа и представляет собой процедуру поиска экстремума функции многих переменных, каковой и является целевая функция (4.1). Необходимым условием существования экстремума является равенство нулю всех первых производных по всем независимым переменным или проектным параметрам. Достаточным условием существования экстремума целевой функции является положительная или отрицательная определенность матрицы-Гессиана, составленной из вторых производных.

Таким образом, сначала необходимо решить систему нелинейных уравнений:

 

(3.4)

 

Решение этой системы нелинейных уравнений - значения проектных параметров . При этих значениях целевая функция достигает максимума или минимума. Для того, чтобы определить характер экстремума, необходимо оценить Гессиан целевой функции: определенности матрицы (4.5) целевая функция имеет максимум.

Этот метод используется в случае, когда целевая функция является дважды дифференцируемой и на независимые параметры не накладывается никаких ограничений.

3.2.2. Прямые методы

Прямые методы поиска экстремума целевой функции используют значения самой функции в фиксированных точках пространства параметров G. Главная идея этих методов состоит в том, что продвижение в пространстве параметров осуществляется небольшими шагами по прямой, направленной в сторону наклона гиперплоскости, которая строится на n+1 точках, называемых симплексом данного пространства G. По мере продвижения в пространстве параметров, положение гиперплоскости постоянно изменяется и, следовательно, изменяется направление движения.

В качестве упрощенного аналога этого процесса можно привести пример шарика, расположенного на наклонной плоскости. Положение самой плоскости определяется тремя точками, соответствующими значениям целевой функции в трех точках - вершинах треугольного симплекса. Шарик начнет движение в сторону наклона плоскости, однако по мере его продвижения будет изменяться положение самой плоскости, т.к. при изменении параметров изменяются значения самой целевой функции. Таким образом, шарик с каждым шагом будет опускаться все ниже и ниже. По мере приближения к точке минимума целевой функции, положение плоскости будет приближаться к горизонтальному, вследствие чего шарик будет опускаться все медленнее и медленнее и, наконец, достигнув точки минимума целевой функции, остановится на горизонтальной плоскости.

Такая процедура реализована в симплекс-методе Нелдера-Мида, который является достаточно надежным при п меньше или равным шести. Рассмотрим в основных чертах алгоритм этого метода.

Регулярным симплексом в n-мерном пространстве называется множество п+1 равноудаленных точек. В двумерном пространстве, т.е. на плоскости, регулярным симплексом является равносторонний треугольник, а в трехмерном пространстве - правильный тетраэдр и т.д. Идея метода состоит в сравнении значений функции в (п+1)-й вершинах симплекса и перемещении симплекса в направлении точки минимума целевой функции с помощью итерационной процедуры, которая использует три основные операции: отражение, растяжение и сжатие. Рассмотрим данную процедуру подробно по шагам.

1. Найдем значения целевой функции в вершинах симплекса, тогда будем иметь

:

(3.6)

 

где - вершины симплекса.

2. Из всех значений выберем следующие:

u_h - наибольшее из всех значений (4.6) целевой функции,

u_g- следующее по величине значение целевой функции после u_h.

u_l- наименьшее из всех значений (4.6).

Этим трем значениям целевой функции соответствуют точки x_h,x_g,x_{, гдеХ=(х₁,х₂,..., x_n).

3. Исключив из множества , точку х_h, найдем и вычислим значение функции

4. Проведем прямую через точки x_h и х₀; на этой прямой возьмем точку x_r поформуле:

 

(3.8)

 

и в этой точке вычислим значение целевой функции

5. Сравним значения функций f_r и f _l.

5.1 Если f_r меньше f _l, то мы получили наименьшее значение функции в точке х_г. Значит нам надо продвигаться от точки х₀ в сторону х_г до точки х_е, которую найдем поформуле:

 

(3.9)

 

5.1.1. Если f_в меньше f_l, то заменяем точку x_h на х_е и проверяем процесс на сходимость к минимуму.Если сходимость достигнута, то процесс останавливаем, если нет - то переходим на 5.1.2.

5.1.2. Если f_в больше f_l, то отбрасываем точку f _g. Теперь мы продвинулись достаточно далеко от точки х₀ к точке х_г, поэтому следует заменить точку x_h на точку х_г,в которой было достигнуто уменьшение значения целевой функции. Здесь опять нужно проверить сходимость к минимуму, и если она достигнута, перейти на 3.

5.2. Если f _вбольше f _l, но f _r меньше и равно f_g, тох_r является лучшей точкой по сравнению с другими двумя точкамисимплекса и тогда следует точку x_h заменить на точку х_г,и если сходимость достигнута, перейти на 2.

5.3. Если f_r больше f_h и / то перейдем на 6.

6. Сравним значения функций f_rи f_h.

6.1. Если f_r больше f_h, то переходим к 6.2. Если f_r меньше f _h, то заменяем точку x_h на x_r и значение функции f_h, на f_r. Запоминаем значение функции f_r,больше чем f_g из пункта 5.2 и переходим на 6.2.

6.2. В этом случае /_г больше /_й, поэтому ясно, что мы продвинулись слишком далеко вдоль по прямой x_h — х₀, очевидно здесь необходимо сделать шаг назад в

точку х_с по формуле:

 

(3.10)

 

 

0< d <1 - коэффициент сжатия.

Если f_r меньше f_h, то сначала заменим точку x_h на точку х_r, а затем произведем сжатие, т.е. продвинемся назад в новую точку по формуле:

 

(3.11)

 

 

7. Сравниваем значения функций f_c и f_h.

7.1. Если f_c меньше f_h, то заменяем точку x_h на x_c, и если сходимость достигнута, перейти на 2.

7.2. Если f_c больше x_h, то очевидно, что мы недобились уменьшения целевой функции, поэтому необходимо перейти к пункту 8.

8. На этом шаге мы уменьшаем размеры симплекса делением пополам расстояния от каждой вершины симплекса до точки х_г, где зафиксировано наименьшее значение целевой функции.

Таким образом, точки заменяются на новые точки bi по формуле:

 

(3.12)

 

Затем вычисляются значения целевой функции f в новых вершинах bi, (i= 1,2, …,п+1), проверяем сходимость и, если она не достигнута, переходим на 3.

9. Проверка сходимости основана на том, чтобы стандартное отклонение целевой функции в (n+ 1)- ой вершине симплекса от средне-квадратического по другим вершинам было меньше некоторой заданной малой величины. Оценка производится по формулам:

 

	(3.13)
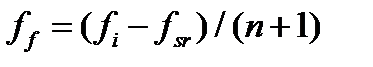
	(3.14)

Если f_f меньше Е, то все значения целевой функцииочень близки друг к другу, и поэтому они, возможно, лежат вблизи точки минимума.

Коэффициенты a,b,d в вышеприведенной процедуре называются соответственно коэффициентами отражения, сжатия и растяжения. Данным коэффициентам рекомендуется задавать следующие значения: a=1,b=0.5,d=2.

Начальный симплекс выбирается произвольно, исходя из конкретного содержания решаемой задачи. Точка Al является исходной, тогда:

где к - произвольная постоянная, ei- единичный вектор.

Графическая иллюстрация поиска минимума целевой функции, определяемой двумя независимыми переменными параметрами, представлена на рисунке 3.1.

Рисунок 3.1.

 

3.2.3. Градиентные методы

В этих методах наряду со значениями самой целевой функции используется и ее градиент, и таких методов разработано достаточно много: метод наискорейшегоспуска, метод сопряженных градиентов и другие их модификации. Общим для этих методов является ис­пользование градиента для продвижения в пространстве параметров G.

Направление градиента является направлением наискорейшего возрастания функции, следовательно противоположное направление является направлением наискорейшего убывания функции. В целях упрощения графической иллюстрации сначала рассмотрим целевую функцию двух независимых параметров:

 

(3.15)

 

Графиком этой функции является некоторая криволинейная поверхность, которая имеет "возвышения" и "впадины". Нашей целью является попадание в одну из "впадин", которая будет по расположению самой низшей по высоте из всех остальных. Координаты самой низкой точки этой "впадины" будут являться решением задачи оптимизации.

Если эту поверхность рассечь семейством горизонтальных плоскостей, расположенных на разных уровнях, то в сечениях будут получены кривые линии, называемые линиями равного уровня, которые тоже образуют семейство замкнутых и разомкнутых кривыхлиний. Форма этих линий характеризует поверхность целевой функции.

Градиентом является вектор:

 

(3.16)

 

Где - вектор - столбец независимыхпараметров, - единичные векторы,

- частные производные целевой функции

Вектор градиента перпендикулярен к линиям уровня и направлен в сторону выпуклости линии уровня для "впадины" и в сторону вогнутости для "возвышения" (см. рис. 3.2.). Таким образом, постоянное продвижение против градиента должно привести к решению поставленной задачи; однако, по мере продвижения в пространстве параметров G, градиент меняет свое направление, поэтому необходимо соблюдать разумную стратегию продвижения вдоль первоначально фиксированного направления градиента в исходной базовой точке, откуда совершается первый шаг. Например, находясь в точке М₀, мыфиксируем направления продвижения по прямой, направленной против градиента g(Mo). Сделав несколькошагов, мы можем оказаться в точках либо либо или .

Наиболее предпочтительным оказывается попадание в точку , т.к. значение функции в ней наименьшее. Следующий подобный шаг будет сделан перпендикулярно линии уровня в сторону вогнутости, так чтобы из всех точек фиксированной прямой, направленной против градиента g(M2), была выбрана точка, в которой значение целевой функции наименьшее. Такая итерационная процедура продолжается до тех пор, пока модуль приращения функции не станет меньше наперед заданного положительного малого числа.

Рисунок 3.2. Линии уровня и градиент целевой функции

 

Рассмотренный алгоритм позволяет достаточно легко отыскивать точку минимума целевой функции, поверхность которой имеет выпуклую форму или в таком случае целевая функция является унимодальной. Ситуация осложняется, когда функция не является унимодальной, например ее поверхность имеет "овражную" форму. Линии уровня такой функции приведены на рис. 4.3.

Поверхность такой функции имеет сложную форму: имеется центральное "русло", которое протягивается на большое расстояние, в сочетании с извилинами и, в худшем случае, с очень небольшим понижением, временами переходящими в локальные "впадины". К центральному "руслу" подходят боковые "русла", которые имеют аналогичное строение.

Очевидно, что рассмотренная процедура поиска минимума для целевой функции "овражного" типа может оказаться непригодной или могут возникнуть большие проблемы; в лучшем случае могут резко увеличиться затраты времени на счет.

Для поиска минимума целевой функции "овражного типа" существует модификация метода наискорейшего спуска с промежуточной поправкой направления продвижения. Идея этого метода заключается в том, что для продвижения в пространстве параметров Gиспользуется скорректированное направление градиента.

Рисунок 3.3. Линии уровня функции "овражного" типа

 

Начиная с первого шага, по всем параметрам проверяется величина приращения целевой функции и, если она будет меньше определенной величины, то продвижения по этой переменной не должен быть. Причем такая проверка производится с помощью шагов большой величины, что позволяет нащупывать направление главного "русла" оврага. Заметим, что в данном случае градиент направлен почти перпендикулярно главному "руслу" овражнойфункции, а корректировка направления градиента позволяет продвигаться вдоль главного "русла" оврага.

Дальнейшее продвижение по выбранному направлению осуществляется постоянными или переменными возрастающими шагами до тех пор, пока целевая функция будет убывать. В случае возрастания функции производится шаг назад в предпоследнюю точку.

В этой точке определяется новое направление продвижения, и весь процесс итерационно повторяется снова. Поиск заканчивается, если модуль приращения целевой функции будет меньше наперед заданной малой величины.

Рассмотрим изложенный алгоритм детально по шагам.

1.Введем начальные значения параметров

Вычислим значение функции

2.Определим направление градиента g(X₀).

 

(3.17)

 

3.Определяем скорректированное направление градиента. Для этого каждой переменной xi даем большое приращение di по отдельности и, если приращение функции будетбольше наперед заданной конечной величины, то эту переменную надо зафиксировать или положить е, = О, иначе е; = 1. Тогда скорректированный градиент имеет вид:

 

(3.18)

 

 

4.Начинаем продвижение в направлении противоположном скорректированному градиенту по формуле:

 

(3.19)

 

 

Вычислим значение функции fj=f (Xj).

5. Если fj<fo, то j= j+1 и перейдем к пункту 3.

Если fj>fo, то точку Хо заменим на Xj. Произведем проверку на сходимость.

6. Проверка на сходимость заключается в следующем. В последней точке Xjвычисляется приращение функции от всех переменных:

 

(3.20)

 

где Н - вектор - столбец приращений переменной Х = (х₁,х₂,...,х_п).

7. Если меньше eps- наперед заданной малой величины, то процесс завершаем. Если больше eps, то перейдем к пункту 2.