3.1. Пример статистической обработки малой (
=20) выборки
3.1.1. Постановка задачи и исходные данные
Для заданной статистической выборки, состоящей из 20 измерений (числа измерений базового размера изделия в мм), приведенных в таблице 5, выполнить статистическую обработку результатов измерений и произвести оценку полученных результатов.
Таблица 5 – Заданная малая выборка
| № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины. |
| 43.4 | 45.2 | 44.6 | 46.2 | ||||
| 43.6 | 45.3 | 44.7 | 46.2 | ||||
| 44.3 | 45.6 | 44.7 | 46.8 | ||||
| 44.5 | 45.8 | 44.8 | 47.2 | ||||
| 44.5 | 45.8 | 45.1 | 47.7 |
3.1.2. Статистическая обработка результатов измерений
Располагая заданные результаты в порядке их возрастания, получим ранжированный вариационный ряд, приведенный в таблице 6.
Таблица 6 – Ранжированный ряд малой выборки
| № опыта | Значение
| Разность
- 
| Квадрат
разности
( - )2
| № опыта | Значение
| Разность
-
| Квадрат
разности
( - )2
|
| 43.4 | -1.9 | 3.61 | 45.3 | 0.0 | 0.00 | ||
| 43.6 | -1.7 | 2.69 | 45.6 | 0.3 | 0.09 | ||
| 44.3 | -1.0 | 1.0 | 45.8 | 0.5 | 0.25 | ||
| 44.5 | -0.8 | 0.64 | 45.8 | 0.5 | 0.25 | ||
| 44.5 | -0.8 | 0.64 | 46.2 | 0.9 | 0.81 | ||
| 44.6 | -0.6 | 0.49 | 46.2 | 0.9 | 0.81 | ||
| 44.7 | -0.6 | 0.36 | 46.8 | 1.5 | 2.25 | ||
| 44.7 | -0.5 | 0.36 | 47.2 | 1.8 | 3.61 | ||
| 44.8 | -0.5 | 0.25 | 47.7 | 2.4 | 5.76 | ||
| 45.1 | -0.2 | 0.04 | Сумма | ∑=906 | ∑=0 | ∑=24.12 | |
| 45.2 | -0.1 | 0.01 |
Суммируя значения ранжированного вариационного ряда, определяем выборочное среднее
= 
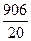=45.3 мм.
В графе 3 приведены разности между каждой составляющей выборки и выборочным средним , а в графе 4 их квадраты. Суммируя их найдем дисперсию выборки
= 
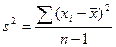=1.269.
Для оценки рассеивания случайной величины относительно математического ожидания используются следующие характеристики: среднее квадратичное отклонение, коэффициент вариации, показатель точности и доверительный интервал.
Выборочное среднее квадратическое отклонение определяем по формуле
= 
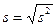=1.127.
Среднее квадратическое отклонение сводного результата определяем по формуле
= 
=0.252.
Выборочный коэффициент вариации определяем по формуле
= 
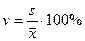∙100%=2.487%.
Коэффициент вариации показывает, как велико рассеивание результатов в сравнении со средним значением.
Показатель точности определяем по формуле
= 
∙100%=0.556%.
Показатель точности свидетельствует о точности методики, по которой проводились испытания и получены результаты.
Доверительный интервал выборочных характеристик можно определить при помощи критерия Стьюдента по формуле
- 
∙ 
+ ∙ ,
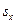
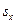где - критерий Стьюдента для уровня доверительной вероятности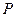 
, обычно принимаемой равной 0.95 или 0.99, и числа степеней свободы 
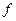=n-1 принимают по статистическим таблицам. Они имеются практически в каждом руководстве по математической статистике. В нашем случае:
а) при 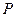=0.95 и 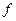=20-1=19 получим 45.3-2.095∙0.252 45.3+2.095∙0.252 и после вычислений 44.77 мм 45.83 мм,
б) при 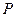=0.99 и 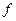=20-1=19 получим 45.3-2.859∙0.252 45.3+2.859∙0.252 и после вычислений 44.58 мм 46.02 мм.
То есть с увеличением уровня доверительной вероятности 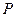доверительный интервал расширяется (45.83-44.77=1.06 мм и 46.02-44.58=1.44 мм).
Проверим теперь принадлежность первого и последнего результатов испытаний (ранжированного вариационного ряда) той же генеральной совокупности, как и остальные 18 результатов. Так как выборка имеет малый объем (n=20), то проверку можно провести при помощи критерия Груббса. Для этого определяют:
а) для первого результата измерений 
= 
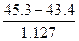=1.686;
б) для последнего результата измерений 
= 
=2.13.
Так как и 
=1.686 и 
=2.13 значительно меньше табличного (критического) значения (при 
=0.05 и n=20 è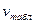 
=2.623), то нулевая гипотеза подтверждается [5].
3.2. Пример статистической обработки большой (N=80) выборки
3.2.1. Постановка задачи и исходные данные
Для заданной статистической выборки, состоящей из 80 измерений (числа измерений базового размера изделия в мм), приведенных в таблице 7, выполнить статистическую обработку результатов измерений и произвести оценку полученных результатов.
Таблица 7– Заданная большая выборка
| № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины |
| 31.4 | 30.6 | 39.1 | 42.6 | 34.5 | |||||
| 30.6 | 31.7 | 38.5 | 41.8 | 38.2 | |||||
| 30.3 | 32.2 | 38.2 | 34.6 | 35.4 | |||||
| 31.5 | 32.1 | 36.1 | 42.7 | 36.2 | |||||
| 32.5 | 30.9 | 38.2 | 41.7 | 37.1 | |||||
| 30.0 | 34.3 | 42.4 | 43.8 | 40.0 | |||||
| 31.3 | 34.6 | 39.4 | 40.1 | 43.1 | |||||
| 30.0 | 33.9 | 40.7 | 38.0 | 42.7 | |||||
| 31.6 | 32.3 | 41.6 | 38.3 | 41.6 | |||||
| 30.9 | 35.2 | 41.1 | 37.5 | 39.3 | |||||
| 31.6 | 35.3 | 39.7 | 39.3 | 44.4 | |||||
| 31.4 | 35.6 | 37.0 | 39.0 | 36.2 | |||||
| 32.8 | 35.8 | 42.0 | 38.0 | 43.2 | |||||
| 32.4 | 36.8 | 38.3 | 35.4 | 36.8 | |||||
| 32.0 | 39.4 | 32.5 | 35.6 | 37.2 | |||||
| 30.9 | 39.6 | 37.3 | 35.8 | 43.7 |
3.2.2. Статистическая обработка результатов измерений
Вначале располагаем результаты наблюдений по мере их возрастания (таблица 8 – ранжированный вариационный ряд) и определяем наименьшее и наибольшее значения приведенной выборки: 
= 30.0 мм,
= 44.4 мм.
Таблица 8 – Ранжированный ряд большой выборки
| № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины | № опыта | Значение случайной величины |
| 30.0 | 32.1 | 35.6 | 38.2 | 40.7 | |||||
| 30.0 | 32.2 | 35.6 | 38.2 | 41.1 | |||||
| 30.3 | 32.3 | 35.8 | 38.2 | 41.6 | |||||
| 30.6 | 32.4 | 35.8 | 38.3 | 41.6 | |||||
| 30.6 | 32.5 | 36.1 | 38.3 | 41.7 | |||||
| 30.9 | 32.5 | 36.2 | 38.5 | 41.8 | |||||
| 30.9 | 32.8 | 36.2 | 39.0 | 42.0 | |||||
| 30.9 | 33.9 | 36.8 | 39.1 | 42.4 | |||||
| 31.3 | 34.3 | 36.8 | 39.3 | 42.6 | |||||
| 31.4 | 34.5 | 37.0 | 39.3 | 42.7 | |||||
| 31.4 | 34.6 | 37.1 | 39.4 | 42.7 | |||||
| 31.5 | 34.6 | 37.2 | 39.4 | 43.1 | |||||
| 31.6 | 35.2 | 37.3 | 39.6 | 43.2 | |||||
| 31.6 | 35.3 | 37.5 | 39.7 | 43.7 | |||||
| 31.7 | 35.4 | 38.0 | 40.0 | 43.8 | |||||
| 32.0 | 35.4 | 38.0 | 40.1 | 44.4 |
Определяем размах варьирования результатов измерений
= - =44.4-30.0=14.4 мм
и задавшись числом интервалов 
=9 (часто число интервалов берут равным 7, 9 или 11, чтобы интервалы были достаточно наполнены частотами), устанавливаем ширину интервала
= 
= 
=1.6 мм.
За ширину интервала принимаем h =1.7 (некоторое увеличение ширины интервала способствует перекрыть правую границу размаха варьирования). Для того, чтобы избежать совпадения отсчетов с границами интервалов при группировке отдельных значений, рекомендуется отступать на половину интервала (0.5 h) влево от нижнего предела варьирования:
= -0.5∙ h =30.0-0.5∙1.7=29.15 мм.
Определяем числовые характеристики заданных случайных величин. Интервальный ряд и его характеристики сводим в таблицу 9. Частость и плотность определялись в соответствии указанных в таблице 9 формул.
Таблица 9 – Интервальный ряд и его характеристики
| Интервалы | Частота m | Накопленная частота mнак | Частость w=m/n | Накопленная частоcть w | Плотность рас-пределения m/h |
| 29.15-30.85 | 0.0625 | 0.0625 | 2.941 | ||
| 30.85-32.55 | 0.2125 | 0.275 | 10.0 | ||
| 32.55-34.25 | 0.025 | 0.3 | 1.176 | ||
| 34.25-35.95 | 0.15 | 0.45 | 7.059 | ||
| 35.95-37.65 | 0.125 | 0.575 | 5.882 | ||
| 37.65-39.35 | 0.15 | 0.725 | 7.059 | ||
| 39.35-41.05 | 0.0875 | 0.8125 | 4.118 | ||
| 41.05-42.75 | 0.125 | 0.9375 | 5.882 | ||
| 42.75-44.45 | 0.0625 | 1.0 | 2.941 | ||
| Сумма | - | 1.000 | - | - |
В таблице 10 выполним вычисления, необходимые для определения выборочных статистик. Последовательность проводимых вычислений ясна из таблицы 6.
Таблица 10 – Интервальный ряд и его статистические характеристики
| № п.п. | Интервал a-b | Средина интервала yj | Частота mj |
|
|
|
|
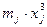
| 29.15-30.85 | 30.00 | 150.0 | 4500.0 | ||||
| 30.85-32.55 | 31.70 | 538.9 | 17083.1 | ||||
| 32.55-34.25 | 33.40 | 66.8 | 2231.1 | ||||
| 34.25-35.95 | 35.10 | 421.2 | 14784.1 | ||||
| 35.95-37.65 | 36.80 | 368.0 | 13542.4 | ||||
| 37.65-39.35 | 38.50 | 462.0 | 17787.0 | ||||
| 39.35-41.05 | 40.20 | 281.4 | 11312.3 | ||||
| 41.05-42.75 | 41.90 | 419.0 | 17556.1 | ||||
| 42.75-44.45 | 43.60 | 218.0 | 9504.8 | ||||
| Сумма | 2925.3 |
Вычислим выборочное среднее значение искомого линейного размера по формуле (2)
= 
=36.566 мм.
Далее вычисляем дисперсию, среднее квадратичное отклонение, коэффициент вариации, показатель точности и доверительный интервал:
- дисперсия 
=
= 
[108301- 
·(2925.3)2]= 16.882 мм2.
- среднее квадратичное отклонение =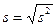 
=4.109 мм,
- коэффициент вариации =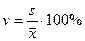 
, который характеризует относительное рассеивание случайной величины относительно среднего.
- показатель точности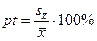 
= 
∙100%=1.26%, где 
- средняя квадратическая ошибка сводного результата измерений или стандарт арифметической средней, который равен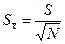 
= 
=0.4594.
- доверительный интервал выборочных характеристик можно определить при помощи критерия Стьюдента по формуле
- 
∙ 
+ ∙ ,
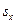
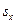где - критерий Стьюдента для уровня доверительной вероятности 
обычно принимаемой равной 0.95 или 0.99 и числа степеней свободы k=n-1 находится по статистическим таблицам. В нашем случае:
а) при 
=0.95 и k=80-1=79 получим 36.566-1.990∙0.4594 36.566+1.990∙0.4594 и после вычислений 35.65 мм 37.48 мм,
б) при =0.99 и k=80-1=79 получим 36.566-3.639∙0.4594 36.566+3.639∙0.4594 и после вычислений 34.89 мм 38.24 мм.
То есть с увеличением уровня доверительной вероятности доверительный интервал расширяется (37.48-35.65=1.83 мм и 38.24-34.89=3.35 мм).
Определяем структурные средние выборки – медиану (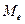
) и моду (
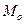). Медиана – это среднее значение ранжированного ряда. Для нечетного числа наблюдений ранжированного ряда она равна значению измерения, занимающего серединное положение. Для четного числа измерений ранжированного ряда она равна среднему арифметическому значению двух измерений, занимающих серединное положение. В нашем случае
= 
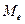=36.8.
Для интервального ранжированного вариационного ряда медиану можно определить по приближенной формуле, но удобнее это выполнить графическим способом. Для этого строится кумулятивная кривая
Мода – это наиболее часто встречающееся измерение в ранжированном вариационном ряду.
Проведем проверку нулевой гипотезы. Проверим принадлежность первого и последнего результатов ранжированного вариационного ряда той же генеральной совокупности, как и остальные 78 результатов. Так как выборка имеет большой объем (n>25), то проверку можно провести при помощи критерия Ирвина. Для этого вычислим значение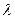 
для первого и последнего результатов ранжированного вариационного ряда:
= 
= 
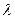=0.073,
= 
= 
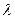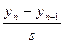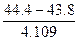=0.146, что значительно меньше критического значения (из таблицы 4 [5] для N=80 и любой вероятности 
è 
>0.84). Так как найденные значения 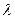для первого-второго и последнего результатов ранжированного вариационного ряда меньше 
>0.84, то нулевая гипотеза подтверждается и найденные ранее числовые статистические характеристики распределения не подвергаются корректировке.
Аналогично можно провести проверку нулевой гипотезы по t-критерия Стьюдента. Вычислим величину критерия по формуле (15)
= 
= 
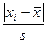=1.907 и сравниваем его с критическим значением t-критерия Стьюдента, найденной по статистическим таблицам по выбранному уровню значимости 
=0.05 и числу степеней свободы 
= -1=80-1=79 (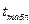
=1.99). Так как =1.907 
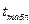=1.99, то проверяемый результат не исключается из выборки и ранее найденные числовые характеристики распределения не подвергают корректировке.
Замечание. Для наглядности можно построить гистограмму и кривую распределения или кривую плотности вероятностей. Они является графиком соотношения между значениями данной случайной величины и их вероятностями. В теории вероятности это соотношение называется статистическим распределением. Известны много видов распределения, но наиболее часто применяется нормальное (гауссовское) распределение, играющее важную роль в теории вероятностей и математической статистике. На рисунке изображены гистограмма для большой выборки и нормальная кривая распределения (кривая Гаусса). Порядок их построения следующий:
I-гистограмма. По оси абсцисс откладываются в выбранном масштабе все интервалы, а по оси ординат, тоже в выбранном масштабе, частости по каждому из интервалов (заштрихованные прямоугольники на диаграмме).
II-кривая нормального распределения. От центра распределения (вершины кривой) влево и вправо откладываются три характерные точки кривой нормального распределения: 
; ±S; ±2S; ±3S. Затем для этих характерных точек вычисляются ординаты (теоретические частоты) кривой нормального распределения по формулам:
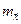=0.4· 
=0.4· 
=13.24,
=0.242· =0.242· =8.01,
Рисунок – Гистограмма и кривая нормального распределения
=0.054·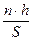 
=0.054· =1.79,
=0.
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. / Гмурман В.Е. 11-е изд. стереотипное -М.: Высшая школа, 2005. -480с.
2. Митропольский А.К. Техника статистических вычислений. /А.К. Митропольский 2-е изд. прераб. и дополн. -М.: Наука, 1971. -576с.
3. Ивченко Г.И. Математическая статистика. Учебное пособие для вузов. /Г.И. Ивченко, Ю.И. Медведев. -М.: Высшая школа, 1984. -248с.
4. Пижурин А.А. Основы научных исследований в деревообработке. /А.А. Пижурин, А.А. Пижурин. –М.: изд. МГУЛ, 2007. -305с.
5. Казаринова М.Е. Статистический анализ в научных работах. Методическое пособие. /М.Е. Казаринова, Л.Н. Тепман, В.И. Клепов, И.Н. Каплан. Приок. книж. изд. Брянск, 1976. -71с.
6. Казаринова М.Е. Статистический анализ в технологических исследованиях. /М.Е. Казаринова, Л.Н. Тепман, А.И. Кузовков. Приок. книж. изд. Брянск, 1978. -206с.