Законы Кирхгофа в комплексной форме.

2.1. Первый закон Кирхгофа (для узла): алгебраическая сумма комплексных амплитуд тока в узле равна нулю.

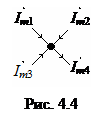При записи первого закона Кирхгофа (рис. 4.4) пользуются следующим правилом: токи, втекающие в узел, берутся со знаком «+», а вытекающие – со знаком «–»:

.

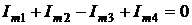2.2. Второй закон Кирхгофа (для контура): алгебраическая сумма падений напряжений на пассивных элементах контура (рис. 4.5) равна алгебраической сумме источников ЭДС, входящих в контур:

.

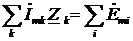При составлении уравнений по второму закону Кирхгофа:

1) выбирают условно-положительное направление обхода элементарного контура;

2) члены суммы 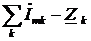берутся со знаком «+», если ток через элемент и направление обхода совпадают, и со знаком «–» в противном случае;

3) слагаемые правой суммы 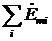берутся со знаком «+», если направление источника ЭДС и направление обхода совпадают, и со знаком «–» в противном случае.

 

4.3. Эквивалентные преобразования электрических цепей

Часто исходная электрическая схема состоит из большого числа элементов и представляет интерес замены, т.е. преобразования ее к более простой – состоящей из меньшего числа элементов, но эквивалентной исходной. Преобразования электрических цепей считают эквивалентными, если при их выполнении напряжения и токи на интересующих нас участках не изменяются.

Электрические цепи считают простыми, если они содержат только последовательное или только параллельное соединение элементов.

Участок цепи, содержащий и параллельное, и последовательное соединение элементов называют сложным или участком со смешанным соединением элементов.

При преобразовании сложных электрических цепей пользуются последовательным методом, то есть последовательно преобразуют участки цепи, имеющие простое соединение элементов.

 

4.3.1. Эквивалентное преобразование схемы при последовательном
соединении элементов

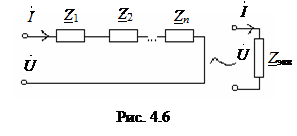Рассмотрим комплексную схему замещения электрической цепи, состоящей из последовательного соединения отдельных элементов (рис. 4.6). Данная цепь представляет собой контур, у которого через все элементы протекает общий для всех элементов ток. Эквивалентно преобразуем схему к одному элементу, но так, чтобы напряжение и ток на выводах схемы сохранили свои значения. Это возможно, когда сопротивление исходной и эквивалентной цепи одинаковы. На основании закона Ома и второго закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия

.

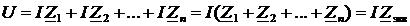Отсюда напряжение и ток для обеих схем одинаковы когда

.

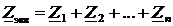Вывод. При эквивалентном преобразовании при последовательном соединении элементов их комплексные сопротивления складываются.

1) Эквивалентное преобразование сопротивлений.

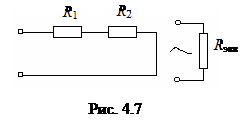Рассмотрим электрическую цепь, схема которой приведена на рис. 4.7. Эквивалентно преобразуем сопротивления R ₁ и R ₂ к одному сопротивлению R _экв.

Учитывая, что Z _R = R, и полученное соотношение, имеем R _экв = R ₁ + R ₂.

 

2) Эквивалентное преобразование емкостей.

Рассмотрим электрическую цепь, схема которой приведена на рис. 4.8. Эквивалентно преобразуем емкости С ₁ и С ₂ к одной эквивалентной емкости С _экв.

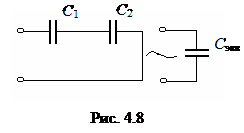Учитывая, что Z _С = 1/(j ω C), и полученное соотношение, имеем

 

.

 

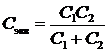3) Эквивалентное преобразование индуктивностей.

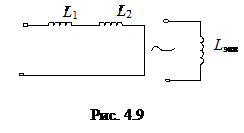Рассмотрим электрическую цепь схема, которой приведена на рис. 4.9. Эквивалентно преобразуем индуктивности L ₁ и L ₂ к одной эквивалентной индуктивности L _экв.

Учитывая, что Z _L = j ω L, и полученное соотношение, имеем L _экв = L ₁ + L ₂.

 

4.3.2. Эквивалентное преобразование схемы при параллельном
соединении элементов

Рассмотрим комплексную схему замещения электрической цепи, состоящей из параллельного соединения отдельных элементов (рис. 4.10). Данная цепь содержит два узла, между которыми включены все элементы. Общим для всех элементов является напряжение на них. Эквивалентно преобразуем схему к одному элементу, но так, чтобы напряжение и ток на выводах схемы сохранили свои значения. Это возможно, когда сопротивление исходной цепи и эквивалентной цепи одинаково. На основании закона Ом 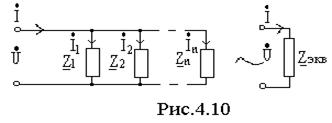а и первого закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия

I = I ₁+ I ₂+…+ I_n, или (U / Z _экв) = (U / Z ₁) + (U / Z ₂) + … +(U / Z _n).

Отсюда следует, что

(1/ Z _экв) = (1/ Z ₁) + (1/ Z ₂) + … +(1/ Z _n), или Z _экв = 1/[(1/ Z ₁) + (1/ Z ₂) + … +(1/ Z _n)].

Учитывая, что (1/ Z) = Y – комплексная проводимость элемента, можно записать

Y _экв = Y ₁ + Y ₂ + … + Y _n.

Вывод. При эквивалентном преобразовании при параллельном соединении элементов их комплексные проводимости складываются.

1) Эквивалентное преобразование сопротивлений.

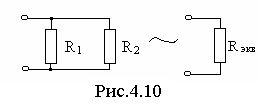Рассмотрим электрическую цепь, схема которой приведена на рис. 4.10. Эквивалентно преобразуем сопротивления R ₁ и R ₂ к одному сопротивлению R _экв.

Учитывая, что Z _R = R, и полученное соотношение, получим R _экв = R ₁ R ₂/(R ₁+ R ₂).

2) Эквивалентное преобразование емкостей.

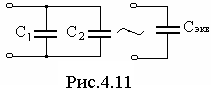Рассмотрим электрическую цепь, схема которой приведена на рис. 4.11. Эквивалентно преобразуем емкости С ₁ и С ₂ к одной эквивалентной емкости С _экв. Учитывая, что Z _С = 1/(j ω C), и полученное соотношение, имеем C _экв = C ₁ + С ₂ .

3) Эквивалентное преобразование индуктивностей.

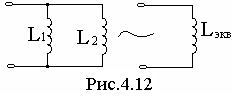Рассмотрим электрическую цепь, схема которой приведена на рис. 4.12. Эквивалентно преобразуем индуктивности L ₁ и L ₂ к одной эквивалентной индуктивности L _экв.

Учитывая, что Z _L = j ω L, и полученное соотношение, имеем L _экв = L ₁ L ₂/(L ₁+ L ₂).

 

4.3.3. Эквивалентное преобразование схемы при смешанном
соединении элементов

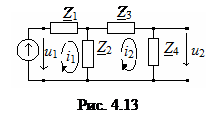Такое преобразование выполняется последовательным методом, т.е. последовательно преобразуются участки цепи, имеющие простое соединение элементов. Рассмотрим такое преобразование на примере для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис. 4.13).

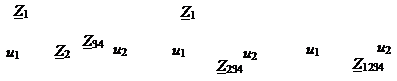Эквивалентное сопротивление находим методом последовательных эквивалентных преобразований. Этот методсостоит в поэтапном преобразовании простых участков цепи. Они показаны на рис. 4.14:

Z 34 =Z 3+ Z 4, Z 234 = Z 34 Z 2/(Z 34+ Z 2), Z 1234 = Z 1 + Z 234 = Z экв.

а б в

Рис. 4.14

 

4.3.4. Эквивалентное преобразование источников электрических сигналов

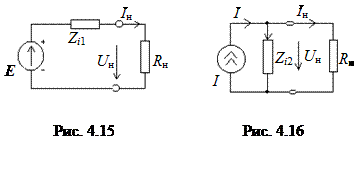Любой источник электричес-кого сигнала может быть представлен одной из двух схем (рис. 4.15–4.16), поскольку при определенном выборе параметров элементов эти схемы эквивалентны, т.е. ток нагрузки I _н и напряжение на нагрузки U _н в этих схемах одинаковы.

Схему 1 можно заменить схемой 2, если параметры схемы 2 выбраны из условий: I = E / Z _{i 1}, Z _{i 2} = Z _{i 1}.

Схему 2 можно заменить схемой 1, если параметры схемы 1 выбраны из условий: E = I Z _{i 1}, Z _{i 1} = Z _{i 2}.

 

4.4. Классификация электрических цепей

В общем случае, когда схема электрической цепи неизвестна, недоступна или нас не интересует, ее изображают в виде прямоугольника с рядом выводов (полюсов) схемы, с помощью которых она соединяется с другими устройствами.

1. В зависимости от числа выводов (полюсов) электрические цепи делятся на двухполюсники, четырехполюсники, многополюсники (рис. 4.17)

21

11

n

Рис. 4.17

2.В зависимости от характера элементов, входящих в электрическую цепь, различают:

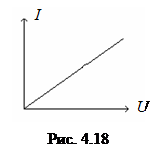1) Линейные цепи. Это цепи, которые состоят только из линейных элементов, т.е. элементов, параметры которых не зависят от токов и напряжений на них. Все линейные элементы имеют линейные вольт-амперные характеристики (рис. 4.18).

Процессы в таких цепях описываются линейными дифференциальными уравнениями с постоянными коэффициентами.

2) Нелинейные цепи. Это цепи, которые содержат
нелинейные элементы, т.е. элементы, параметры которых зависят от токов и напряжений на них. Все нелинейные элементы имеют нелинейные вольт-амперные характеристики (рис. 4.19). Процессы в таких цепях описываются
нелинейными дифференциальными уравнениями с постоянными коэффициентами.

3) Параметрические цепи. Это цепи, в состав которых входят параметрические элементы, т.е. элементы, параметры которых изменяются во времени (например, микрофоны). Процессы в таких цепях описываются нелинейными дифференциальными уравнениями с переменными коэффициентами.

3. В зависимости от соотношения длины электромагнитной волны λ и геометрических размеров электрической цепи L различают цепи с сосредоточенными и распределенными параметрами.

λ – это путь, который проходит волна за период T.

λ = cT = c / ¦, где c – скорость света, ¦ – частота. Длина волны зависит от частоты сигнала.

а) Если λ >> L, то цепи называются цепями с сосредоточенными параметрами. В них все процессы преобразования энергии сосредоточены в элементах.

В таких цепях токи и напряжения в различных сечениях цепи зависят только от времени и не зависят от координаты сечения х. Процессы в таких цепях описываются дифференциальными уравнениями в полных производных.

б) Если λ ≤ L, то цепи называются цепями с распределенными параметрами. В них элементы R, L, C необходимо рассматривать распределенными в пространстве.

Токи и напряжения в таких цепях зависят не только от времени, но и от координаты. Процессы в таких цепях описываются дифференциальными уравнениями в частных производных.

4.В зависимости от наличия в цепях активных элементовразличают пассивные и активные цепи. Активные цепи содержат источники (активные элементы), а пассивные их не содержат. Активные цепи делят на автономные и неавтономные. Автономные цепи содержат независимые источники, а неавтономные содержат только зависимые источники.

 

Основные режимы работы электрических цепей

 

В зависимости от частоты выделяют следующие режимы работы цепей:

1) при постоянных ЭДС и токах;

2) при переменных ЭДС и токах.

В зависимости от характера протекающих в цепи электромагнитных процессов различают установившийся (стационарный) режим и переходной
(нестационарный) режим.

В зависимости от нагрузки различают четыре основных режима работы:

1) номинальный;

2) согласованный;

3) холостого хода;

4) короткого замыкания.

При номинальном режиме все устройства данной цепи работают в нормальных для них условиях.

Согласованным называют режим передачи от источника к приемнику наибольшего количества энергии или режим выделения в нагрузке наибольшей мощности.

Режим холостого хода возникает при отключении нагрузки, при обрывах цепи (). Режим короткого замыкания – при .

 

4.5. Воздействие, реакция, параметры и характеристики цепей

Большинство электрических цепей служат средствами связи для передачи сигналов от источника сигнала в нагрузку (рис. 4.20).

 

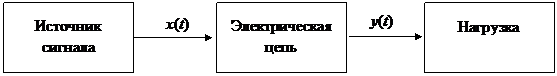Рис. 4.20

 

Сигнал источника сигнала x (t) на входе цепи называется входным сигналом или воздействием.

Сигнал на выходе цепи y (t) называется выходным сигналом, откликом или реакцией цепи. В общем случае связь между откликом и воздействием представляет собой дифференциальное уравнение y (t) = F (x (t), a, b, c,...), где a, b, c … – параметры элементов, входящих в электрическую цепь.

Если входной сигнал гармонический и характеризуется комплексной амплитудой 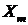и цепь линейна, то откликом будет являться также гармонический сигнал с комплексной амплитудой . При этом связь между комплексными амплитудам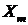и и имеет вид линейного алгебраического уравнения

,

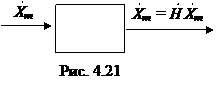
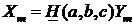где 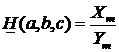– параметр электрической цепи (рис. 4.21).

Поскольку в состав цепей входят элементы, сопротивления которых зависят от частоты, то параметры цепей оказываются зависящими от частоты. Зависимость параметров цепи от частоты называют частотными характеристиками, или частичными функциями параметров цепи.

 

 

4.6. Основные свойства линейных цепей

Свойство 1. В линейных цепях выполняется принцип суперпозиций, т.е. отклик линейной цепи на сумму воздействий равен сумме откликов на действие каждого воздействия в отдельности. Рассмотрим линейную цепь (рис. 4.21).

Если x(t) = x ₁,то y = y ₁ = kx ₁;

если x(t) = x ₂, то y = y ₂ = kx ₂;

если x(t) = x ₁ +x ₂,то y = kx ₁ +kx ₁ = y ₁ +y _2.

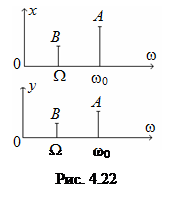
Свойство 2. В линейных цепях новых гармонических составляющих не возникает.

Рассмотрим линейную цепь вида у = kх. Пусть x (t) = A cos ω₀ t + B cos Ω t, тогда у (t) = kA cos ω₀ t + kB cos Ω t (рис. 4.22).

 

4.7. Основные свойства нелинейных цепей

Свойство 1. В нелинейных цепях принцип суперпозиции не выполняется. В качестве примера нелинейной цепи рассмотрим y = kx ² (рис. 4.23).

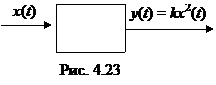Если x (t) = x ₁, то y = y ₁ = kx ₁²;

если x (t) = x ₂,то y = y ₂ = kx ₂²;

если x(t) = x ₁ + x ₁, то y = kx ₂² + kx ₂² + 2 kx ₁ x ₂.

Слагаемое 2 kx ₁ x ₂ возникает в результате взаимодействия двух сигналов в нелинейной цепи. Его называют комбинационной составляющей.

Свойство 2. В нелинейных цепях происходит трансформация спектра, т.е. появляются новые гармонические составляющие.

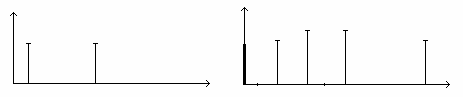
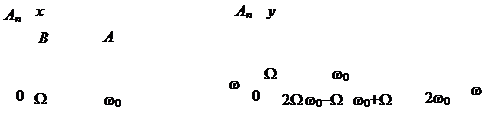На рис. 4.24 показаны спектры сигналов на входе и выходе цепи.

а б

Рис. 4.24. Спектры сигналов: а – на входе, б – на выходе цепи

4.8. Основные задачи теории электрических цепей

Основных задач две.

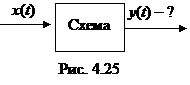1) Задача анализа электрической цепи состоит в отыскании откликов y_i (t), т.е. токов и напряжений на интересующих нас участках цепи по заданной схеме и воздействиям x_j (t). Схематично задача анализа показана на рис. 4.25.

Задача анализа имеет единственное решение (она однозначна).

2) Задача синтеза электрической цепи состоит в отыскании схемы цепи (структуры цепи) и параметров ее элементов по заданным откликам и воздействиям. Схематично задача синтеза показана на рис. 4.26.

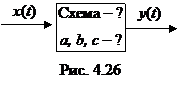Задача синтеза сложнее задачи анализа и обычно неоднозначна, т.е. можно создать ряд схем с одной и той же функцией цепи. Окончательный вариант схемы выбирается на основе дополнительных требований к ней.

Например:

1) Синтезировать схему при минимальной стоимости ее деталей;

2) синтезировать пассивную схему, используя только элементы R и C.

 

4.9. Методы анализа (расчета) линейных цепей
при гармоническом воздействии

в общем случае расчет (анализ) электрических цепей сводится к отысканию токов во всех ветвях схемы. При гармоническом воздействии в основу всех методов расчета линейных цепей положен метод комплексных амплитуд (МКА). Возможность применения МКА основана на том, что в линейных цепях новых гармонических составляющих не возникает, а потому расчет цепей сводится к расчету амплитуд и начальных фаз токов или напряжений на интересующих нас участках цепи, в то время как частота в любой точке цепи равна частоте входного сигнала.

Метод комплексных амплитуд состоит в следующем:

1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:

а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.

б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е. х (t) = X_m cos(w₀ t – j _x) ® X_m = X_m e^{–j j x}.

Z L=j w L

L

Z C= 1/(j w C)

C

Z R=R

R

Рис. 4.27

2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е. Y_m = Y_m e^{–j j y}.

3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.

Y_m = Y_m e ^{–j j y} ® y (t) = Y_m cos(w₀ t – j _y).

Основными методами анализа (расчета) являются:

1. Метод токов ветвей (МТВ).

2. Метод контурных токов (МКТ).

3. Метод узловых потенциалов (МУП).

4. Метод наложения.

Название метода дается в соответствии с тем, какая величина при составлении уравнений состояния принимается за неизвестную в данном методе расчета. Рассмотрим подробнее эти методы.

 

4.9.1. Метод токов ветвей (МТВ)

Данный метод основан на применении 1-го и 2-го законов Кирхгофа. За неизвестные величины в этом методе принимаются искомые токи во всех ветвях схемы. Для того чтобы задача имела однозначное решение для схемы, состоящей из b ветвей (b = N), необходимо составить N независимых уравнений.

Порядок решения данным методом.

1) Проводится топологический анализ схемы.

а) Во всех ветвях стрелками показывают положительное направление токов и нумеруют их I ₁, I ₂, …, I_N. Отсюда определяют число ветвей b = N.

б) Подсчитывают число узлов у и определяют число независимых узлов N_у = у – 1.

в) Подсчитывают число независимых контуров по формуле
N_k = b – у + 1. На схеме независимые контуры выделяют дугами. Стрелкой на дуге показывают положительное направление обходов элементов контуров. Эти контуры нумеруют. За положительное направление принимают направление по часовой стрелке.

2) По 1-му и 2-му законам Кирхгофа относительно токов ветвей записывают уравнения. Общее число уравнений составляет N_y + N_k = b, это означает, что записанная система относительно токов ветвей имеет однозначное решение. В общем случае для схемы из b = N ветвей составленные уравнения образуют систему линейных алгебраических уравнений N -го порядка:

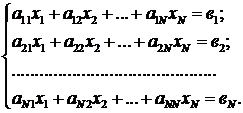
где x_i – искомые токи ветвей; a_ji – постоянные коэффициенты, зависящие от параметров пассивных элементов схемы; в_i – постоянные величины, зависящие от параметров активных элементов схемы.

3) Токи в ветвях находят по правилу Крамера

x_i= ; ,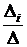

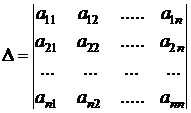где D – главный определитель системы; D _i – определитель, получается из главного D путем замены i -го столбца на столбец свободных членов в_i.

Пример. Дана комплексная схема замещения электрической цепи (рис. 4.28). Определить токи во всех ветвях схемы.

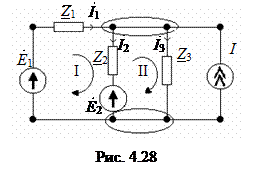1) Проведем топологический анализ.

а) b = 3; б) y = 2, N_у =1; в) N_k = b – y + 1 = 2.

2. Запишем систему уравнений, составленную по методу токов ветвей.

I ₁ – I ₂ – I₃ = – I для узла 1;

Z ₁ I ₁ + Z ₂ I ₂ + 0 I ₃ = E ₁ – E ₂для контура 1;

0 I ₁ + Z ₂ I ₂ + Z ₃ I ₃ = E ₂ для контура 2.

 

4.9.2. Метод контурных токов (МКТ)

Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.

Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).

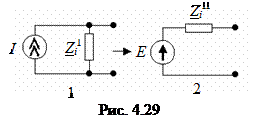Эта схема эквивалентна, если

а) E = I Z _i ^I;

б) Z_i ^II = Z_i ^I.

1) Топологический анализ схемы.

а) Как и в предыдущем методе, определяют число ветвей b.

б) Определяют число узлов у.

в) Подсчитывают число независимых контуров N_k = b – y + 1.

Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.

Все контуры нумеруют и каждому контуру присваивают свой контурный ток: I_{k 1}; I_{k 2}; I_kNk.

За положительное направление контурного тока принимают положительное направление обхода контура.

2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений N_k = N_k порядка:

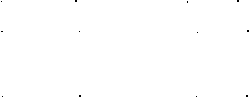
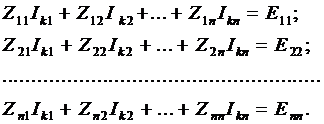
где I_ki – контурный ток i -го контура;

Z_ii – собственное сопротивление i -го контура и равно алгебраической сумме сопротивлений, входящих в i -й контур;

Z_ji – сопротивление смежных ветвей между i -м и j -м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;

E_ki – контурная ЭДС i -й ветви. Она равна алгебраической сумме ЭДС, входящих в i -й контур. Контурная ЭДС E_ki берется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.

3) По правилу Крамера находят контурные токи I_ki= .

4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. Если токи оказались положительными, то выбранное направление совпадает с истинным и наоборот.

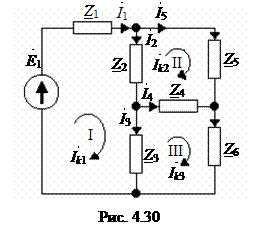
Пример. Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.

Проводим топологический анализ

а) b = 6; б) y = 4; в) N_k = 6 – 4 + 1=3.

2) Составим систему уравнений по методу МКТ

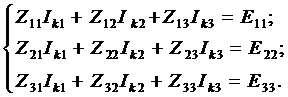
где

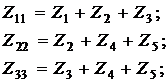
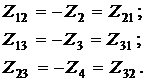
E ₁₁ = E ₁; E ₂₂ = 0; E ₃₃ = 0.

3) По методу Крамера находим контурные токи I_ki = .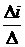

4) Находим токи в ветвях: I ₁ = I_{k 1}; I ₂ =
= I_{k 1} – I_{k 2}; I ₃ = I_{k 1} – I_{k 3}; I ₄ = – I_{k 2} + I_{k 3}; I ₅ = I_{k 2}; I ₆ = I_{k 3}.

4.9.3. Метод узловых потенциалов (МУП)

Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.

Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).

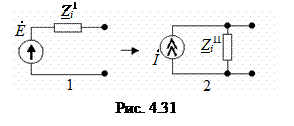а) I = E / Z_i ^I;

б) Z_i ^II = Z_i ^I.

1) Топологический анализ.

а) Подсчитывают число ветвей b и число узлов y. Определяется количество независимых узлов N_y = y – 1.

б) Нумеруют все узлы. Один из узлов, к которому сходится наибольшее число ветвей, считают нулевым, где 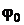– потенциал нулевого узла.

2) По 1-му закону Кирхгофа составляют уравнения для N узлов схемы и решают их относительно потенциалов узлов:

,

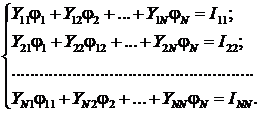где Y_ii – собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся в i -м узле, все они берутся со знаком «+»;

Y_ij – межузловая проводимость между i -м и j -м узлами. Проводимости всех узлов берутся со знаком «–»;

I_ii – алгебраическая сумма токов источников тока, сходящихся в i -м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».

3) Потенциалы узлов находят по формуле Крамера

.

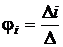4) Токи в ветвях находят по закону Ома

I = (j₁ – j₂)/ Z.

Пример. Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.

Z 2

I 2

Предварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33).

Z 4

Z 3

Z 1

I 1

I 3

I

I

I 4

I 2

I 1

E 2

E 1

Z 4

Z 3

Z 2

Z 1

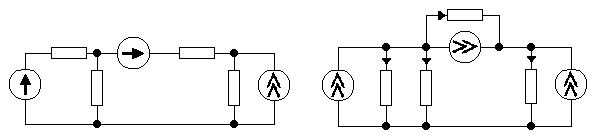
Рис. 4.32 Рис. 4.33

 

Проведем топологический анализ.

а) число ветвей b = 4 с токами: ;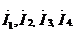

б) число независимых узлов N_у = 2, их потенциалы: φ₁ и φ₂ (рис. 4.33).

Составим систему уравнений по методу узловых потенциалов:

;

.

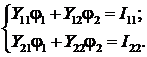
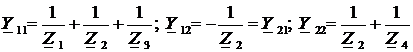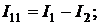
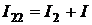По методу Крамера найдем потенциалы узлов: .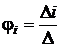

По закону Ома найдем токи во всех ветвях схемы:

.

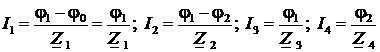Контрольные вопросы

1. каковы основные свойства линейных цепей?

2. Какие узлы и контуры называются независимыми?

3. Записать закон Ома в комплексной форме.

4. На каком законе основаны методы контурных токов и узловых потенциалов.

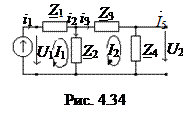
5. Записать уравнения по методу контурных токов для схемы на рис. 4.34.

6. 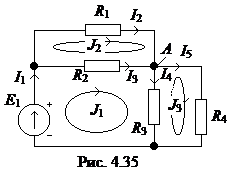Записать уравнение по методу узловых потенциалов для узла А схемы на рис. 4.35.

7. Записать второй закон Кирхгофа (для контура J ₁ на рис. 4.35).

8. Записать уравнение по методу узловых потенциалов для узла А схемы на рис. 4.35.

9. Записать уравнения по методу контурных токов для схемы на рис. 4.35.

10. Для независимых узлов схемы на рис. 4.35 записать уравнения по 1-му закону Кирхгофа.

a) I 1 – I 2 – I 3 = 0 I 2 + I 3 – I 4 – I 5 = 0 I 4 + I 5 – I 1 = 0	б) I 1 – I 2 – I 3 = 0 I 2 + I 3 – I 4 – I 5 = 0
в) I 1 + I 2 – I 3 = 0 I 2 + I 3 – I 4 – I 5 = 0 I 4 + I 5 – I 1 = 0	г) I 1 + I 2 + I 3 = 0 I 2 + I 3 – I 4 – I 5 = 0