ЗАНЯТИЕ 11. Предельные теоремы теории вероятностей
Цель занятия: изучение законов больших чисел и центральной предельной теоремы.
Краткие теоретические сведения: законы больших чисел и центральная предельная теорема.
Ряд утверждений и теорем в теории вероятностей объединены общим названием: законы больших чисел.
Понятие сходимости по вероятности.
Последовательность случайных величин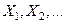 
сходится к случайной величине Х по вероятности при n® 
(обозначение: 
), если для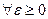 
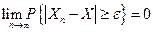(или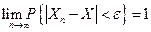 
).
Замечание. В частных случаях в качестве предельной величины может выступать и не случайная величина (например M [ X ]).
Пример 1. Рассмотрим следующую последовательность случайных величин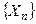 
, где закон распределения Хn описывается таблицей
| 
| |
| 
| 
|
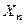
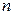
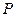
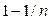
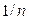
a) Показать, что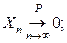 
б) Можно ли утверждать, что последовательность реализаций данной случайной последовательности сходится к 0в обычном смысле?
а) В силу неотрицательности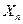 
имеем следующую цепочку равенств:
.
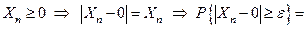
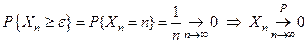Таким образом, утверждение в пункте а) доказано.
б) Пусть эксперимент проведен и реализовалась последовательность x1, x2,…, xn, где каждое xn Î {0 ,n } Þ на n- ом месте этой последовательности при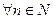 
может оказаться число n (поскольку вероятность этого события ненулевая) Þ ни одна из сколь угодно малых окрестностей точки x= 0 не может считаться "ловушкой" для последовательности { xn }. Таким образом,нельзя считать, что последовательность реализаций сходится к нулю в обычном смысле. 
Теорема 1 (закон больших чисел в формулировке Чебышева).
Пусть для последовательности { Xn }выполняются следующие условия:
а)Элементы последовательности попарно независимы;
б)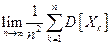 
=0.
Тогда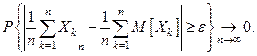 
Замечание. Теорема Чебышева остается верной, если заменить попарную независимость на попарную некоррелированность.
Теорема 2. (Закон больших чисел в формулировке Бернулли.
Пусть Xn - число успехов в n опытах по схеме Бернулли с вероятностью p успеха в одном опыте, т.е. Xn~B(n,p).
Тогда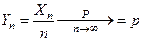 
, т.е. относительная частота успехов 
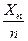сходится по вероятности к вероятности p успеха в одном опыте. Это утверждение является обоснованием статистического подхода к вероятности.
Пример 2. (сборка точных механизмов). Пусть 
- случайная длина детали, сходящей с конвейера. Известны ее основные характеристики:
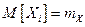=10 см, 
= 
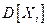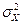=0,04 см2
Относительную точность изготовления детали можно характеризовать отношением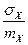 
. Производится сборка 9 подобных деталей (т.е. их длины складываются). Обозначим 
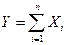. Вычислить относительную точность для Y, т.е. отношение 
.
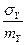◄Считая, что длина каждой изготовленной детали не зависит от остальных и используя свойства операторов математического ожидания и дисперсии, получаем:
.
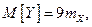
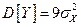Отсюда следует: =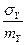 
. Таким образом, относительная точность собранной детали повысилась в 3 раза. ►
Из рассмотренных примеров можно сделать следующий вывод: проявление закона больших чисел связано главным образом с тем, что сумма конечного числа независимых случайных слагаемых имеет меньший относительный разброс, измеряемый отношением среднего квадратического отклонения к математическому ожиданию, чем у отдельно взятого слагаемого.
Теорема 3. (Центральная предельная теорема в формулировке. Ляпунова).
Пусть для последовательности случайных величин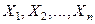 
выполняются условия:
а) они независимы;
б) они одинаково распределены;
в) существуют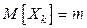 
и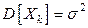 
.
Обозначим: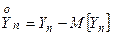 
, 
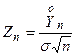, где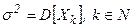 
.
Тогда 
для случайной величины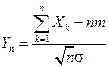 
справедливо предельное соотношение 
, 
, где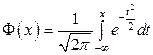 
- функция Лапласа, т.е. закон распределения величины 
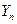приближантся к стандартному нормальному закону 
.
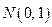Замечание 1. Мы дали одну из простейших формулировок центральной предельной теоремы. Все более поздние формулировки связаны с устранением пункта б), но тогда усложняется условие в). Чаще всего оно формулируется в виде условия Линдеберга (гарантирует, что все слагаемые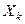 
вносят равномерно малый вклад в общую дисперсию).
Замечание 2. С учетом замечания 1 смысл центральной предельной теоремы состоит в том, что при суммировании большого числа независимых случайных факторов 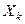результат суммирования имеет закон распределения, близкий к нормальному, т.е. при 
приближенно можно считать: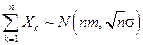 
.
Центральная предельная теорема играет большую роль в приложениях теории вероятностей. Одним из ярких примеров применения этой теоремы на практике является баллистика, изучающая явления рассеивания снарядов при стрельбе по цели.
На траекторию полета снаряда действует множество независимых факторов: колебания атмосферного давления, влажности, температуры, отклонения величины заряда и веса снаряда от номинала, ошибка прицеливания, сила ветра на различных высотах и т.д. Результатом этих многочисленных воздействий, каждое из которых вносит свой равномерно малый вклад в общую сумму (ограниченность дисперсий!) является то, что отклонение точки попадания от цели удивительно точно описывается двумерным нормальным законом распределения.
Другим примером применения центральной предельной теоремы является теория и практика измерений. Всякое измерение неизбежно сопряжено с погрешностями. Реально наблюдаемая погрешность измерения является суммой элементарных погрешностей, вызванных многочисленными факторами, каждый из которых лишь незначительно влияет на результат. В силу центральной предельной теоремы результирующая погрешность должна быть приближенно нормальной. Это обстоятельство играет решающую роль в разработке эффективных методов обработки опытных данных в математической статистике.
Задачи для решения на занятиях:
Л-2, №№18.543, 18.544, 18.561, 18.562, 18.563, 18.565, 18.420.
Задачи на дом:
Л-2,№№ 18.246, 18.554, 18.564, 18.566, 18.567.