ЗАНЯТИЕ 9. Нормальный и пуассоновский законы распределения
Цель занятия: изучение важнейших законов распределения – пуассоновского и нормального.
Краткие теоретические сведения: законы Пуассона и Гаусса.
Распределение Пуассона
СВДТ Х имеет распределение Пуассона с параметром 
, если ее возможные значения (реализации) 
, где 
(счетное множество значений), а соответствующие им вероятности выражаются формулой: 
.
Замечание. Это распределение зависит от одного параметра a, поэтому пишут 
. Важнейшие числовые характеристики : 
, 
, 
.
Вывод. Параметр a в распределении Пуассона является одновременно математическим ожиданием и дисперсией.
Теорема (Пуассон). Если 
и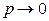 
так, что 
, то для любого фиксированного значения m ()
.
Комментарий. Из теоремы Пуассона следует, что распределение Пуассона является предельным для биноминального распределения, когда число опытов n неограниченно увеличивается () и одновременно параметр p (вероятность «успеха» в одном опыте) неограниченно уменьшается (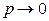), но так, что их произведение 
сохраняется в пределе постоянным и равным a, т.е. (на практике 
). Значит, распределение Пуассона с параметром 
можно применять для приближенных вычислений вместо биномиального, когда число опытов n очень велико, а вероятность p «успеха» в отдельном опыте очень мала, т.е. в каждом отдельном опыте «успех» приходит редко. Поэтому закон Пуассона в литературе часто называется «законом редких явлений».
Пример 1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодные изделия.
Решение. 
, 
, 
. Тогда 
, следовательно, 
. 
Замечание. Имеются специальные таблицы, с помощью которых можно найти 
, зная m и a.
Пример 2. В стае 1000 птиц, из которых 50 окольцованных. Орнитологами поймано 100 птиц. Каково среднее число окольцованных птиц среди пойманных? Какова вероятность того, что среди пойманных птиц нет окольцованных?
Решение. Орнитологами произведено 
независимых «опытов» (под «опытом» понимается поимка одной птицы из стаи) с одинаковой вероятностью «успеха» (под «успехом» понимается поимка окольцованной птицы) 
. Поскольку n достаточно велико, p – мала, а произведение 
удовлетворяет условию , то можно считать, что случайная величина X – количество окольцованных птиц среди пойманных – распределена по закону Пуассона. Тогда среднее число окольцованных птиц среди пойманных, т.е. математическое ожидание 
, равно 5 (в распределении Пуассона ). Далее 
.
Нормальное распределение
СВНТ Х имеет нормальное (гауссовское) распределение с параметрами 
и 
, если плотность вероятности имеет вид
, 
.
Замечание. Это распределение зависит от двух параметров – m и s, поэтому пишут 
.
Методами математического анализа можно легко построить график плотности вероятности 
(кривой Гаусса) (рис. 1):
Легко установить влияние параметров m и 
на вид кривой . Изменение m равносильно сдвигу кривой вдоль оси Ox. Причем в точке 
имеется единственный максимум функции , равный 
. Изменение равносильно изменению масштаба кривой по обеим осям (например, при удвоении масштаб по оси Ox удвоится, а по оси Oy – уменьшится в два раза, при этом площадь под графиком всегда равна единице) (рис. 2).
Общим называется нормальное распределение с параметрами m и s. Если случайная величина 
, то она называется стандартизованной нормальной случайной величиной. Ее плотность:
. Эта функция табулирована только для 
, поскольку является четной, т.е. 
.
Математическое ожидание, дисперсия и среднее квадратическое отклонение равны: 
, 
, 
.
Таким образом, смысл параметров m и случайной величины следующий: 
.
Замечание. Поскольку график функции плотности случайной величины симметричен относительно прямой , то ответ можно было получить сразу. Кроме того, мода и медиана случайной величины совпадают с ее математическим ожиданием и равны m.
Функция распределения стандартизованной нормальной случайной величины имеет вид: 
.
Она часто называется функцией нормального распределения и также табулирована для , поскольку 
.
Кроме того, в этой таблице приведены значения функции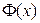 
лишь для 
. Это обусловлено тем, что при 
значения функции 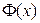практически не отличается от единицы. Поэтому при решении задач можно считать, что 
для .
Функция распределения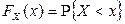 
для случайной величины связана функцией нормального распределения 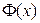при помощи формулы:
. Поэтому очевидно, что
.
Пример 3. Дана случайная величина 
. Найти 
.
Решение. 
.
Часто требуется вычислить вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине меньше заданного положительного числа e, т.е. требуется найти вероятность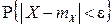 
. Задача решается так:
.
Случайная величина с большой вероятностью принимает значения, близкие к своему математическому ожиданию, что описывается «правилом k сигм»:
Пример 4. Рост взрослого мужчины удовлетворительно описывается нормальным законом распределения. По статистике средний рост составляет 180 см, а среднеквадратическое отклонение равно 7 см. Найти вероятность того, что рост наугад взятого мужчины будет отличаться от среднего роста менее чем на 7 см.
Решение. Обозначим рост наугад взятого взрослого мужчины через X. По условию задачи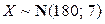 
. Требуется найти 
. Тогда
.
Пример 3. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина детали 40 см и среднее квадратическое отклонение равно 0,4 см, то какую точность длины изделия можно гарантировать с вероятностью 0,8?
Решение. По условию задачи случайная величина X – длина изготавливаемой детали – имеет нормальное распределение 
. Требуется найти положительное число 
, для которого 
. Поскольку 
, то задача сводится к решению неравенства 
. По таблице квантилей нормального распределения 
находим: 
, или 
. Таким образом, наименьшее значение равно 0,5128 см.
Задачи для решения на занятиях:
Л-2, №№18.352, 18.353, 18.356, 18.362, 18.364, 18.365.
Задачи на дом:
Л-2,№№ 18.354, 18.357, 18.363, 18.366, 18.367, 18.368.