ТЕМА 1. СКАЛЯРНЫЕ НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
Задание 1
Исследовать скорость сходимости (требуемое количество итераций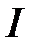 
) метода а) дихотомии и хорд; б) Ньютона; в) секущих и г) простых итераций для численного решения уравнения Кеплера 
с точностью до 
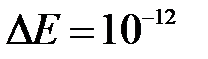в зависимости от параметров уравнения 
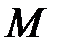и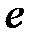 
на сетке 
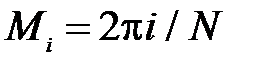и 
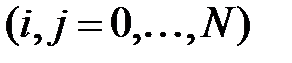. Представить результаты графически как поверхность (или карту линий уровней) зависимости 
.
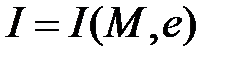Рекомендации: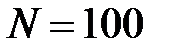 
; 
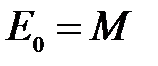(начальное приближение); для метода секущих 
.
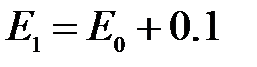Задание 2
С точностью до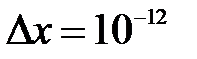 
методом I) дихотомии; II) секущих найти все корни многочлена а) Лежандра; б) Чебышева 
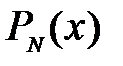степени 
на отрезке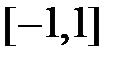 
. Многочлены задаются рекуррентно: для варианта а)
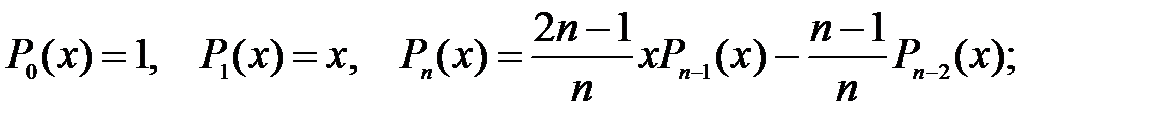
для варианта б)
Рассмотреть случаи 
. Сравнить (для варианта б) вычисленные корни полинома Чебышева с их точными значениями
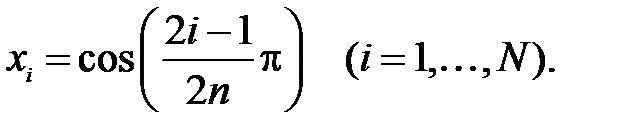
Рекомендации: I) для метода дихотомии выполнять поиск корней на начальных отрезках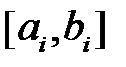 
c граничными значениям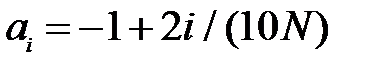и 
и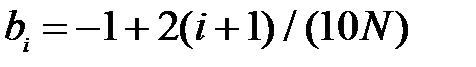 
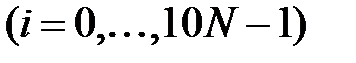; II) для метода секущих принимать начальные приближения 
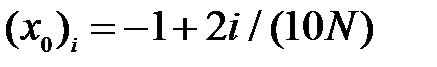и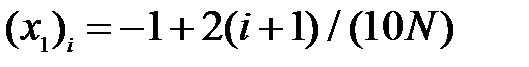 
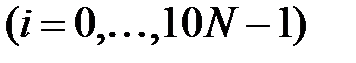; для каждой пары приближений найти соответствующий корень многочлена. Из всех найденных корней выбрать 
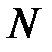различных.
Задание 3
Определить область сходимости метода Ньютона с точностью до 
к нулевому корню функции а)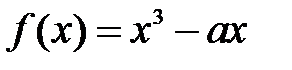 
; б)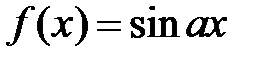 
(константы произвольные).
Рекомендации: рассмотреть начальные приближения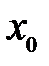 
на сетке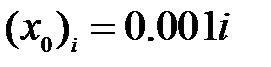 
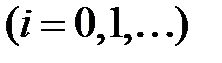; для каждого найти решение соответствующего уравнения; первое наименьшее из начальных приближений, для которого численное решение ненулевое, будет задавать правую границу искомой области сходимости метода к нулевому решению. Для определения левой границы выполнить то же самое на сетке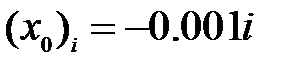 
.
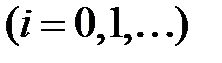Задание 4
Исследовать зависимость получаемого методом Ньютона численного решения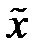 
уравнения а) 
; б)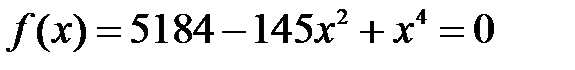 
, а также скорости сходимости (количество итераций 
) с точностью до 
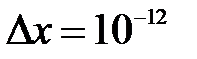от начального приближения 
Представить зависимост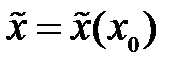и 
и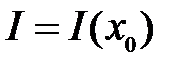 
графически.
ТЕМА 2. СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ И
СОБСТВЕННЫЕ ЗНАЧЕНИЯ
Задание 1
Программно реализовать метод Гаусса для численного решения систем линейных уравнений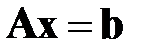 
произвольного порядка. Опробовать метод на примере системы уравнений четвертого порядка 
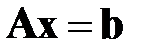, где
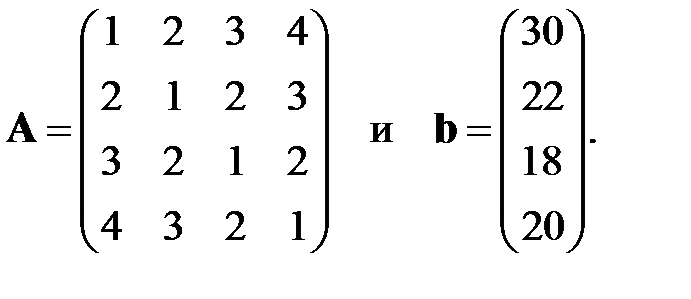
Сравнить численное решение с точным. Оценить вычислительные ошибки численного решения.
Задание 2
Программно реализовать метод Гаусса для вычисления определителя матрицы 
произвольного порядка. Опробовать метод на примере матрицы четвертого порядка
Сравнить численное решение с точным значением определителя. Оценить ошибку численного решения.
Задание 3
Программно реализовать метод Гаусса для вычисления обратной матрицы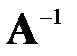 
произвольного порядка. Опробовать метод на примере матрицы четвертого порядка
Сравнить численно полученную обратную матрицу с точной
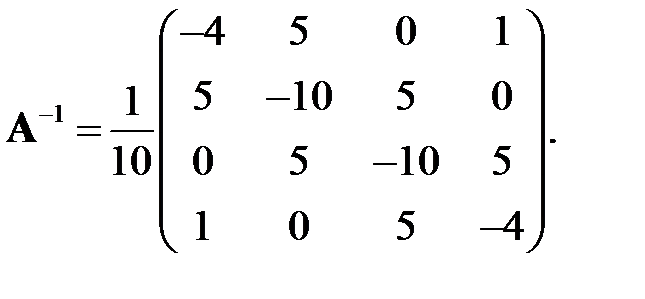
Оценить вычислительные ошибки численного обращения матрицы.
Задание 4
Программно реализовать метод простых итераций и метод Зейделя для численного решения систем линейных уравнений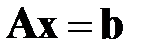 
произвольного порядка. Опробовать методы на примере системы уравнений четвертого порядка, где
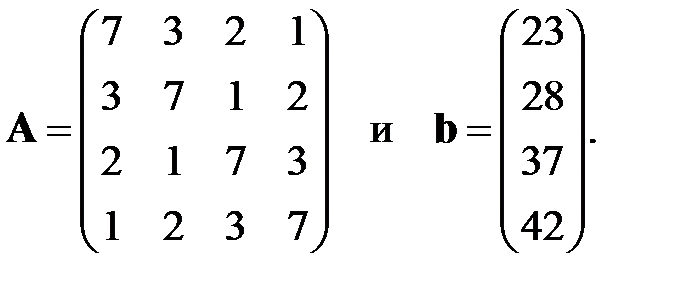
Сравнить скорость сходимости методов при достижении точности решения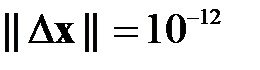 
. В качестве начального приближения выбирать нулевое 
.
Задание 5
Программно реализовать метод Зейделя для численного решения систем линейных уравнений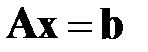 
произвольного порядка, где предполагается симметризация Гаусса: 
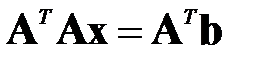. Опробовать метод на примере нормальной системы уравнений четвертого порядка, где
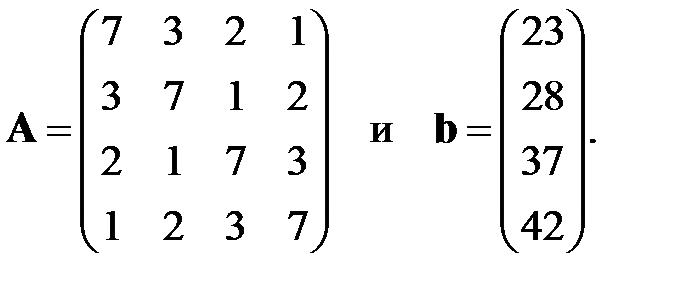
Сравнить скорость сходимости метода при достижении точности решения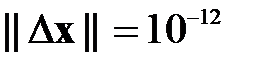 
с симметризацией и без. В качестве начального приближения выбирать нулевое 
.
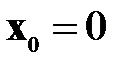Задание 6
Степенным методом определить максимальное собственное число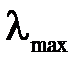 
и соответствующий собственный вектор 
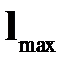для нормальных матриц
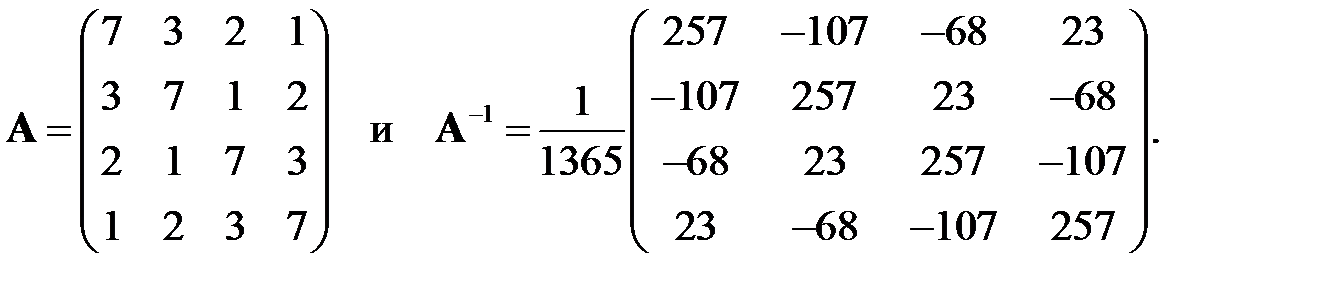
Решение находить с точностью до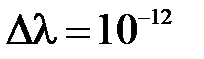 
. По количеству выполненных итераций оценить скорость сходимости метода. Вычислить число обусловленности матрицы как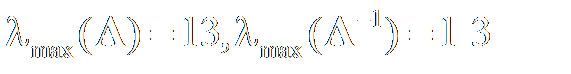 
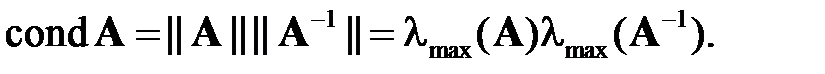
Задание 7
Программно реализовать метод вращений Якоби для вычисления собственных чисел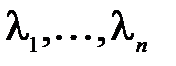 
. Решение находить с точностью до 
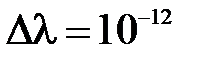. Опробовать метод на примере матрицы четвертого порядка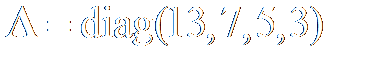 
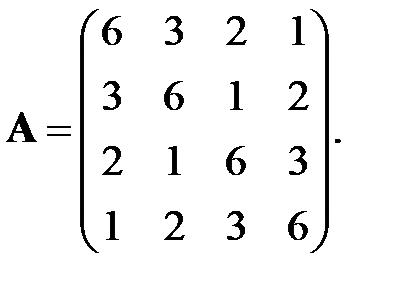
По количеству выполненных итераций оценить скорость сходимости метода. Вычислить число обусловленности матрицы.
Задание 8
Программно реализовать степенной метод для вычисления максимального собственного числа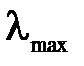 
(нормальной) матрицы произвольного порядка 
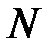с точностью до 
. Найти норму матрицы четвертого порядка
как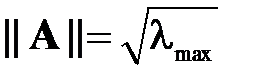 
, где 
― максимальное собственное число нормальной матрицы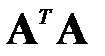 
. Вычислить норму иным способом, как
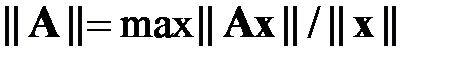
на множестве случайных векторов 
, равномерно распределенных внутри гиперкуба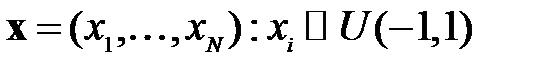 
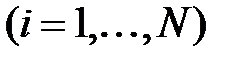. Выполнить 
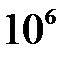испытаний. Сравнить численные значения норм.
Задание 9
Программно реализовать метод вращений Якоби для вычисления обратной нормальной матрицы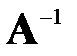 
произвольного порядка. Решение находить с точностью вычисления собственных чисел до 
. Опробовать метод на примере матрицы четвертого порядка
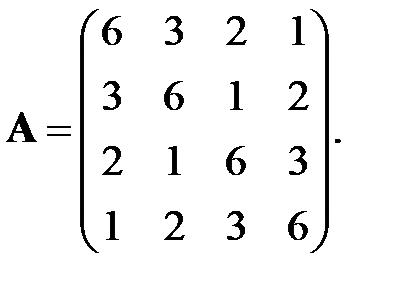
Сравнить численно полученную обратную матрицу с точной
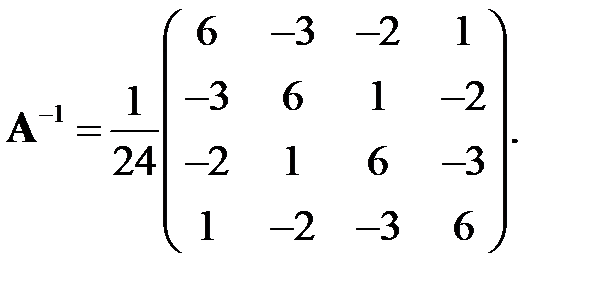
Оценить вычислительные ошибки численного обращения матрицы.
Задание 10
Исследовать скорость сходимости (количество итераций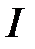 
) метода Зейделя при решении системы линейных уравнений второго порядка
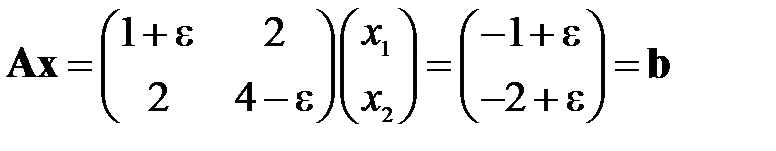
с точностью до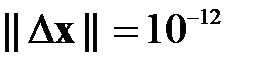 
. В качестве начального приближения выбирать нулевое 
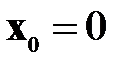. Рассмотреть варианты 
. Графически представить зависимость скорости сходимости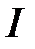 
от числа 
.
ТЕМА 3. АППРОКСИМАЦИЯ ФУНКЦИЙ
Задание 1
Составить программу для полиномиальной интерполяции 
функции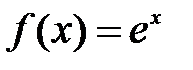 
по ее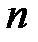 
узловым значениям на отрезке 
. Исследовать поведение ошибки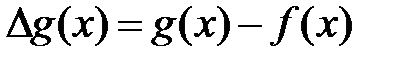 
на отрезке интерполяции при 
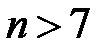для равномерной сетки: 
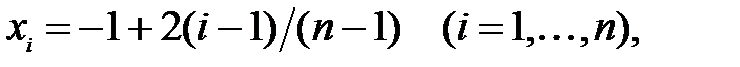и неравномерной сетки Чебышева:
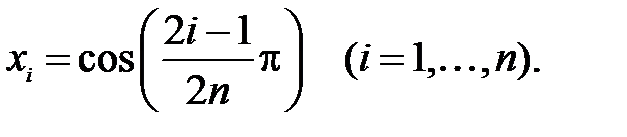
Варианты полинома 
: а) канонический; б) Лагранжа; в) Ньютона; г) Эйткена–Невилла.
Задание 2
Составить программу для вычисления первой производной от функции 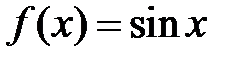I) 
и II)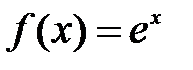 
, используя формулу дифференцирования интерполяционных многочленов: а) Лагранжа и б) канонического на равномерной сетке узлов: I) 
и II) 
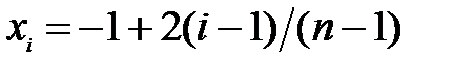
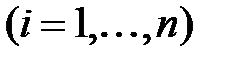, где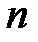 
― количество узлов. Представить графически зависимость ошибки вычисления производной 
от числа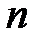 
.
Задание 3
Построить кубический сплайн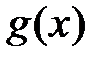 
для функции Рунге 
на равномерной сетке с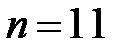 
узловыми значениями: 
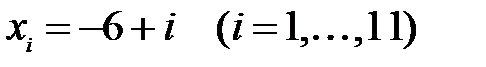. Оценить поведение ошибки 
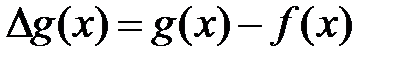внутри отрезка интерполяции 
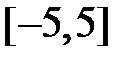. Представить результаты графически.
Задание 4
Используя узловые значения функции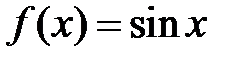 
на равномерной сетке 
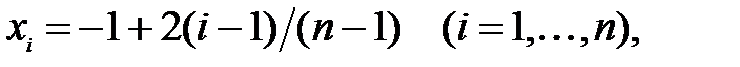методом наименьших квадратов построить аппроксимирующий канонический полином 
пятой степени. Вычислить среднеквадратическую ошибку полинома 
при 
. Сравнить коэффициенты полинома с коэффициентами ряда Тейлора для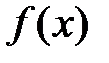 
.
Задание 5
Методом наименьших квадратов представить приближенно функцию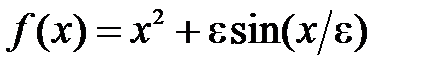 
квадратичной функцией 
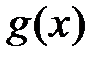, используя значения 
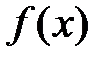на сетке узлов 
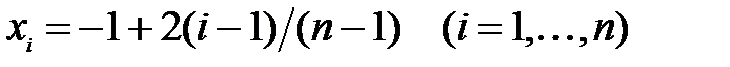при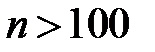 
. Представить аппроксимирующую функцию 
для случаев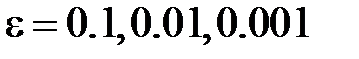 
и вычислить соответствующие среднеквадратические ошибки.
Задание 6
Методом наименьших квадратов представить приближенно функцию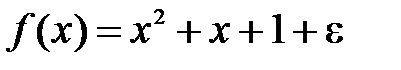 
квадратичной функцией 
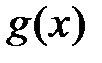, используя значения 
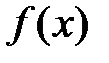на сетке узлов 
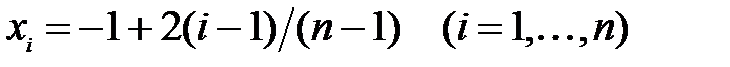. Здесь 
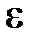— случайная величина, распределенная равномерно на отрезке 
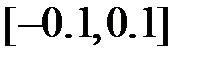. Показать, как зависит точность вычисления коэффициентов аппроксимации от количества измерений 
.