Рассмотрим зависимости объясняемой переменной 
от двух и более объясняющих переменных 
, 
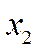,... Предполагается, что имеется 
наблюдений величины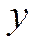 
и 
величин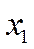 
, ,... 
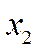, между которыми имеется связь вида
.
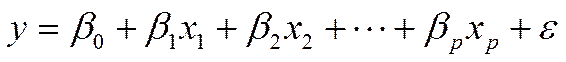Здесь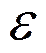 
случайная величина, распределенная по нормальному закону с нулевым средним и среднеквадратичным уклонением 
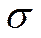. Будем считать, что коэффициент 
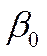стоит при переменной 
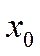, которая принимает все время одно и то же значение, равное 1.
Тогда результаты наблюдений могут быть записаны в виде 
–мерного вектор-столбца 
и матрицы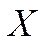 
размера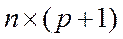 
.
В матрице 
каждый столбец представляет собой результаты наблюдений одной из величин , , ,...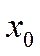 
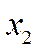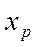. В предположении независимости наблюдений, можно показать, что статистической оценкой параметров 
, 
,…, 
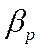, имеющей наименьшую дисперсию, является 
-мерный вектор
.
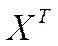– транспонированная матрица 
. Уравнение линейной множественной регрессии имеет вид
.
Раздельное влияние на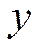 
объясняющих переменных характеризуется стандартизированными коэффициентами регрессии 
и коэффициентами эластичности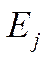 
(
).
, 
,
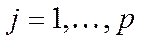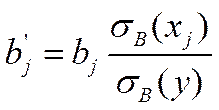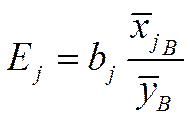где 
, 
, 
, 
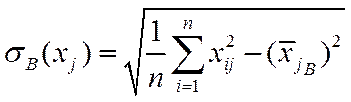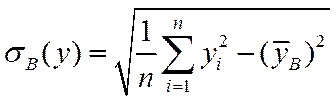. Стандартизированный коэффициент регрессии 
является статистическим аналогом коэффициента корреляции зависимой переменной 
с 
–й объясняющей переменной 
. Коэффициент корреляции принимает значения из отрезка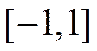 
. Равенство этого коэффициента 
указывает на функциональную зависимость между переменными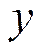 
, 
. Наоборот, близость коэффициента корреляции к нулю позволяет сделать заключение о слабой зависимости между 
и 
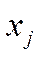. Коэффициент эластичности 
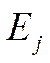показывает, насколько процентов изменится в среднем значение величины 
при увеличении только одной переменной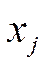 
на 1%.
Коэффициент детерминации регрессии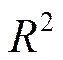 
определяется по формуле
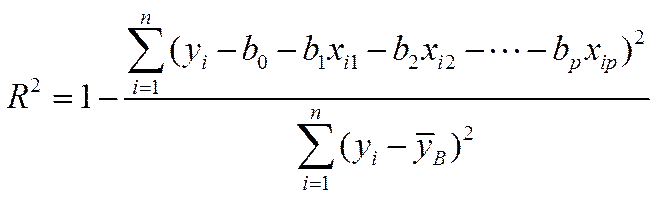
и показывает, какая доля в изменении зависимой переменной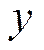 
обусловлена влиянием переменных 
, 
,... 
(
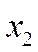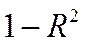, соответственно, показывает долю стохастической части 
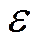в зависимости 
).
Зная коэффициент детерминации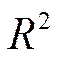 
, можно проверить гипотезу о значимости уравнения регрессии на заданном уровне значимости 
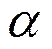. Гипотеза принимается, если выполнено неравенство
,
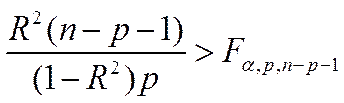где, как и раньше,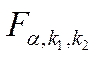 
– критическая точка распределения Фишера-Снедекора с вероятностью 
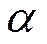и числом степеней свободы 
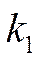и 
.
Задача. Имеются следующие данные о выработке литья на одного рабочего x 1 (т), браке литья x 2 (%) и себестоимости 1 т литья (т. руб.) по 10 литейным заводам:
| I | ||||||||||
| ||||||||||
| ||||||||||
| yi |
В предположениях классической линейной модели требуется:
1) найти множественный коэффициент детерминации и пояснить его смысл;
2) найти уравнение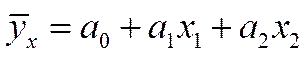 
множественной регрессии 
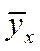на x 1, x 2, и оценить значимость этого уравнения и его коэффициентов на уровне a =0.05;
3) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизированные коэффициенты регрессии и коэффициенты эластичности;
Решение. По данным задачи выпишем вектор 
и матрицу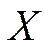 
, и определим коэффициенты уравнения линейной регрессии.
Тогда 
Найдем последовательно матрицу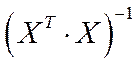 
и вектор 
. Имеем
откуда
и, кроме того, 
Теперь вычислим обратную матрицу:
.
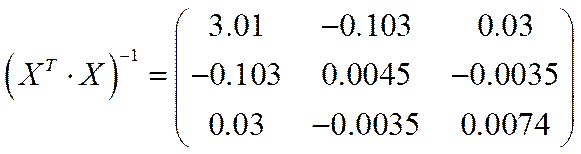Остается перемножить матрицу 
и вектор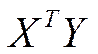 
:
Таким образом, уравнение регрессии имеет вид:
.
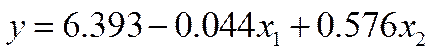Найдем точечные оценки для всех имеющихся переменных.
,
,
,
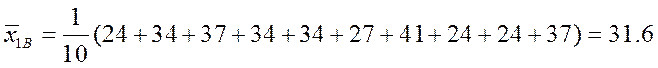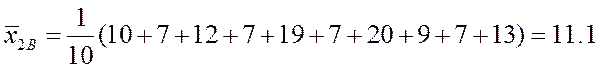Теперь мы в состоянии определить коэффициент детерминации уравнения регрессии
.
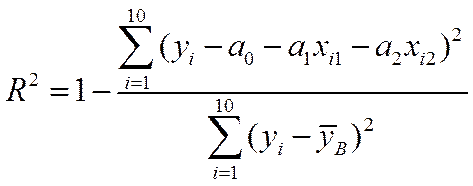Вычислим сначала сумму
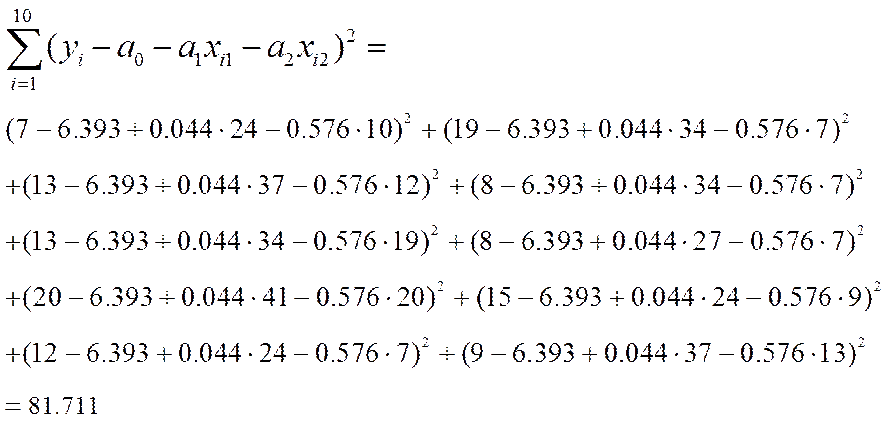
Отметим, что
,
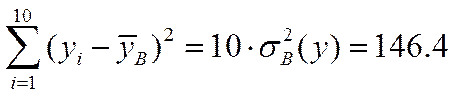откуда следует, что
Коэффициент детерминации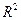 
интерпретируется как доля изменения зависимой переменной, обусловленная изменением независимых переменных, то есть в нашем случае изменение 
на 44.2% связано с изменением значений переменных 
и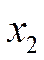 
и на 55.8% со случайными факторами.
Чтобы проверить гипотезу о значимости уравнения регрессии на уровне значимости 
, воспользуемся критерием значимости
.
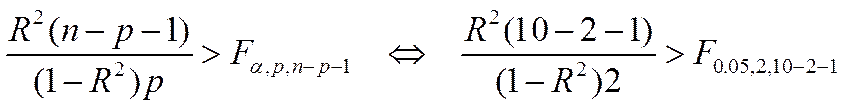В нашем случае
,
,
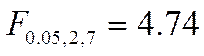и условие значимости не выполняется, что означает, что на выбранном уровне значимости гипотезы (когда мы хотим, чтобы вероятность ошибки первого рода была достаточно мала) экспериментальные данные позволяют считать, что на самом деле линейная часть уравнения регрессии равна нулю, и разброс значений переменной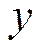 
связан только со случайными факторами.
Найдем стандартизированные регрессии и коэффициенты эластичности для каждой из объясняющих переменных. Имеем:
,
То, что выборочный коэффициент корреляции больше для переменной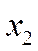 
указывает на то, что в нашем примере второй параметр более тесно связан с независимой переменной, чем первый. Далее,
,
,
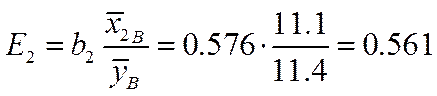откуда можно сделать вывод, что при увеличении величины 
на 1% величина 
уменьшается на 12.2%, в то время как увеличение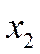 
на 1% дает прирост на 56.1%.