Рассматривается игра Г, в которой N – множество игроков. SÍN – некоторое подмножество (коалиция) всего множества игроков. S – коалиция действует как один игрок против остальных игроков, множество которых можно записать как N\S. Возможны формирования и нескольких коалиций SiÍN.
Определение. Функция υ(S), которая ставит в соответствие для коалиции S наибольший гарантированный выигрыш υ(S), называется характеристической функцией.
Следовательно функция υ(S) задаётся всех возможных коалиций, т.е. на множестве всех возможных подмножеств множества N, которое мы в дискретной математике называли булеаном множества N и обозначали как В(N) с мощностью этого множества 2|N|, указывающего на количество возможных подмножеств, включая пустое множество и само множество N. Так множество игроков N={1, 2, 3} имеет |В(3)|=23=8 подмножеств: В(3)= {Ø, {1},{2}, {3},{1,2}, {1,3}, {2,3}, {1, 2, 3}}
Пример 1. («Изобретатель»). Изобретатель создал новый инструмент для обработки приусадебных участков, но у него нет средств для организации производства этого инструмента. С этим вопросом он обратился к двум фирмам, специализирующимся по производству подобных инструментов. Прибыль при участии хотя бы одной из фирм в этом проекте оценивается в 5 млн. р., которой затем они должны поделиться с изобретателем. Необходимо определить характеристическую функцию данной игры.
Решение. Имеется три игрока: изобретатель и 2 фирмы, т.е.
N={1(изобретатель), 2(фирма 1), 3(фирма 2)},
Þυ(Æ)=υ({1})=υ({2})=υ({3})=υ({2,3})=0, так как здесь нет коалиций изобретателя с одной из фирм, υ({1,2})=υ({1,3})=υ({1,2,3})=5, так как здесь есть коалиции, обеспечивающие прибыль в 5 млн. р.
Пример 2. («Парковое строительство»). Городская служба имеет участок стоимостью 1 млн. р., на котором планирует разбить парк с развлечениями, но нет для этого средств. Служба может обратиться с этим вопросом к двум фирмам, специализирующимся на этом направлении, отчего стоимость участка возрастёт при участии 1-й фирмы до 1,5 млн. р., а при участии 2-й фирмы до 3 млн. р.
Необходимо определить характеристическую функцию данной игры.
Решение. Имеется три игрока: городская служба и 2 фирмы, т.е.
N={1(городская служба), 2(фирма 1), 3(фирма 2)}.
Þυ(Æ)=υ({2})=υ({3})=υ({2,3})=0, так как здесь нет коалиций городской службы с одной из фирм; υ({1})=1 – стоимость участка; υ({1,2})=1,5 как факт коалиции городской службы с первой фирмой согласно условию игры;
υ({1,3})= υ({1,2,3})=3, так как здесь есть коалиции, обеспечивающие прибыль в
3 млн. р., и не сказано про увеличение прибыли при участии 2-х фирм в проекте, что и соответствует наибольшему гарантированному выигрышу.
Далее для сокращения записи вместо полной записи типа υ({i}) будем писать υ(i).
Определение. Характеристическая функция υ(S), называется простой, если она принимает только два значения: 0 или 1.
Эта функция ведёт оценку игр с предпочтениями, когда важен факт предпочтения и неважна количественная оценка этого предпочтения.
Определение. Кооперативные игры, где все выплаты = 0 или 1, называются простыми.
Здесь имеет смысл только факт: коалиция выиграла (υ(S)=1) или коалиция проиграла (υ(S)=0).
Определение. Простая игра называется правильной, если υ(S)=1 - υ(N\S).
Из определения Þ коалиция выигрывает тогда и только тогда, когда игроки, не входящие в коалицию, проигрывают коалиции.
Примером простых игр есть голосование, когда победа коалиции назначается (принимается какое-то решение, согласно вопросу, поставленному на голосование) при достижении некоторого контрольного значения R>0.
Так в Совете безопасности ООН выигрывающими коалициями являются все постоянные члены ООН + ещё хотя бы один непостоянный член ООН.
В Верховной Раде Украины R=226>450/2.
Свойства характеристической функции.
1. Персональность: υ(Æ)=0, т.е. пустая коалиция не получит ничего.
2. Дополнительность: υ(S)+υ(N\S)=υ(N), т.е. сумма выигрышей коалиции и остальных игроков = сумма выигрышей всех игроков.
3. Неубываемость: из АÍВ Þ υ(А)£υ(В), т.е. у больших коалиций выигрыш не меньше, чем у меньших коалиций.
4. Супераддитивность: υ(S  L)³υ(S)+υ(L), если S, LÍN и S∩L=Æ, т.е. выигрыш объединённой коалиции будет не меньше, чем суммарный выигрыш отдельных коалиций, не имеющих общих игроков.
L)³υ(S)+υ(L), если S, LÍN и S∩L=Æ, т.е. выигрыш объединённой коалиции будет не меньше, чем суммарный выигрыш отдельных коалиций, не имеющих общих игроков.
Определение. Если υ(S  L)>υ(S)+υ(L), S, LÍ N и S∩L= Æ, то кооперативная игра называется существенной.
L)>υ(S)+υ(L), S, LÍ N и S∩L= Æ, то кооперативная игра называется существенной.
Определение. Если υ(S  L)=υ(S)+υ(L), S, LÍ N и S∩L= Æ, то кооперативная игра называется несущественной.
L)=υ(S)+υ(L), S, LÍ N и S∩L= Æ, то кооперативная игра называется несущественной.
Следовательно, для несущественной игры справедливо: 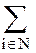 υ(i) = υ(N)
υ(i) = υ(N)
Определение. Кооперативная игра Г1с множеством игроков N и характерис-тической функцией υ1(S) называется эквивалентной игрой игре Г2с тем же множеством игроков N и характеристической функцией υ2(S), если
 (существуют) k>0 и вещественные сi (iÎN):
(существуют) k>0 и вещественные сi (iÎN):  υ2(S)= kυ1(S)+
υ2(S)= kυ1(S)+ 
Этот факт обозначается Г1~ Г2и говорит о том, что у эквивалентных игр характеристические функции отличаются только масштабом измерения и начальным значением.
Определение. Кооперативная игра называется нулевой, если " значения её характеристической функции равны 0, т.е. игроки не имеют заинтересованности.
Несложно сделать вывод о том, что " несущественная игра эквивалентна нулевой игре.
Определение. Кооперативная игра имеет (0,1)-редуцированную форму, если
"iÎN Þ υ(i)=0 и υ(N)=1.
Теорема 1. " существенная игра эквивалентна одной и только одной игре с (0,1)-редуцированной формой.
Решением игры с множеством игроков N является нахождение вектора 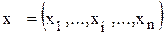 - вектора наград (выплат) с выполнением следующих двух условий:
- вектора наград (выплат) с выполнением следующих двух условий:
1. υ(N)= 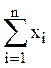 - групповое необходимое условие, т.е. сумма наград должна быть равна характеристической функции для коалиции из всех игроков
- групповое необходимое условие, т.е. сумма наград должна быть равна характеристической функции для коалиции из всех игроков
2.  ³ υ(i) - индивидуальное необходимое условие, т.е. награда не должна быть меньше его наибольшего гарантированного выигрыша.
³ υ(i) - индивидуальное необходимое условие, т.е. награда не должна быть меньше его наибольшего гарантированного выигрыша.
Определение. 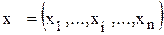 - вектор наград (выплат) при выполнении выше указанных двух условий называется обязательством или дележом.
- вектор наград (выплат) при выполнении выше указанных двух условий называется обязательством или дележом.
Рассмотрим разные варианты вектора наград х для примера 2(«Парковое строительство») для определения какой из вариантов является дележом, и какой нет.
| х | Делёж? | Причина |
| (1; 1; 1) | да | Выполняются оба условия |
| (0,7; 0,3; 0,2) | нет | Не выполняются оба условия |
| (1,5; 1,2; -0,1) | нет | Не выполняется условие 2) для 3-го игрока |
| (1,2; 1,2; 1,2) | нет | Не выполняется условие 1) |
Отметим следующие факты:
1. Для несущественной игры имеется только один делёж х={υ(1),…,υ(i),…,υ(n)}.
2. Для существенной игры имеется бесконечное множество дележей, которое можно представить в виде: х={υ(1)+α1,…,υ(i)+αi,…,υ(n)+αn}, где αi, ³0 (согласно свойству супераддитивности: υ(N) ³  υ(i))
υ(i))
К решению кооперативных игр существуют простые подходы и более сложные с привлечением различной сложности математического аппарата.
Простые подходы – решение в угрозах и контругрозах.
Идея данных подходов заключается в переговорных процессах между любыми игроками i и j, входящими в определённую коалицию S, о возможности их перехода в новую коалицию с возможностью улучшить свой выигрыш, т.е. цель переговоров: сделать коалиционное соглашение более устойчивым, отклонение от которого будет невыгодным.
Для улучшения устойчивости коалиций имеются и более строгие подходы, один из которых основан на идее доминирования дележей, приводящей, как и в бескоалиционных играх доминирование стратегий, к упрощению поиска решений.
Определение. Делёж х доминирует делёж у по коалиции S (обозначим  ), если: 1) " iÎ S Þ
), если: 1) " iÎ S Þ 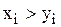 , т.е. делёж х лучше дележа у для всех членов коалиции;
, т.е. делёж х лучше дележа у для всех членов коалиции;
2)  υ(S) – реализуемость дележа х для коалиции (супераддитивность).
υ(S) – реализуемость дележа х для коалиции (супераддитивность).
Определение. Делёж х доминирует делёж у (обозначим 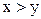 ), если:
), если:
 (существует) коалиция SÍ N, для которой
(существует) коалиция SÍ N, для которой  .
.
Отметим следующие факты: доминирование невозможно по: 1) одноэлементной коалиции и 2) коалиции из всех игроков. Приведём доказательство этих фактов:
1. Из определения  по условию 2) Þ
по условию 2) Þ 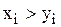
 υ(i), что противоречит условию 2) определения дележа, когда по доминированию имеем
υ(i), что противоречит условию 2) определения дележа, когда по доминированию имеем 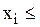 υ(i) Þ
υ(i) Þ  <υ(i), а по определению дележа необходимо:
<υ(i), а по определению дележа необходимо: 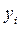 ³ υ(i).
³ υ(i).
2. Из определения 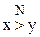 по условию 2) Þ
по условию 2) Þ 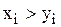 для "iÎNÞ
для "iÎNÞ  =υ(N),что противоречит условию 1) определения дележа, когда необходимо
=υ(N),что противоречит условию 1) определения дележа, когда необходимо 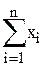 =υ(N)
=υ(N)
Эти факты говорят о том, что может и не быть доминирования дележей, и также может множество вариантов доминирования.
Пример 3. Дана игра с характеристической функцией:
υ(Æ)=υ({1})=υ({2})=υ({3})=0; υ({1,2})=0,1; υ({1,3})= υ({2,3})=0,2; υ({1,2,3})=1
Даны два дележа: х =(0,07; 0,86; 0,07) и у =(0,08; 0,80; 0,12)
Показать, что для коалиции S={1,3} 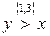 , т.е. делёж у доминирует делёж х по коалиции S.
, т.е. делёж у доминирует делёж х по коалиции S.
Решение. Самостоятельно убеждаемся, что х и у – дележи. Далее проверяем условие 1) определения:  =0,08>
=0,08>  =0.07;
=0.07;  =0,12>
=0,12> 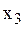 =0,.07Þ1) выполняется.
=0,.07Þ1) выполняется.
Проверяем условие 2) определения:  +
+  =0,2= υ({1,3})=0,2, так как нет превышения Þ2) выполняется Þ показали, что делёж у доминирует делёж х по коалиции S={1,3}.
=0,2= υ({1,3})=0,2, так как нет превышения Þ2) выполняется Þ показали, что делёж у доминирует делёж х по коалиции S={1,3}.
Цель оптимизации решений в кооперативных играх найти устойчивые дележи, отклонение от которых невыгодно игрокам.
Определение. Множество недоминируемых дележей называется ядром или С-ядром кооперативной игры, т.е. это решение которое нельзя улучшить никакими вариантами коалиций.
Это один из принципов оптимальности. Как и другие принципы оптимальности, описание которых будет дано несколько ниже, данный принцип имеет часто сложную реализацию, или неоднозначную, или нереализуем.
Для данного принципа приведём некоторые теоремы и выводы, которые помогут при поиске его реализации.
Из теоремы 1, выше сформулированной, для упрощения анализа существенные игры можно свести к (0,1)-редуцированной формой.
Теорема 2. Если υ1 и υ2 характеристические функции в эквивалентных играх Г1и Г2, и дележам  и
и  игры Г1соответствуют дележи
игры Г1соответствуют дележи  и
и 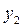 игры Г2, и если
игры Г2, и если  >(доминирует)
>(доминирует) 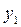 в игре Г1, то
в игре Г1, то  >
> 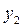 в игре Г2
в игре Г2
Теорема 3. В несущественной игре С-ядро состоит из единственного дележа этой игры (см. факт 2. после определения дележа).
Замечание. Для существенной игры С-ядро может быть Æ.
Достаточные условия не пустоты С-ядра были сформулированы О. Бондаревой (1963г.) и затем Л. Шепли (1967г.).
Теорема 4. Делёж хÎ С-ядру в том и только том случае, если для "SÍ NÞ  ³υ(S).
³υ(S).
Теорема 4 даёт метод оптимизации дележей: берём " делёж х и проверяем его согласно условиям теоремы на принадлежность С-ядру.
Пример 4. Возьмём произвольный вектор х=(х1, х2, х3) и применим к нему условия, которые делают его дележом согласно условий примера 1. («Изобретатель»):
Условие 1): х1+х2+х3=5; Условие 2): х1,х2,х3³0. Обозначим эти ограничения (1).
Для того, чтобы делёж хÎ С-ядру должны выполняться условия теоремы 4:
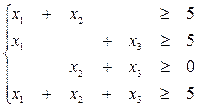 , обозначим эти условия (2).
, обозначим эти условия (2).
Из условия (2) следует необходимость выполнения следующего условия для существования непустого С-ядра: 2(х1+х2+х3)≥ υ({1,2})+ υ({1,3})+ υ({2,3}). (3)
Имеем 10=10, т.е. условие (3) выполнено, а знак равенства говорит о том, что С-ядро состоит из одной точки.
Из совместного выполнения условий (1) и (2) Þ
 , из чего Þ х2=х3=0, х1=5 Þ х=(5; 0; 0) есть С-ядро, которое состоит из одной точки. Это решение говорит о теоретической справедливости распределения дележа, указывая на особую важность в реализации проекта изобретателя. Поэтому на практике делёж будет справедливым, если большую часть прибыли получит именно изобретатель.
, из чего Þ х2=х3=0, х1=5 Þ х=(5; 0; 0) есть С-ядро, которое состоит из одной точки. Это решение говорит о теоретической справедливости распределения дележа, указывая на особую важность в реализации проекта изобретателя. Поэтому на практике делёж будет справедливым, если большую часть прибыли получит именно изобретатель.
Пример 5. Поступим как и в предыдущем примере: возьмём произвольный вектор х=(х1, х2, х3) и применим к нему условия, которые делают его дележом согласно условий примера 2. («Парковое строительство»):
Условие 1): х1+х2+х3=3; Условие 2): х1³1, х2,х3³0. Обозначим эти ограничения (1).
Для того, чтобы делёж хÎ С-ядру должны выполняться условия теоремы 4:
 , обозначим эти условия (2).
, обозначим эти условия (2).
Из условия (2) проверим необходимое условие (3) существования непустого С-ядра: 2(х1+х2+х3)≥ υ({1,2})+ υ({1,3})+ υ({2,3}). Имеем 6>4,5, где знак строгого неравенства говорит о том, что С-ядро состоит из множества точек.
Из совместного выполнения условий (1) и (2) Þ
 , из чего
, из чего
Þ х2=0, х1+х3=3, х1³1,5 и так как х3³0Þ 3³х1³1,5 Þ х=(х1; 0; 3-х1) есть С-ядро, состоящее из множества точек
По данному решению первая фирма не рассматривается как потенциальный игрок, вторая фирма покупает у городской службы участок по договорённости в интервале от 1,5 млн. р. до 3 млн. р. Þимеем множество вариантов решения.
Пример 5.(«Оркестр») Оркестр состоит из 3-х участников: (игрок 1-певец (S), игрок 2-пианист (Р), игрок 3-ударник (D)). Суммарный доход 3-х музыкантов при совместном выступлении =$10тыс. При вариантах выступления доход имеет следующие показатели: (S,P) =$8тыс.; (P,D) =$6.5тыс.; (S,D) =$5тыс.; (S) =$2тыс.;
(P) =$3тыс.; (D) =$0тыс. В каком составе музыкантам выгоднее выступать и как поделить деньги.
Проверим необходимое условие (3) существования непустого С-ядра: 2(х1+х2+х3)≥ υ({1,2})+ υ({1,3})+ υ({2,3}). Имеем 20 тыс.>19,5 тыс., где знак строгого неравенства говорит о том, что С-ядро состоит из множества точек.
Решение. х=(х1, х2, х3) – делёж. υ(1)=2; υ(2)=3; υ(3)=0; υ(1,2)=8; υ(1,3)=5; υ(2,3)=6,5; υ(1,2,3)=10. С-ядро данной игры: х1³2; х2³3; х3³0; х1+х2+х3=10; х1+х2 ³ 8; х2+х3 ³ 6,5; х1+х3 ³ 5. Имеем 3 граничных соотношения с учётом х1+х2+х3=10:
1. х1+х2 = 8 Þ х3=2; 2. х2+х3 = 6,5 Þ х1=3,5; 3. х1+х3 = 5 Þ х2=5;
Из соотношений 1. и 2. получим первую вершину С-ядра: (3,5; 4,5; 2).
Из соотношений 2. и 3. получим вторую вершину С-ядра: (3,5; 5; 1,5).
Из соотношений 1. и 3. получим третью вершину С-ядра: (3; 5; 2).
Следовательно, С-ядро есть множество решений, представляющее треугольник с найденными вершинами. Справедливым компромиссным решением для однозначности является центр данного треугольника: х* = (3,33; 4,83; 1,83).
 . Возможные двухэлементные коалиции дают дополнительныйвыигрыш:
. Возможные двухэлементные коалиции дают дополнительныйвыигрыш: 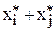 - υ(i,j)=0,16, когда общий делёж этих коалиций меньше 10. Следовательно, максимальная прибыль музыкантов 10 обеспечивается только при выступлениях втроём с оптимальным дележом дохода х* = (3,33; 4,83; 1,83).
- υ(i,j)=0,16, когда общий делёж этих коалиций меньше 10. Следовательно, максимальная прибыль музыкантов 10 обеспечивается только при выступлениях втроём с оптимальным дележом дохода х* = (3,33; 4,83; 1,83).
Другой принцип оптимальности дележей: нахождение n-ядра, когда обеспечивается минимальная степень неудовлетворённости дележом. Для формирования этого процесса вводится понятие эксцесса коалиции:
е(S,x)= υ(S) – x(S) – мера неудовлетворённости коалиции дележом x.
n-ядро представляет делёж, когда величина эксцесса минимизируется.
Теорема 5. n-ядро всегда существует и состоит из одного дележа, и если
С-ядро данной игры не пусто, n-ядро Î С-ядру.
Преимущества этого метода: 1) находится всегда один делёж; 2) его легко найти в Excel с помощью программы «Поиск решения» по следующей оптимизационной задаче:
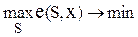 при ограничениях: Þ
при ограничениях: Þ 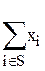 ³υ(S) и
³υ(S) и  =υ(N).
=υ(N).
n-ядро игры «Оркестр»: х* = (3,5; 4,75; 1,75) Î С-ядру данной игры, представляющего собой треугольник.
Третий принцип оптимальности дележей: нахождение решения по Нейману-Моргенштерну (или Н-М-решение) недостаточно хорошо разработан для применения на практике. Дадим лишь краткую идею метода: находится множество дележей не доминирующих друг друга, но которые в совокупности доминируют над всеми остальными дележами.
Четвёртый принцип оптимальности дележей предложен Ллойдом Шепли и, сегодня, является наиболее используемым на практике. Этот метод гарантирует существование и единственность решения любой кооперативной игры. Он базируется на принципе «справедливого дележа», исходя из вклада каждого игрока в выигрыш коалиции.
Определение. Вкладом i-го игрока называется величина υ(S)-υ(S\i), т.е. это приращение характеристической функции для коалиции S с игроком i и без него.
Определение. Вектор Шепли: Ф(υ)=(Ф1,…,Фn) – распределение выигрыша каждого игрока Фi, равное среднему вкладу i-го игрока в соответствующие коалиции S:  υ(S)-υ(S\i), (*)
υ(S)-υ(S\i), (*)
где  - Рn(k) вероятность появления k-элементных коалиций с игроком i, n – общее число игроков.
- Рn(k) вероятность появления k-элементных коалиций с игроком i, n – общее число игроков.
Аксиомы (свойства) Шепли.
1. Линейность: Ф(υ) – линейный оператор, т.е. для любых двух кооперативных игр с характеристическими функциями υ и w имеем:
Ф(υ+w) = Ф(υ) + Ф(w); и для " υ и для " числа α имеем: Ф(α υ)= α Ф(υ).
Это свойство говорит о том, что выигрыши в разных играх должны складываться
2. Симметричность: получаемый выигрыш не зависит от номера игрока.
3. Эффективность: «болван», игрок не приносящий пользы ни для одной коалиции имеет Фi=0, так как υ(S)-υ(S\i)=0.
Примечание: пример игры с «болваном»:
Три игрока имеют в игре следующую характеристическую функцию:
υ({1})=0; υ({2})=υ({3})=1; υ({1,2})= υ({1,3})=1; υ({2,3})=υ({1,2,3})=3
Здесь игрок 1 - «болван».
Теорема 6. Любаякооперативная игра имеет единственный делёж, удовлетворяю-щий аксиомам 1.-3., и это естьвектор Шепли.
Для простой игры, где выигрыш=1, а проигрыш=0 вектор Шепли выглядит так:
 (**)
(**)
Замечания: если вектор Шепли Î С-ядру, то этот делёж справедливый и устойчивый, если не Î С-ядру, то этот делёж справедливый, но может быть неустойчивым.
Пример 6. 4 акционера имеют следующее количество акций соответственно их нумерации: 10, 20, 30, 40, т.е. всего акций 100. Любое решение утверждается акционерами, имеющими в сумме более 50 акций. Найти делёж по вектору Шепли.
Решение: это простая игра, так как выигрыш (утвердить решение) = 1, а проигрыш (решение не утверждается) = 0, поэтому вектор Шепли будем вычислять по формуле (**):
Определим выигрывающие коалиции: (2,4), (3,4), (1,2,3), (1,2,4), (2,3,4), (1,3,4), (1,2,3,4).
1. Для нахождения Ф1 для игрока 1 найдём коалиции, выигрывающие с ним и не выигрывающие без него, чтобы иметь υ(S)-υ(S\1)=1-0=1, так как для остальных выигрывающих коалиций υ(S)-υ(S\1)=1-1=0. Таких коалиций только одна: (1,2,3), так как 10+20+30=60>50Þ υ(S)=1 и для (2,3), т.е. без первого игрока, имеем 20+30=50 Þ υ(S\1)=0, т.е. не выигрывающая коалиция Þ υ(S)-υ(S\1)=1-0=1. Остальные выигрывающие коалиции с игроком 1 являются выигрывающими и без него, т.е. игрок 1 не приносит пользы этим коалициям, поэтому здесь его вклад = 0.

2. Для нахождения Ф2 для игрока 2 найдём коалиции, выигрывающие с ним и не выигрывающие без него. Таких коалиций три: (2,4), (1,2,3), (1,2,4).

3. Для нахождения Ф3 для игрока 3 найдём коалиции, выигрывающие с ним и не выигрывающие без него. Таких коалиций три: (3,4), (1,2,3), (1,3,4).
Ф3 вычисляется по тем же данным, что и Ф2 Þ Ф3= 
4. Для нахождения Ф4 для игрока 4 найдём коалиции, выигрывающие с ним и не выигрывающие без него. Таких коалиций пять: (2,4), (3,4), (1,2,4), (1,3,4), (2,3,4).

Имеем вектор Шепли Ф(υ)= 
Для контроля вычислений проверим: Ф1+ Ф2+ Ф3+ Ф4= 
Если посчитать вектор распределения выигрыша традиционно, т.е. пропорционально количества акций, то получим вектор:  .
.
Вектор Шепли учитывает следующие факты: возможности организовывать коалиции из игроков 2 и 3 одинаковы, несмотря на разницу в количестве акций, а для игроков 1 и 4 и возможности по организации коалиций различны, и имеется значительная разница в количестве акций.
Пример 7. Найти вектор Шепли для игры с характеристической функцией:
υ(1)= υ(3)=0; υ(2)=1; υ(1,2)=4; υ(1,3)=3; υ(2,3)=5; υ(1,2,3)=6.
Решение: это не простая игра, поэтому вектор Шепли будем вычислять по формуле (*):
Определим вероятности Р3(1), Р3(2), Р3(3) появления соответственно одноэлементных, двухэлементных, трёхэлементных коалиций с игроком i:
Из общей формулы нахождения вероятности появления k-элементных коалиций с игроком i, где n – общее число игроков Рn(k) =  ,
,
Получаем Р3(1)= 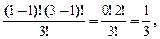 Р3(2)=
Р3(2)= 
Р3(3)= 
1. Для нахождения Ф1 выигрыша для игрока 1 найдём вклад игрока 1 в соответствующие коалиции: а). вклады в одноэлементную коалицию:
υ(1) - υ(Ø)=0-0=0;
б). вклады в двухэлементные коалиции:
υ(1,2) - υ(2)=4-1=3; υ(1,3) - υ(3)=3-0=3;
в). вклады в трёхэлементную коалицию:
υ(1,2,3) - υ(2,3)=6-5=1.
Подставим вычисленные значения формулу (*):
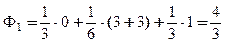
2. Аналогичным образом для нахождения Ф2 для игрока 2 найдём вклад игрока 2 в соответствующие коалиции: а). вклады в одноэлементную коалицию:
υ(2) - υ(Ø)=1-0=1;
б). вклады в двухэлементные коалиции:
υ(1,2) - υ(1)=4-0=4; υ(2,3) - υ(3)=5-0=5;
в). вклады в трёхэлементную коалицию:
υ(1,2,3) - υ(1,3)=6-3=3.
Подставим вычисленные значения формулу (*):

3. Аналогичным образом для нахождения Ф3 для игрока 3 найдём вклад игрока 3 в соответствующие коалиции: а). вклады в одноэлементную коалицию:
υ(3) - υ(Ø)=0-0=0;
б). вклады в двухэлементные коалиции:
υ(1,3) - υ(1)=3-0=3; υ(2,3) - υ(2)=5-1=4;
в). вклады в трёхэлементную коалицию:
υ(1,2,3) - υ(1,2)=6-4=2.
Подставим вычисленные значения формулу (*):

Имеем вектор Шепли Ф(υ)= 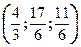
Для контроля вычислений проверим: Ф1+ Ф2+ Ф3= 