1. Статика – это раздел механики, который изучает условия равновесия тел.
2. Равновесие – это состояние покоя в выбранной системе отсчета в течении некоторого промежутка времени. Это означает, что в этом промежутке времени линейная и угловая скорости равны нулю V=0 и ω=0. А для этого необходимо, чтобы в этой системе отсчета линейное ускорение, а=0 и угловое ускорение ε=0.
3. Условие равновесия материальной точки. Простейшее тело – материальная точка – находится в покое, если ее начальная скорость V0 =0 и ускорение, а=0. Откуда следует условие равновесия: равнодействующая всех сил, приложенных к материальной точке R = Σ F i =0 (2-й закон Ньютона).
4. Устойчивое, неустойчивое и безразличное равновесие. Тело, даже находящееся в положении равновесия, может слегка смещаться относительно этого положения в результате каких-либо случайностей и флуктуаций. Например, может слегка изменяться силы, действующие на тело.
Если в результате смещения, появляется равнодействующая сила, направленная к положению равновесия, стремящаяся это равновесие восстановить, то такое равновесие будет устойчивым. Это условие является одновременно и определением, и причиной устойчивого равновесия.
Если при смещении появляется равнодействующая сила, направленная от положения равновесия, то равновесие будет неустойчивым.
Если при смещении тела равнодействующая остается равной нулю, то такое равновесие называется безразличным.
5. Равновесие тела, имеющего размеры. Тело, имеющее размеры может двигаться не только в трех пространственных измерениях, как материальная точка. Оно может вращаться, а также деформироваться, когда одни части тела могут двигаться относительно других. Поэтому условия равновесия для такого тела становится сложнее. Для упрощения этой задачи строится ряд моделей.
6. Абсолютно твердое тело. Это модель тела, которое не может деформироваться, поэтому расстояния между любыми частями такого тела не меняются во времени.
7. Число степеней свободы тела. Число степеней свободы – это число независимых координат, которые нужно зафиксировать, чтобы тело стало неподвижным. Соответственно, это же число возможных независимых друг от друга движений тела. Для материальной точки (МТ) число степеней свободы i равно числу измерений пространства, т.е. I =3. Если тело представляет собой две МТ, скрепленные абсолютно твердым стержнем, то три координаты фиксируют в пространстве одну МТ, в то время, как вторая может совершать вокруг нее два типа вращений. Таким образом, число степеней свободы i=5. Если тело состоит из трех МТ, не лежащих на одной прямой (треугольник), то зафиксировав одну его строну с помощью 5-и переменных, можно видеть, что третья МТ сможет вращаться только в одной плоскости, т.е. у нее останется одна степень свободы. Итого, для жесткого треугольника i=6. Если в любом абсолютно твердом теле зафиксировать 3 точки, не лежащие на одной прямой, то оно будет неподвижно. Значит число степеней свободы абсолютно твердого тела i=6.
8. Движение абсолютно твердого тела. Тело, имеющее 6 степеней свободы, может двигаться свободно так, что все 6 координат одновременно будут изменяться. Есть несколько моделей движения, более простых, чем свободное движение.
Поступательное движение. При поступательном движении все точки тела двигаются по одинаковым траекториям. Поэтому описание поступательного движения тела и движения одной материальной точки совпадают. Если тело может двигаться только поступательно, то условие его равновесия совпадает с условием равновесия материальной точки: сумма сил Σ F i =0
Вращательное движение вокруг неподвижной оси вращения. Ось вращения тела – это линия, все точки которой неподвижны при вращении тела. На самом деле ось вращения может двигаться поступательно – все зависит от выбора системы отсчета. Например, ось вращения колеса автомобиля относительно автомобиля неподвижна, а относительно дороги движется (но не вращается). Может быть и более сложное движение – когда ось вращения сама вращается в пространстве (прецессирует), но мы такое движение рассматривать не будем. Мы будем рассматривать движение, которое состоит максимум из двух независимых движений – поступательного и вращательного вокруг неподвижной оси.
9. Движение абсолютно твердого тела, имеющего закрепленную и неподвижную ось вращения. Если мы выбираем модель тела, имеющего закрепленную ось вращения, то у такого тела число степеней свободы i=1, т.е. оно может только вращаться вокруг этой оси и его положение может зафиксировать одна координата, в качестве которой удобно выбрать угол поворота ϕ, относительно некоторой оси координат. Эксперимент показывает, что если к такому телу приложить силу F, направление которой не проходит через ось вращения, то оно начинает вращаться с ускорением. Хотя при этом сумма исходной силы и силы реакции закрепленной оси – равна нулю, но тело выходит из равновесия. Движение такого тела удобно описывать угловой скоростью вращения ω = Δϕ/Δt, а ускорение – угловым ускорением ε= Δω/Δt.
10. 
Условие равновесия тела, имеющего неподвижную ось вращения. Оказывается, что угловое ускорение тем больше, чем больше сила и чем больше расстояние от оси вращения до линии действия этой силы.
Плечо силы – кратчайшее расстояние (длина перпендикуляра) от оси вращения до линии действия силы.
Момент силы - величина, определяющая угловое ускорение вращения тела: M=F d
Знак момента силы. Если сила стремиться повернуть тело против часовой стрелки, то момент положительный, если по часовой стрелке – отрицательный.
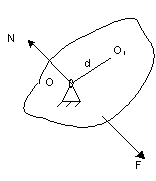Если сумма моментов сил относительно закрепленной оси равна нулю, то угловое ускорение также равно нулю. Можно показать, что если сумма моментов относительно закрепленной оси равна нулю, то и сумма моментов относительно любой точки тела также равна нулю. Пусть к телу приложена сила F так, что ее момент относительно оси вращения Мо =0. Это значит, что линия ее действия проходит через точку О и плечо этой силы d=0. Т.к. тело при этом неподвижно, то сила реакции опоры N =- F. Вычислим момент всех сил, приложенных к телу относительно произвольной точки О1: М(О1) = Fd – Nd = 0, т.к. N=F. Значит условие равновесия тела, имеющего закрепленную ось вращения: «Момент всех сил, приложенных к телу, относительно любой точки равен нулю».
11. Центр тяжести и центр масс тела. Рассмотрим абсолютно твердое тело массой М, находящееся в поле силы тяжести g. Приложим к нему силу реакции опоры (подвеса) N, так, чтобы компенсировать силу тяжести F т = m g. Очевидно, что N =- F т. При этом по 2-му закону Ньютона, а =0. Но в зависимости от точки приложения этой силы тело может не находиться в равновесии, а вращаться. Точка, к которой нужно приложить силу реакции опоры так, чтобы при любом положении тела, оно не вращалось, а находилось в положении равновесия, называется центр тяжести тела.
|
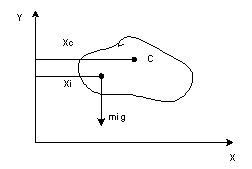
Выведем формулу для нахождения центра тяжести тела. Пусть масса тела М. Разобьем тело на отдельные тела, массой mi, каждое из которых имеет координаты (xi, yi), тогда М=Σmi. И пусть для простоты тело будет плоским. Пусть координаты искомого центра тяжести будут Xc Yc, а вектор g направлен вниз перпендикулярно оси Х. Тогда на каждое тело будет действовать сила тяжести mig, плечо которой будет di=Xc- xi. Условие равновесия относительно точки С будет: Σ mig (Xc- xi) =0. Отсюда ХсΣmi = Σmixi и 
. Повернем теперь тело вместе с системой координат на 90⁰ против часовой стрелки. Теперь вектор g направлен перпендикулярно оси Y и значит координата Yс центра тяжести будет определяться формулой, аналогичной Хс →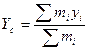 
Центр тяжести тела одновременно является и его центром масс или центом инерции.
Если приложить силу F к материальной точке, то она будет двигаться с ускорением a = F /m. Но если приложить эту силу к абсолютно твердому телу, то в общем случае, оно начнет одновременно вращаться и двигаться поступательно. При этом все его точки будут двигаться с разными ускорениями. Но есть одна точка – точка С, такая что, если приложить силу к ней, то тело не будет вращаться, а будет двигаться поступательно с ускорением a = F /m. Эта точка называется центр масс тела. Координаты точки С определяются по такой же формуле, что и координаты центра тяжести. Центр масс есть не только у абсолютно твердого тела, но и у системы тел.
Смысл центра масс системы тел в том, что если тело мы хотим заменить систему тел или одно большое тело на материальную точку, то она должна иметь массу равную массе тел системы и располагаться в точке центра масс. В частности, можно показать, что суммарный импульс тела, как целого равен массе этого тела умноженный на скорость его центра масс. Если использовать центр масс в качестве системы отсчета, то относительно него суммарный импульс тела системы равен нулю. Например, если ракета, находящаяся в космосе, неподвижна относительно выбранной системы отсчета, то после включения двигателя ее импульс, включая в него и импульс выброшенных газов, так и останется равным нулю и центр масс так и останется неподвижным, хотя ракета улетит неизвестно куда.
Используя понятие центра масс можно любой движение плоского тела представить, как сумму двух движений: поступательного, как движение материальной точки, расположенной в центре масс и вращательного вокруг центра масс.
12. Равновесие жидкости или гидростатика.
12.1. Давление в жидкости, находящейся под действием силы тяжести.
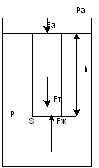Рассмотрим неподвижную жидкость плотностью ρж, находящуюся в открытом сосуде. Сверху на нее давит воздух, находящейся под атмосферным давлением pа. На уровне моря давление примерно равно 105 Па. Вычислим давление p в жидкости на глубине h. Вырежем в жидкости воображаемый цилиндр площадью S и высотой h. Он неподвижен. Значит равнодействующая внешних сил равна нулю. Силы давления на стенки цилиндра уравновешены, поэтому нас будут интересовать только силы, направленные вертикально. На цилиндр действует сила тяжести Fт =mg = ρжShg, сила давления атмосферы Fа = paS и сила давления жидкости Fж = pжS. Условие равновесия Fт + Fа= Fж или ρжShg + paS = pS. Отсюда мы получаем, что давление на глубине h равно р = ра + ρжgh. Это значит, что поле сил давления в данном случае зависит только от одной координаты – h.
Интересно, что произойдет с давлением в жидкости, если данный сосуд станет двигаться с ускорением, а, направленным вверх или вниз. В этом случае, система станет неинерциальной и в ней появится силы инерции. На выбранный нами цилиндр будет дополнительно действовать сила равная ρжSha, направленная в зависимости от направления ускорения a. Если ускорение направлено вниз, то сила инерции направлена вверх и давление р = ра + ρж(g-a)h. В частности, в невесомости, когда a=g, p=pа, т.е. не зависит от глубины h.
13. Сила Архимеда.
Вес тела, погруженного в жидкость уменьшается. Это можно проверить, подвесив тело к пружинным весам и сравнить его вес до погружения в жидкость и после. Это происходит потому, что на погруженное в жидкость тело действует выталкивающая сила (сила Архимеда), направленная против силы тяжести. Найдем формулу для вычисления выталкивающей силы. Для этого представим, что тело погружено в жидкость целиком. Мысленно выделим в теле вертикальный цилиндрик с маленькой площадью основания Δs. Пусть высота цилиндрика h, его верхнее основание находится на глубине h1, а нижнее – h2 = h1 + h. Тогда давление жидкости у верхнего основания p1 = pа + ρжgh1, а у нижнего – p2 = pа + ρжg(h1 + h), где ра – атмосферное давление а ρж – плотность жидкости. Сила давления на верхнее основание Fд1 = р1 Δs, а на нижнее Fд2 = р2 Δs. Результирующая сила направлена вверх и равна Fд2 - Fд1= ρжgh Δs. h Δs = Δw – объем цилиндрика, а Δwρжg – вес жидкости, которую вытеснил цилиндрик. Если просуммировать все силы, действующие на все цилиндрики, то получим, что на тело в жидкости действует сила Fа =ρжgw, где w – суммарный объем всех цилиндриков, т.е. объем всего тела.
Это выражение для выталкивающей силы носит название закон Архимеда: на тело, погруженное в жидкость или газ действует выталкивающая сила, равная весу жидкости, вытесненной телом.
Если вспомнить выражение, полученное для величины давления в системе отсчета, движущейся с вертикальным ускорением, то можно понять, что в такой системе, и архимедова сила зависит от ускорения системы. Fа = wρж (g – а). Из этого выражения видно, что архимедова сила действительно равна весу вытесненной телом жидкости, а не силе тяжести, действующей на жидкость. В невесомости, если g = a, то Fа =0.
Есть еще одно доказательство формулы для силы Архимеда. Если мысленно «убрать» тело и заполнить образовавшееся место жидкостью, то она будет неподвижна. Значит суммарная сила давления жидкости, действующая на этот объем жидкости равна ее весу. А суммарная сила давления жидкости на тело – это и есть сила Архимеда.
13.1. Плавучесть тела в жидкости. Если тело погрузить в жидкость целиком, то его поведение будет зависеть от соотношения силы тяжести и силы Архимеда. Сила тяжесть может быть выражена равенством Fт = ρтgw, где ρт – средняя плотность тела, а w – его объем. Сила Архимеда Fа =ρжgw. Если сила тяжести больше силы Архимеда, т.е. Fт > Fа, то тело тонет. Это происходит, когда ρт > ρж. Если ρт < ρж, то тело всплывает. Остановится оно, когда часть тела окажется над жидкостью и выталкивающая сила, действующая на погруженную в жидкость часть тела станет равной весу всего тела. Пусть объем погруженной части wп, тогда ρтgw = ρжgwп и wп = w ρт/ρж. Если же ρт = ρж, то говорят, что тело имеет нейтральную плавучесть. В этом случае оно будет находится в равновесии в любой точке жидкости.
13.1.1. «Присасывание» тела ко дну. Следует понимать, что сила Архимеда – это результирующая сил давления жидкости, действующих на тело. Поэтому, если нижняя часть тела плотно прижата к дну сосуда, так, что жидкость из-под тела вытеснена, то силы давления на эту, изолированную от жидкости часть тела не будет, и формула для определения силы Архимеда будет не верна. Например, если взять цилиндрик, с отшлифованным дном имеющий положительную плавучесть, опустить его в жидкость и прижать ко дну сосуда, то он не всплывет. Это будет выглядеть, как будто цилиндрик «присосало» ко дну. Такая же участь может постигнуть и подводную лодку, легшую на вязкий грунт. Попытка всплыть путем опорожнения цистерн с водой может закончится неудачей, если вода не поступает под дно лодки и не создает силу давления, которая может ее поднять. В этом случае лодке придется рассчитывать только на силу тяги винтов, которые могут сдвинуть ее так, чтобы вода попала под днище и эффект «присасывания» исчез.
14. Формулы и константы
14.1. Условия равновесия абсолютно твердого тела
14.1.1. ∑ F i = 0
14.1.2. ∑ Mi = 0
14.1.3. Координаты центра тяжести плоского тела: ;
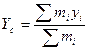
14.2. Давление жидкости на глубине h, если давление атмосферы pa: р = ра + ρжgh
14.3. Сила Архимеда в инерциальной системе отсчета Fа =ρжgw
14.4. Объем погруженной части плавающего тела: wп = w ρт/ρ