План
1) Определения криволинейного интеграла.
2) Криволинейный интеграл 1 рода.
- Свойства
- Вычисление
3) Криволинейный интеграл 2 рода.
- Свойства
- Вычисление
4) Взаимосвязь криволинейных интегралов.
5) Физические приложения
· Масса кривой
· Центр масс и моменты инерции кривой
6) Геометрические приложения
· Длина кривой
· Площадь области, ограниченной замкнутой кривой
· Объем тела, образованного вращением замкнутой кривой относительно оси Ох
Определение криволинейного интеграла.
Криволинейный интеграл — интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве. Существуют интегралы первого и второго рода.
Пусть L – гладкая, без особых точек и самопересечений кривая(допускается одно самопересечение – случай замкнутой кривой), заданная параметрически.
-(отрезок параметризации)-рассматриваем часть кривой.
Пусть 
– разбиение отрезка параметризации [a,b], причем 
Зададим разбиение кривой 
За 
, k = 1,n.
Введем мелкость разбиения отрезка параметризации
Введем набор промежуточных точек разбиения отрезка параметризации
Зададим набор промежуточных точек разбиения кривой
Пусть нам также даны 4 функции, которые определены вдоль кривой
L: f(x,y,z), P(x,y,z), Q(x,y,z), R(x,y,z).
Рассмотрим 4 интегральные суммы.
1. Интегральная сумма криволинейного интеграла второго рода: 
2. Три интегральные суммы криволинейного интеграла второго рода: 
Если 
интегрируема в смысле криволинейного интеграла первого рода по кривой L, а сам предел называют криволинейным интегралом первого рода функции f по кривой L и обозначают
, где dl – дифференциал кривой.
Если 
, то говорят, что функции P,Q,R интегрируемы в смысле криволинейного интеграла второго рода по кривой L, а сами пределы называют криволинейными интегралами второго рода функций P, Q, R по кривой L и обозначают
|
|
Криволинейный интеграл первого рода.
Свойства:
1. Линейность 
2. Аддитивность: если L1 пересекает L2 в одной точке, то 
3. Монотонность: если f 
4. Теорема о среднем для непрерывной вдоль L функции f: 
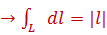
5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: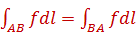 
6. Криволенейный интеграл первого рода не зависит от параметризации кривой
Вычисление:
Пусть L – гладкая, спрямляемая кривая, заданная параметрический (как в определении). Пусть функция f(x,y,z) определена и интегрируема вдоль кривой L в смысле криволинейного интеграла первого рода. Тогда
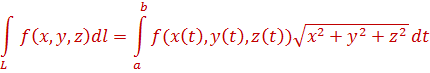
Пример:
Найти интеграл 
вдоль отрезка y = x от начала координат до точки (2,2)
Криволинейный интеграл второго рода.
Свойства:
1. Линейность 
2. Аддитивность 
3. Монотонность: если f ≤ g на P, то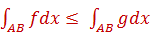 
4. Оценка модуля 
5. Теорема о среднем: если f непрерывна на Р, то 
, такая что: 
6. 
Вычисление:
Пусть L гладкая, спрямляемая кривая, заданная параметрический(как в определении). Пусть функция f(x,y,z) определена и интегрируема вдоль кривой L в смысле криволинейного интеграла второго рода. Тогда
, 
, 
Если обозначить за 
единичный вектор касательной к кривой L, то нетрудно показать, что
x’(t)dt = cos( 
^ 
)dl
y’(t)dt = cos( 
^ )dl
z’(t)dt = cos( 
^ )dl
Пример:
Вычислить интеграл 
, где кривая L задана параметрически в виде 
(t) = (cost, sint), 
,
