Кафедра Электропривода и автоматизации производственных процессов
ДОКЛАД
По дисциплине: Физика
на тему:«Следствия из теоремы Гаусса»
Выполнил: студент гр. ЭО-19
Хартаев Валерий Андреевич
Проверил: Доцент и зав. каф. ЭПиАПП
Мусакаев М.А.
Нерюнгри 2020
Содержание
| Введение | |
| Теорема Гаусса | |
| Применение теоремы Гаусса | |
| Следствия из теоремы Гаусса | |
| Список используемой литературы |
Введение
В 1831 году Карл Фридрих Гаусс вместе со своим молодым коллегой Вильгельмом Вебером занялся изучением электричества и магнетизма. Вскоре он сформулировал, и доказал теорему, названную его именем. Чтобы понять, в чем заключается ее смысл, представьте себе изолированный точечный электрический заряд q, окруженный замкнутой поверхностью. Форма поверхности в теореме не имеет значения. В каждой точке, окружающей заряд поверхности наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. Теорема Гаусса как раз и гласит, что суммарный поток напряженности электрического поля, проходящий через окружающую заряд поверхность, пропорционален величине заряда.
Теорема Гаусса
Теорема Гаусса является важнейшей теоремой электростатики и формулируется следующим образом:
Теорема Гаусса: поток Ф вектора напряженности электрического поля Е через произвольную замкнутую поверхность S равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на 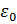 .
.
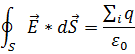
Применение теоремы Гаусса
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R. Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.).
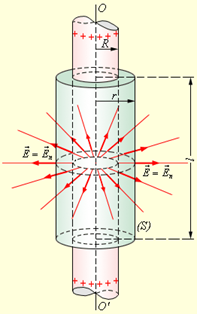
Рисунок 1 “Иллюстрация поля однородно заряженного цилиндра. OO' – ось симметрии.”
Если r≥R, то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим:
Φ=E2πrl= 
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
E= 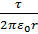
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r<R. В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ=E2πrl. Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис.2).
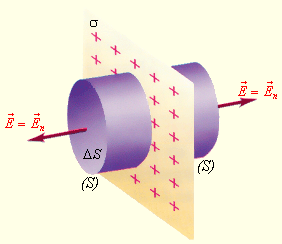
Рисунок 2. “Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.”
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2EΔS= 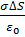 или E=
или E= 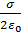
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.