Проверка гипотезы нормальности по совокупности выборок

КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА-КАИ

 

Учебное пособие по выполнению лабораторных работ по испытаниям

 

Казань 2016

 

 

Составители: доцент И.А. Горбунов, проф. Ф.А. Карамов

 

УДК

Учебное пособие по выполнению лабораторных работ/Казан. нац. исслед. техн. ун-т; Сост. доцент И.А. Горбунов, проф. Карамов Ф.А., Казань, 2015 г./.

Пособие предназначено для проведения лабораторных работ с использованием ИК-Фурье спектрофотометра для получения спектральных характеристик (спектрограмм) материалов электроники в ближней, средней и дальней ИК-областях.

 

Табл. __. Ил. __. Библиограф.: __ назв.

ОЦЕНКА ВИДА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Критерий Шапиро-Уилка

Предложено много критериев и способов оценки вида распределения непрерывной случайной величины. Критерий Шапиро-Уилка используется для проверки гипотезы о нормальном распределении. Этот критерий надёжен при 8<=n<=50 (существует модифицированный критерий Шапиро-Уилка, применимый при n до 2000), и является более мощным, чем другие, критерии, т.е. даёт наименьшую вероятность принять нулевую гипотезу, когда на самом деле верна альтернативная, в данном случае – принять гипотезу о нормальном распре-делении, когда распределение не соответствует нормальному.

При использовании критерия результаты испытаний располагают в вариационный ряд и рассчитывают значения

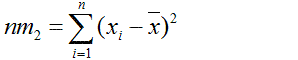
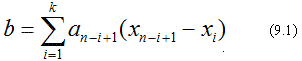
i – номер элемента в вариационном ряду. При этом, если n чётное, k=n/2, если n нечётное, k=(n-1)/2. Значения a_n-i+1 находят из таблиц. Однако с приемлемой точностью значения а можно найти по зависимостям из табл. 9.1.

Таблица 9.1.

i	an-i+1
	(0,0081356n4 - 1,3596n3 + 87,592n2 - 2808,2n + 78028)/100000
	(0,0005642n5 - 0,096475n4 + 6,418n3 - 204,59n2 + 2849,1n + 19225)/100000
	(-0,000053n6 +0,010464n5 - 0,83717n4 + 35,172n3 - 823,97n2 + 10190n - 26059)/100000
	(-0,00008785n6 + 0,017143n5 - 1,3644n4 + 56,8921n3 - 1321,67n2 + 16417,8n - 64907)/100000
	(-0,0000637n6 + 0,012953n5 - 1,08323n4 + 47,9523n3 - 1197,88n2 + 16280,8n - 77227)/100000
	(0,001213n5 - 0,22039n4 + 15,932n3 - 578,01n2 + 10675,3n - 64930)/100000
	(0,001058n5 - 0,19846n4 + 14,8811n3 - 563,328n2 + 10954n - 74246)/100000
	(0,0009663n5 - 0,18425n4 + 14,2448n3 - 558,464n2 + 11321,7n - 83480)/100000
	(0,000936n5 - 0,18321n4 + 14,431n3 - 578,383n2 + 12047,5n - 94506)/100000
	(-0,021445n4 + 3,5688n3 - 227,115n2 + 6687n - 66534)/100000
	(-0,01937n4 + 3,3178n3 - 218,207n2 + 6675n - 70767)/100000
	(-0,01757n4 + 3,0973n3 - 210,36n2 + 6671,5n - 74844)/100000
	(-0,01577n4 + 2,8668n3 - 201,302n2 + 6621,8n - 78311)/100000
	(0,4448n3 - 64,902n2 + 3325n - 51098)/100000
	(0,4227n3 - 63,247n2 + 3332,2n - 53673)/100000
	(0,4046n3 - 61,999n2 + 3353,2n - 56378)/100000
	(0,3853n3 - 60,444n2 + 3354,8n - 58703)/100000
	(0,3532n3 - 57,207n2 + 3282,5n - 59931)/100000
	(-11,224n2 + 1322,1n - 33480)/100000
	(-11,072n2 + 1331,1n - 35023)/100000
	(-10,898n2 + 1337,8n - 36508)/100000
	(-10,833n2 + 1354,4n - 38200)/100000
	(-10,714n2 + 1365,6n - 39754)/100000
	(335n - 15708)/100000
	0,0035

Статистику критерия рассчитывают по формуле W =b²/nm₂. Рассчитанное значение W сравнивают с табличным W_табл. Табличные значения критерия W_табл в зависимости от уровня значимости α находят из таблиц, однако с приемлемой точностью их можно найти по зависимостям, показанным в табл. 9.2.

Таблица 9.2.

α	Wтабл
0,01	(-0,0148n4 + 2,1875n3 - 122,61n2 + 3257,3n + 55585)/100000
0,05	(-0,0113n4 + 1,656n3 - 91,88n2 + 2408,6n + 67608)/100000
0,1	(-0,0084n4 + 1,2513n3 - 70,724n2 + 1890n + 73840)/100000

Если W >= Wтабл, нулевую гипотезу не бракуют, т.е. распределение считают нормальным.

Пример 9.1. По данным примера 1.1 проверить при различных уровнях значимости гипотезу о нормальности распределения предела прочности на разрыв алюминиевого сплава.

Вариант выполнения примера 9.1 показан на рисунке 9.1.

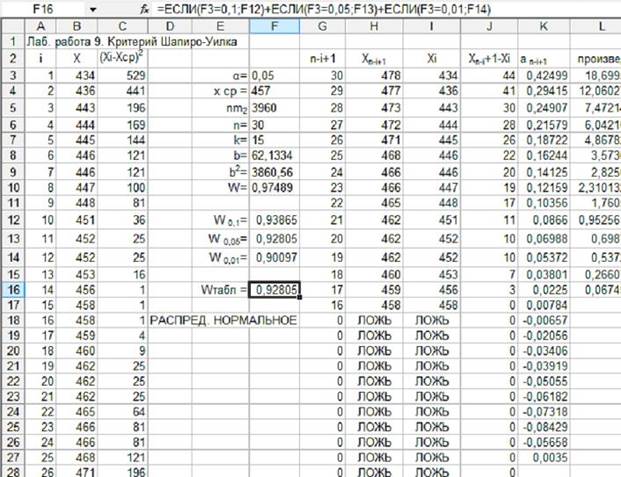
Рис. 9.1. Вариант расчёта для примера 9.1.

Вводим в электронную таблицу уровень значимости и результаты испытаний, упорядочиваем их в вариационном ряду, рассчитываем среднее значение, сумму квадратов отклонений от среднего nm₂, объём испытаний (какие при этом целесообразно задать в статистических функциях диапазоны?), а также величину k. Очевидно, что для любого (чётного и нечётного) n можно рассчитать k по формуле k=n/2 с округлением результата вниз до целого (функция ОКРУГЛВНИЗ).

Далее находим b. Для этого вначале рассчитываем значения n-i+1. Поскольку при этом, в соответствии с формулой (9.1), i <= k, при расчёте используем функцию ЕСЛИ, в которой логическим выражением будет i <= k. При его истинности принимается значение n-i+1, при ложности - 0. (Не забывайте установить в необходимых случаях абсолютную адресацию). Затем находим значения x_n-i+1. Поскольку n-i+1>= k, при расчёте используем функцию ЕСЛИ, в которой логическим выражением будет n-i+1>= k (т.е. ссылка на ячейку столбца G). При истинности этого выражения значение x_n-i+1 находим при помощи функции ИНДЕКС, при ложности значение не задаём. Затем находим x<subi< sub=""></subi<> используя функцию ЕСЛИ, и далее - разности x_n-i+1 - x_i. Рассчитываем значения a_n-i+1 по формулам табл. 7.1. Находим произведения a_n-i+1(х_n-i+1-x_i), и по их сумме – величину b, а затем b² и W. Рассчитываем табличные значения критерия для различных уровней значимости по формулам табл. 7.2. Из этих значений выбираем необходимое Wтабл в соответствии с заданным уровнем значимости, используя трижды функции ЕСЛИ.

Затем, если n < 8, с помощью функции ЕСЛИ выводим сообщение «ВЫБОРКА СЛИШКОМ МАЛА». При ложности этого логического выражения используем в строке Значение_если_ложь функцию ЕСЛИ для сравнивания W и Wтабл, и в зависимости от истинности или ложности логического выражения выводим сообщение, является ли распределение нормальным. В результате в одной ячейке (в при-мере – ячейка D18) должно выводиться одно из трёх сообщений, на-пример: ВЫБОРКА СЛИШКОМ МАЛА; РАСПРЕД. НОРМАЛЬНОЕ; РАСПРЕД. НЕ НОРМАЛЬНОЕ.

При правильном выполнении электронная таблица должна вер-но пересчитываться при вводе других данных в пределах применимо-сти критерия Шапиро-Уилка.

Задание.
1. Выполнить расчёты в соответствии с примером 9.1.
2. Выборочные значения случайных величин, полученные по ре-зультатам испытаний, показаны в табл. 9.3.

Таблица 9.3.

№ выборки	Р	Значения в выборке
	0,9	855 875 834 872 863 855 888 864 870 881 891 872
	0,95	11 12 9 16 12 8 9 10 10 9 11 10 8 8
	0,99	34 36 38 33 34 32 30 36 38 31

Виды распределений случайных величин неизвестны. Используя созданные электронные таблицы, исключить грубые ошибки (по ка-кому критерию?), определить, какие из случайных величин могут быть описаны нормальным распределением, в случае нормального распределения рассчитать интервальные оценки параметров этих распределений. Результаты занести в таблицу 9.4.

Таблица 9.4.

№ выборки	Грубые ошибки	Распределение (норм/не норм)	Оценка М	Оценка σ
точечная	Интерв.	точечная	Интерв.
	...	...	...	....	...	...
	...	...	...	....	...	...
	...	...	...	....	...	...

 

Критерий омега-квадрат

Критерий омега-квадрат (ω², другое название – критерий Крамера-Мизеса-Смирнова) достаточно надёжен при n >= 15 для проверки гипотезы, подчиняется ли случайная величина некоторому закону распределения, если известны его параметры (простая гипотеза). Проверка может проводиться для любого вида распределения. Критерий основан на определении суммы квадратов разностей между накопленной частостью (эмпирической функцией распределения) и теоретической функцией распределения.

Результаты испытаний располагают в вариационном ряду. Статистику критерия можно рассчитать по формуле

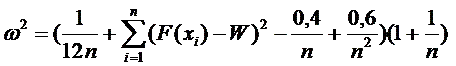(10.1)

Здесь F(x_i) – значения теоретической функции предполагаемого распределения; W=(2i-1)/2n – накопленная частость.

Расчётное значение сравнивают с табличным ω²_табл, значения которого приведены в табл. 10.1.

Таблица 10.1.

α	0,1	0,05	0,01
ω2табл	0,347	0,461	0,743

Если ω² <= ω²_табл, то нулевую гипотезу не бракуют, т.е. распределение считают соответствующим теоретическому с функцией распределения F(x) с известными параметрами при выбранном уровне значимости α.

Если параметры предполагаемого распределения заранее неизвестны, критерий, называемый в этом случае «критерий типа омега-квадрат», может использоваться только для некоторых видов распределений, с использованием вместо параметров их выборочных оценок. При этом определяется, принадлежит ли распределение случайной величины тому или иному семейству распределений, например, нормальных, экспоненциальных и др. (сложная гипотеза). Так, для нормального распределения результаты испытаний располагают в вариационном ряду. Статистику критерия для нормального распределения можно рассчитать по формуле

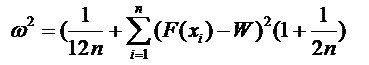(10.2)

Здесь F(x_i) – значения функции нормального распределения (функция НОРМРАСП, в строке Интегральная диалогового окна ввести слово ИСТИНА) с параметрами М и σ, соответствующими их оценкам x_ср и s; W=(2i-1)/2n – накопленная частость.

Расчётное значение сравнивают с табличным ω²_табл. Значения ω²_табл зависят от вида распределения. Для нормального распределения они приведены в табл. 10.2.

Таблица 10.2.

α	0,1	0,05	0,01
ω2табл	0,104	0,126	0,179

Если ω² < ω²_табл, то нулевую гипотезу не бракуют, т.е. распределение считают соответствующим предполагаемому с выбранным уровнем значимости α.

Пример 10.1. При испытаниях образцов алюминиевого сплава получены значения относительного сужения: 0,320 0,327 0,390 0,409 0,285 0,292 0,305 0,308 0,252 0,420 0,340 0,430 0,261 0,310 0,360 0,298 0,299 0,313 0,315 0,290. Проверить гипотезу о нормальном распределении относительного сужения при различных уровнях значимости. Предусмотреть возможность расчёта для объёма испытаний до 1000.

Вариант выполнения примера 10.1 показан на рис. 10.1.

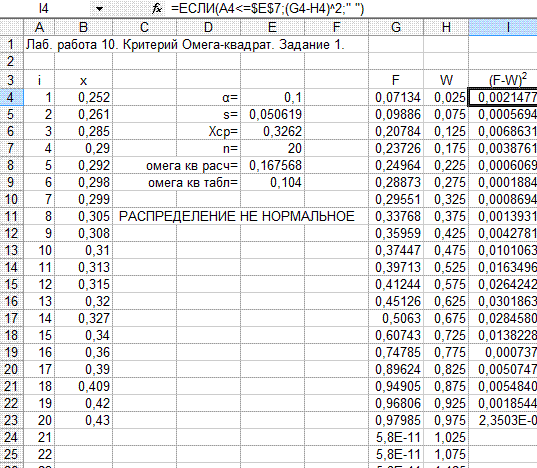
Рис.10.1. Вариант расчёта для примера 10.1.

Поскольку параметры предполагаемого нормального распределения неизвестны, значение критерия рассчитываем по формуле (10.2).

Пример 10.2. При статистической обработке результатов испытаний получена выборка значений непрерывной случайной величины Х: 0,18 0,11 -0,31 -0,69 -0,35 -0,46 -2,16 -0,33 0,58 1,54 1,32 1,67 -0,77 -0,55 -0,40 -1,48 -1,32 0,89. Проверить гипотезу о том, что Х подчиняется распределению Стьюдента, при различных уровнях значимости. Предусмотреть возможность расчёта для объёма испытаний до 1000.

Вариант выполнения примера 10.2 показан на рис. 10.2.

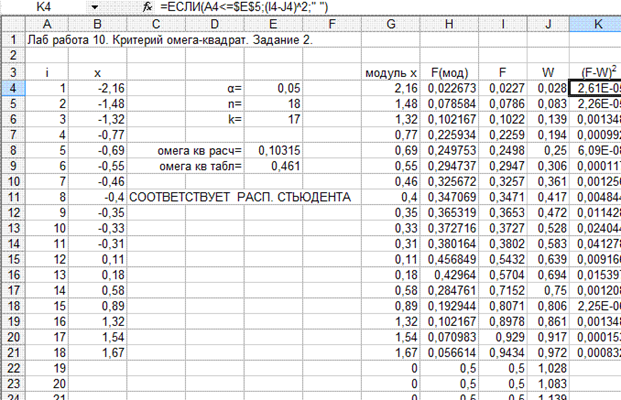
Рис.10.2. Вариант расчёта для примера 10.2.

Распределение Стьюдента имеет единственный параметр – число степеней свободы k. В данном случае k=n-1, т.е. параметр известен. Поэтому значение критерия рассчитываем по формуле (10.1).

Число степеней свободы возможно рассчитать, но лучше вводить его с клавиатуры, т.к. при решении некоторых других задач оно может рассчитываться по другим зависимостям. Значения функции распределения Стьюдента F(x) в Excel находятся по функции СТЬЮДРАСП. Однако при этом функция СТЬЮДРАСП непосредственно рассчитывается только от неотрицательных аргументов, и притом в виде значений, равных 1- F(x). Для отрицательных аргументов функция распределения Стьюдента может быть найдена по функции СТЬЮДРАСП от модуля аргумента. Поэтому для нахождения функции распределения Стьюдента сначала находим модуль каждого значения выборки (столбец модуль х, функция ABS). Затем находим значения функции СТЬЮДРАСП от модулей значений выборки (столбец F(мод), При этом Хвосты в диалоговом окне принимаем 1, т.е. одностороннее распределение. Наконец, находим значения функции распределения Стьюдента (столбец F), используя функцию ЕСЛИ: если элемент выборки (по существу, квантиль распределения Стьюдента) больше нуля, F = 1 - F(мод), иначе F = F(мод).

Пример 10.3. По результатам испытаний получена выборка значений непрерывной случайной величины Х: 2,4 2,6 2,6 2,8 2,9 2,9 2,9 3,6 4,6 4,9 5,0 5,0 5,1 5,1 5,2 5,3 5,4 5,7 5,8 5,8 6,0. Проверить при различных уровнях значимости гипотезу о том, что Х подчиняется равномерному распределению с параметрами a = 2, b = 6. Предусмотреть возможность расчёта для объёма испытаний до 1000.

Вид функции равномерного распределения показан на рис 10.3.

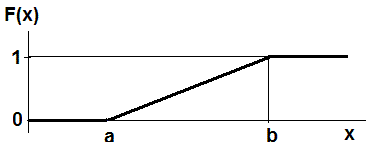
Рис.10.3. Вариант расчёта для примера 10.3.

Равномерное распределение имеет параметры a и b.
При х < a F(x) = 0
При х > b F(x) = 1
При a < х < b F(x) = (x-a)/(b-a)

Поскольку параметры a и b известны, значение критерия ω² рассчитываем по формуле (10.1).

Вариант выполнения примера 10.3 показан на рис. 10.4. Значения в столбце (F-W)² рассчитываем с использованием функции ЕСЛИ аналогично примеру 10.2.

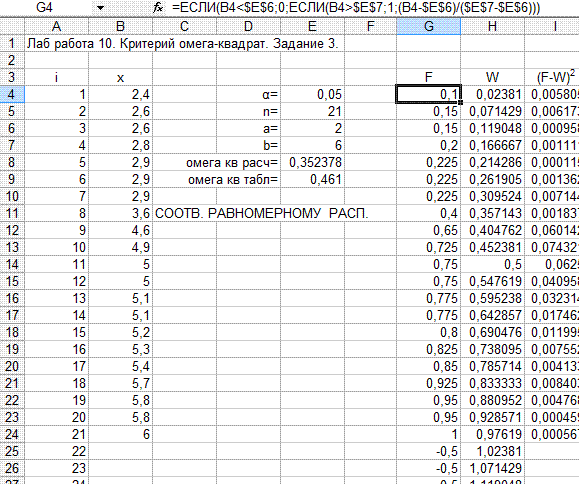
Рис.10.4. Вариант расчёта для примера 10.3.

Задание.
1. Выполнить расчёты в соответствии с примером 10.1.
2. Выполнить расчёты в соответствии с примером 10.2.
3. Выполнить расчёты в соответствии с примером 10.3.
4. Результаты расчётов привести в табл. 10.3.

Таблица 10.3

№	Проверяемое распределение	Известны ли параметры (да/нет)	Соответствие проверяемому распределению (+/-)
α=0,01	α=0,05	α=0,1
ω2	ω2табл	+ -	ω2	ω2табл	+ -	ω2	ω2табл	+ -
	Нормальное
	Стьюдента
	Равномерное

 

Критерий Колмогорова

Критерий Колмогорова (другое название – критерий Колмогорова-Смирнова) достаточно надёжен при n >= 15..20 для проверки гипотезы, подчиняется ли случайная величина некоторому закону распределения, если известны его параметры (простая гипотеза). Проверка может проводиться для любого вида распределения. Критерий основан на определении максимального отклонения накопленной частости (эмпирической функции распределения) от теоретической функции распределения.

Результаты испытаний располагают в вариационном ряду. Находят верхнюю и нижнюю границы соответствующего отклонения:

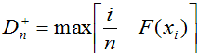при 1 <= i <= n (11.1)

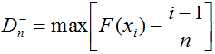при 1 <= i <= n (11.2)

Здесь F(x_i) – значения теоретической функции предполагаемого распределения.

Выбирают максимальную из границ отклонений:

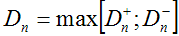(11.3)

Статистику критерия можно рассчитать по формуле

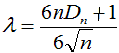(11.4)

Расчётное значение сравнивают с табличным λ_табл, значения которого приведены в табл. 11.1.

Таблица 11.1.

α	0,1	0,05	0,01
λтабл	1,224	1,358	1,628

Если λ_расч <= λ_табл, то распределение считают соответствующим теоретическому с функцией распределения F(x) с известными параметрами при выбранном уровне значимости α.

Если параметры предполагаемого распределения заранее неизвестны, критерий, называемый в этом случае «критерий типа Колмогорова», может использоваться только для некоторых видов распределений, с использованием вместо параметров их выборочных оценок. При этом определяется, принадлежит ли распределение случайной величины тому или иному семейству распределений, например, нормальных, экспоненциальных и др. (сложная гипотеза). Так, для нормального распределения результаты испытаний располагают в вариационном ряду. Находят D_n по формулам (11.1) – (11.3), с учётом того, что F(x_i) – значения функции нормального распределения (функция НОРМРАСП, в строке Интегральная диалогового окна ввести слово ИСТИНА) с параметрами М и σ, соответствующими их оценкам 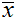и s; Статистику критерия для нормального распределения можно рассчитать по формуле (11.4).

Расчётное значение сравнивают с табличным λ_табл, значения которого приведены в табл. 11.2.

Таблица 11.2.

α	0,1	0,05	0,01
λтабл	0,819	0,895	1,035

Если λ_расч <= λ_табл, то нулевую гипотезу не бракуют, т.е. распределение считают соответствующим предполагаемому.

Пример 11.1. По данным примера 10.1 по критерию Колмого-рова проверить гипотезу о нормальном распределении относительно-го сужения сплава алюминия при различных уровнях значимости. Предусмотреть возможность расчёта для объёма испытаний до 1000. Вариант выполнения примера 11.1 показан на рис. 11.1.

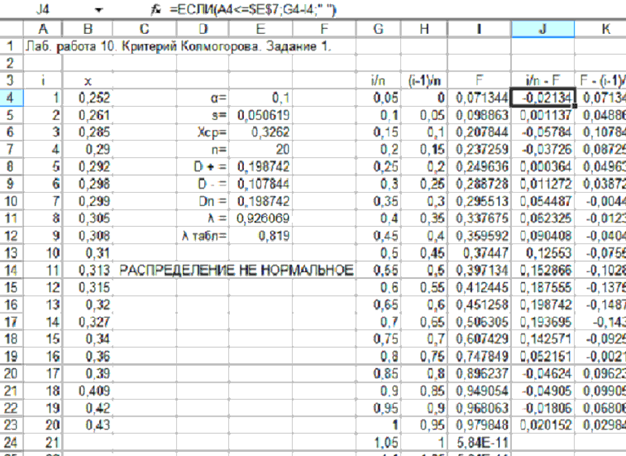
Рис.11.1. Вариант расчёта для примера 11.1.

Задание.
1. Выполнить расчёты в соответствии с примером 11.1.
2. По данным примера 10.2 проверить гипотезу о распределении Стьюдента непрерывной случайной величины Х при различных уровнях значимости.
3. По данным примера 10.2 проверить гипотезу о нормальном стандартном распределении непрерывной случайной величины Х при различных уровнях значимости (Функция нормального стандартного распределения находится по статистической функции НОРМСТРАСП, её параметры, М = 0 и σ = 1, вводить с клавиатуры не надо, т.к. они учтены в НОРМСТРАСП).
4. По данным примера 10.2 проверить гипотезу о равномерном распределении непрерывной случайной величины Х с параметрами a= - 2,2 и b=1,7 при различных уровнях значимости.
5. Привести результаты расчётов в заданиях 1 – 3 в табл. 11.3.

Таблица 11.3.

№ примера	Прверяемое распределение	Параметры распределения	Соответствие предполагаемому распределению
α =0,01	α =0,05	α =0,1
λ	λтабл	+/-	λ	λтабл	+/-	λ	λтабл	+/-
11.1	Нормальное	Неизв.
10.2	Стьюдента	k =
10.2	Нормальное Стандартное	М = σ =
10.2	Равномерное	а = b =

 

Проверка гипотезы нормальности по совокупности выборок

Если объем многократных измерений очень мал (n < 8), надёжно оценить вид функции распределения характеристики по одной выборке нельзя. Но если есть результаты измерений большого числа выборок одного объема n, например, при текущих контрольных испытаниях партий продукции, можно проверить гипотезу нормальности независимых генеральных совокупностей, из которых взяты выборки, даже если параметры функций распределения этих совокупностей неравны.

Из каждой k -й выборки берут случайным образом один результат x_ik), и рассчитывают для каждой выборки величину

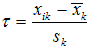
При n = 4 проверяют соответствие распределения τ равномерному распределению с параметрами a = - 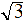и b = 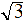(о равномерном распределении см. пример 10.3). Если распределение τ равномерное, то исходные генеральные совокупности подчиняются нормальному распределению. Проверка проводится по любому критерию согласия, например, по критерию омега-квадрат.

При n ≠ 4 вычисляют

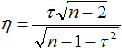
Если η (эта) подчиняется распределению Стьюдента с числом степеней свободы n-2, то исходные генеральные совокупности подчиняются нормальному распределению. Проверка проводится по любому критерию согласия, например, по критерию омега-квадрат.

Учитывая лёгкость автоматического пересчёта, целесообразно провести проверку по критерию согласия многократно, каждый раз выбирая случайным образом новые значения x_ik.

Пример 12.1. В лаборатории систематически проводили испытания партий бумаги различных марок на воздухопроницаемость. Значение воздухопроницаемости, см³/мин, находили как среднее из пяти определений. Результаты приведены в табл. 12.1.

Таблица 12.1.

№ партии	Номер образца	№ партии	Номер образца

Проверить, соответствуют ли распределения величин воздухопроницаемости в выборках нормальным при уровне значимости 0,95.

Фрагмент выполнения примера 12.1 показан на рис. 12.1.

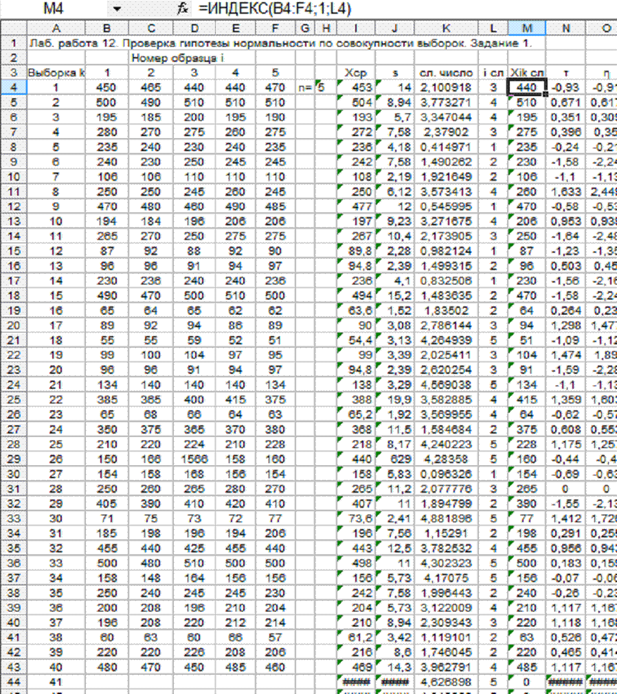
Рис. 12.1. Фрагмент выполнения примера 12.1.

Поскольку n ≠ 4, необходимо рассчитать значения η для каждой выборки и оценить соответствие распределения η распределению Стьюдента.

Вводим исходные данные (предусмотреть количество выборок до 1000), по любой из выборок находим объём единичной выборки n (функция СЧЁТ). Для каждой выборки находим среднее значение и выборочное СКО.

Затем из каждой выборки берём одно случайно выбранное зна-чение x_ik. Для этого по функции СЛЧИС() находим случайное число в диапазоне 0..1, и умножая его на объём одной выборки, получаем случайное число в диапазоне от 0 до объёма выборки (столбец сл. число). (При этом изначально выбранные случайные числа будут меняться при каждом изменении таблицы, однако это не имеет значения, т.к. всё равно они будут случайными, что и нужно). Округляя это число до целого в сторону увеличения (функция ОКРУГЛВВЕРХ), получаем случайно выбранный номер элемента выборки (столбец i сл). С помощью функции ИНДЕКС по этому номеру находим значение случайно выбранного элемента выборки. Далее рассчитываем величины τ и η. Диапазон со значениями η копируем в электронную таблицу, в которой по критерию омега-квадрат оценивается соответствие экспериментального распределения распределению Стьюдента (команда Копировать - Специальная вставка - Значения). Перед копированием необходимо временно снять защиту листа, иначе будет недоступна сортировка η по возрастанию, т.е. в вариационный ряд. Следует также ввести нужные значения числа степеней свободы и уровня значимости.

Пример 12.2. В лаборатории систематически проводили испы-тания партий противокоррозионной бумаги различных марок на со-держание ингибитора. Содержание ингибитора в бумаге, г/м², находили как среднее из четырёх определений. Результаты за некоторый период приведены в табл. 12.2. Проверить, соответствуют ли распределения величин содержания ингибитора в выборках нормальным при уровне значимости 0,95.

Таблица 12.2.

№ партии	Номер образца	№ партии	Номер образца
	8,1	7,9	8,5	8,3		4,5	4,7	4,2	4,3
	7,8	8,2	8,2	8,2		8,3	7,9	8,2	8,1
		8,8	8,6	8,6		8,3	7,8	8,2	8,3
	3,5	3,6	3,8	3,8		8,8	9,1	8,7	8,7
	8,7	8,8	8,5	8,9		3,7	3,5	3,8	3,8
	3,8	3,8	3,9	3,9		8,9	8,8	8,4	8,5
	4,1		3,9	3,9		3.8	3,8		3,9
	9,2	9,1	9,1	9,2		4,1	4,1	3,9	4,1
	8,8	8,7	8,8	8,9		9,4	9,1	9,3	9,2
	3,6	3,6	3,5	3,7		8,8	8,7	8,8	8,9
	3,8	3,8	3,8	3,9		3,6	3,6	3,5	3,7
	2,9	3,2	3,1	2,9		3,9	3,8	3,8	3,9
	3,7	3,6	3,5	3,6		2,9	3,2	3,1	2,9
	3,5	3,6	3,5	3,7		3,7	3,6	3,6	3,4
	3,4	3,5	3,6	3,6		3,5	3,3	3,5	3,7
	8,3	8,2	8,3	8,3		3,4	3,5	3,6	3,6
	8,7	8,9	8,9	8,6		8,4	8,4	8,3	8,4
	9,1	9,2	9,3	9,2		8,7	8,9	8,8	8,6
	9,1	9,1				9,2	9,4	9,3
	3,8	3,8	3,6	3,6		9,1		8,8	9,2
	3,5	3,6	3,7	3,6		3,8	3,8	3,6	3,6
	3,4	3,4	3,4	3,3		3,5	3,6	3,7	3,6
	4,1	4,1	4,3	4,1		3,4	3,4	3,4	3,3
	2,8	2,9				4,1	4,1	4,2	3,9
	3,6	3,6	3,7	3.7		2,8	2,8	3,1

Поскольку n = 4, необходимо оценить соответствие распределения величины τ равномерному распределению.

Диапазон со значениями τ копируем в электронную таблицу, в которой по критерию омега-квадрат оценивается соответствие экспериментального распределения равномерному (команда Копировать - Специальная вставка - Значения). Перед копированием временно снять защиту листа, иначе будет недоступна сортировка τ по возрастанию, т.е. в вариационный ряд. Следует также ввести нужные значения параметров равномерного распределения и уровня значимости.

Задание.
1. Выполнить расчёты по примеру 12.1. Для различных уровней значимости провести проверку нормальности десять раз при изме-няющихся случайных числах. Результаты занести в табл. 12.3.

Таблица 12.3.

№ проверки	Соответствие воздухопроницаемости нормальному распределению (+/-)
α = 0,01	α = 0,05	α = 0,1
ω2	ω2табл	+/-	ω2	ω2табл	+/-	ω2	ω2табл	+/-
% для +

2. Выполнить расчёты по примеру 12.2. Для различных уровней значимости провести проверку нормальности десять раз при изме-няющихся случайных числах. Результаты занести в табл. 12.4.

Таблица 12.4.

№ проверки	Соответствие воздухопроницаемости нормальному распределению (+/-)
α = 0,01	α = 0,05	α = 0,1
ω2	ω2табл	+/-	ω2	ω2табл	+/-	ω2	ω2табл	+/-
% для +