Модель поставок со скидкой

Модель производственных поставок

 

В основной модели предполагалось, что поступление товаров на склад происходит мгновенно. Это предположение достаточно хорошо отражает ситуацию, когда товар поставляется в течении одного дня (или ночи). Если товары поставляются с работающей производительной линии, необходимо модифицировать основную модель. В этом случае к параметрам c, d, s и h добавляется еще один – производительность линии p (единиц товара в год). Будем считать ее заданной и постоянной.

Эта новая модель называется моделью производственных поставок. Величина q по – прежнему обозначает размер партии. В начале каждого цикла происходит «подключение» к производственной линии, которое продолжается до накопления q единиц товара. После этого пополнения запасов не происходит до тех пор, пока не возник дефицит.

График функции изменения запаса имеет вил, изображенный на рис. 3.

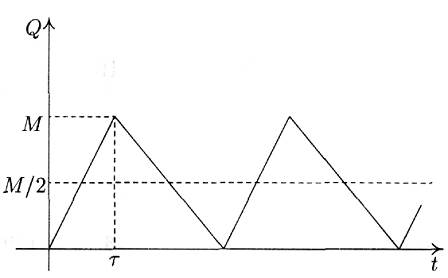
Рис.3

 

Пример 2. Интенсивность равномерного спроса составляет 1 тыс. единиц товара в год. Товар поставляется с конвейера, производительность которого составляет 5 тыс. единиц в год. Организационные издержки равны 10 УЕ, издержки на хранение – 2 УЕ, цена единицы товара – 5УЕ.

Чему равен оптимальный размер партии?

Решение. Имеем:

d = 1000, p = 5000, s = 10, h = 2, c = 5.

Далее,

 

 

 

В итоге получаем

 

Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год n^* и соответствующие продолжительность поставки т^* и продолжительность цикла пополнения запаса t^*:

 

 

дней,

 

 

Общие издержки С(q), как и в основной модели, состоят из трех частей.

А. Общая стоимость товара в год равна

cd.

В. Годовые организационные издержки равны

.

В. Издержки за хранение вычисляются следующим образом. Пусть τ – время поставки (рис. 3). В течении этого времени происходит как пополнение (с интенсивностью p), так и расходование (с интенсивностью d) запаса. Увеличение запаса происходит со скоростью p – d. Поэтому достигнутый к концу периода пополнения запаса максимальный его уровень М вычисляется по формуле

М = (p – d) τ

 

(заметим, что М<q). Однако,

 

pτ = q

(за время τ при интенсивности производства p произведено q единиц товара). Из последних двух равенств следует, что

 

.

 

Средний уровень запаса, как и в основной модели, равен половине максимального, т.е. М/2. Таким образом, издержки за хранение запаса равны

 

день.

 

 

 

 

Общие издержки вычисляются по формуле

 

 

Оптимальный размер поставок q^* получаем из уравнения

 

 

Имеем:

 

 

Модель поставок со скидкой

 

Рассмотрим ситуацию, описываемую в целом основной целью, но с одной особенностью, которая состоит в том, что товар можно поставлять по льготной цене (со скидкой), если размер партии достаточно велик. Иными словами, если размер партии q не менее заданного числа q₀, товар поставляется по цене c₀, где c₀<с.

Функция общих издержек С(q) задается в таком случае следующим образом:

 

Пример 3. Предположим, что интенсивность равномерного спроса составляет 1000 единиц товара в год. Организационные издержки равны 10 УЕ, издержки на хранение – 4 УЕ. Цена единицы товара равна 5 УЕ, однако, если размер партии не менее 500 единиц, цена снижается до 4 УЕ. Найти оптимальный размер партии.

Решение. Здесь

d = 1000, s = 10, h = 4, c = 5, q₀ = 500, c_o = 4.

 

Общие издержки определяются функцией С(q):

 

 

Найдем точку локального минимума. Имеем:

 

 

откуда

 

 

то

 

Поскольку

Нетрудно видеть, что функция С(q) в точке q=q₀ разрывна.

Обе функции

 

 

и

 

 

имеют минимум в точке, где

 

 

т.е. в точке

 

 

Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции С(q) в точках q и q₀, и та точка, где функция С(q) принимает меньшее значение, будет оптимальным размером партии q^* в модели поставок со скидкой (см. рис. 4, 5).

 

 

В точке q=q₀ получаем

 

 

Таким образом,

 

 

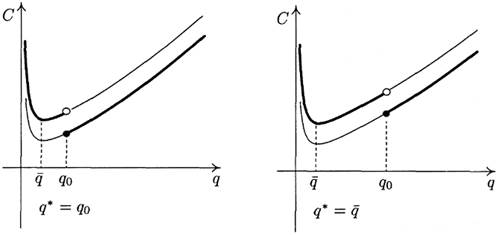
Рис. 4 Рис.5

 

Замечание. Может случиться так, что С(q) = С(q₀). Тогда в качестве q^* можно взять любое из чисел q и q₀.

 

6.5. Задания и ответы

 

1. Система управления запасами некоторого вида товара подчиняется условиям основной модели. Каждый год с постоянной интенсивностью поступает спрос на 15 тыс. единиц товара, издержки на организацию поставки составляет 10 долл. За одну партию, цена единицы товара – 3 долл., а издержки за ее хранение – 0,75 долл. в год. Найдите оптимальный размер партии.

Ответ: 632.

2. Каковы будут а) продолжительность цикла и б) число поставок за год, если стратегия управления запасами в предыдущей задаче является оптимальной?

Ответ: а) 15 дней; б) 23,7.

 

3. Система управления запасами описывается моделью производственных поставок и имеет следующие значения параметров. Спрос равен 1,5 тыс. единиц в год, цена 2 долл., издержки хранения единицы товара в течении года – 0,2 долл., организационные издержки – 10 долл. В течении года может быть произведено 4.5 тыс. единиц товара при полной загрузке производственной линии.

Нарисуйте график изменения запасов, вычислите оптимальный размер партии, продолжительность поставки, продолжительность цикла и средний уровень запасов.

Ответ: 474, 38 дней, 116 дней, 158.

4. Интенсивность спроса в модели производственных поставок составляет четверть скорости производства, которая равна 20 тыс. единиц товара в год. Организационные издержки для одной партии равны 150 долл., а издержки хранения единицы товара в течении года – 0,3 долл. Определите оптимальный размер партии.

Ответ: 2582.

5. Мебельной фирме требуется 1000 штук дверных ручек в год, расходуемых с постоянной интенсивностью. Организационные издержки составляют 30 долл. за партию, издержки на хранение одной ручки оценены в 1 долл. Цена дверной ручки составляет 2 долл., а при закупке партиями не менее 750 штук – 1,9 долл. за штуку. Найдите оптимальный размер партии поставок.

Ответ: 245.

6. Торговец имеет стабильный спрос на некоторый товар в количестве 500 единиц в год. Товар он покупает у поставщике по цене 6 долл. за штуку, причем издержки на оформление поставки и другие подготовительные операции составляет в каждом случае 10 долл. Если торговец покупает сразу партию в количестве 150 единиц товара или более,

 

цена сбавляется до 5 долл. за штуку. Каков оптимальный размер партии, если годовые затраты на хранение единицы товара равны 1 долл.?

Ответ: 150.

 

 

Глава 7

МОДЕЛЬ ЛЕОНТЬЕВА

 

В этой главе на ряде простых примеров мы покажем, как можно определить эффективность производства экономической системы по имеющейся количественной информации об объеме необходимых затрат, неизбежно сопровождающих всякое производство.

 

Продуктивные матрицы

 

Пусть имеется экономическая система, сфера производства которой состоит из n отраслей, выпускающих п видов продукта, причем каждая отрасль выпускает ровно один вид.

Предположим, что для производства fc-й отраслью единицы к-го продукта требуется а_ik ≥ 0 единиц і-го продукта, производимого і -й отраслью. Соответствующая таблица затрат выглядит так:

	1-й продукт	……	k -й продукт	……	n -й продукт
1-ая отрасль	a11	……	a1k	……	а1п
……	……	……	……	……	……
i -я отрасль	ai1	……	aik	……	ain
……	……	……	……	……	……
n -я отрасль	an1	……	ank	……	ann

 

или короче:

Полученная неотрицательная матрица А называется матрицей материальных

Пример 1. Для ответа на вопрос, является ли матрица

 

 

продуктивной, найдем ее собственные значения.

Имеем:

,

 

откуда

 

 

Корни этого уравнения легко вычисляются по формуле

 

 

и окончательно

 

λ₁ = , λ_{2 =} .

 

Тем самым,

 

λ_max = < 1.

 

Ответ: матрица А продуктивна.

затрат или технологической матрицей.

Замечание. Матрица А дает информацию о сложившейся структуре межотраслевых связей, о существующей технологии общественного производства и используется в текущем и долгосрочном планировании.

Будем считать дополнительно, что сложившаяся технология неизменна (стационарна) и что производство линейно. Последнее означает, что если для выпуска единицы /г-го продукта требуется а_ік единиц г-го продукта, то для выпуска к -го продукта необходимо а_ікх_к единиц г-го продукта.

Предположим, что за некоторый отрезок времени, фиксированный во всех дальнейших рассмотрениях (неделя, месяц, квартал или год), выпущено х₁ единиц 1-го продукта, х₂ единиц 2-го продукта, …, х_п единиц n-го продукта.

Тем самым, задан столбец

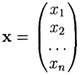
называемый столбцом выпуска или режимом работы отраслей.

При заданном столбце выпуска х совокупные затраты г-го продукта в рассматриваемой производственной сфере равны

 

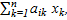i=1,…, n.

 

Из этих величин составляется столбец совокупных материальных затрат в сфере производства:

 

Из той же теоремы вытекает, что если матрица материальных затрат А продуктивна, то в любой столбец прибавочного продукта может быть произведен при соответствующем режиме работы отраслей.

Итак, пусть матрица

 

 

продуктивна

 

с =

 

- столбец конечного продукта. Покажем, как найти режим работы отраслей, обеспечивающий этот продукт.

Запишем матричное равенство

 

х – Ах = с

 

более подробно:

 

 

После перемножения:

 

 

и вычитания:

Матрица материальных затрат А ≥ 0 называется продуктивной, если найдется такой столбец выпуска х > 0, для которого выполняется неравенство

 

Ах < х.

 

Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором каждого продукта выпускается больше, чем затрачивается на его производство. Другими словами, при этом режиме сфере производства создает положительный столбец прибавочного (конечного) пункта:

 

х – Ах > 0.

 

Возникает естественный вопрос: как следует поступить, чтобы сравнительно несложным путем и как можно раньше выяснить, является ли предъявленная матрица материальных затрат исследуемой сферы производства продуктивной или, напротив, производство убыточного и совокупные материальные затраты превышают оббьем выпуска?

Справедлив следующий факт.

 

ТЕОРЕМА. Для любой неотрицательной квадратной матрицы А ≥ 0 формулируемые ниже условия равносильны.

(1) Матрица А продуктивна.

(2) Для любого столбца с > 0 существует, и притом ровно один, столбец выпуска х > 0 такой, что

 

х – Ах = с.

 

 

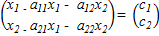
окончательно получим

 

 

Для продуктивной матрицы построенная система имеет решение при любых С₁ и С₂.

Рассмотрим конкретный пример.

Пример 2. Пусть

 

А = 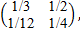с =

 

Как было установлено в примере 1, матрица А продуктивна, λ_max= < 1, и поэтому система

 

 

имеет решение (всегда совместна).

После простых преобразований получаем:

 

(3) Столбца выпуска х > 0, совокупные затраты на создание которого удовлетворяют условию

Ах ≥ х,

 

несуществует.

(4) Наибольшие собственное значение матрицы А удовлетворяет неравенству

 

λ_А = λ_max < 1.

 

Сказанное выше означает, что при выполнении хотя бы одного из этих условий выполняются и три остальных. В частности, выполнение неравенства

 

λ_А < 1.

 

позволяет утверждать, что матрица продуктивна.

В приводимых ниже примерах мы ограничимся рассмотрением случая, когда n – 2, т.е. сфера производства экономической системы состоит из двух отраслей.

 

Ограничения на ресурсы

 

Модель Леонтьева отражает те потенциальные возможности, которые заложены в технологии производственного сектора. В этой модели предполагается, что все промежуточные продукты к тому моменту, когда они оказываются необходимыми, уже произведены. Однако в реальной ситуации нужно принимать в расчет наличие таких ограничительных факторов произ-

 

и далее

 

х₁ = 12.

 

Подобным же образом, умножая первое уравнение 8 и складывая со вторым, находим значение второй неизвестной. Имеем:

 

 

Отсюда

 

х₂ = 8.

 

Таким образом, для того чтобы обеспечить прибавочный продукт

 

 

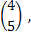
необходимо, чтобы столбец выпуска был равен

 

 

 

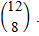
водства, как мощьность каждой отрасли (материальные ресурсы) и общее количество рабочей силы в системе (трудовые ресурсы).

Пусть L – общее число рабочих и

 

l = (l₁ l₂ ...l_n)

 

- матрица – строка затрат рабочей силы: каждый ее элемент l_k > 0 показывает количество рабочих, необходимое для производства единицы k – го продукта.

В предположении линейности производства произведении

 

 

показывает количество рабочей силы, необходимое в сфере производства при режиме работы х.

Ясно, что оно не может превосходить общего числа рабочих

 

lx ≤ L.

 

Ограничения на мощности отраслей можно описать при помощи столбца

 

 

превзойти который столбец выпуска не может,

Пример 3. Итак, даны

 

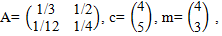
l = (4 4), L = 40.

 

Начнем с решения системы

 

х – Ах αс

 

или подробнее:

 

 

Это можно записать в равносильной форме:

 

 

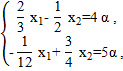
откуда

 

х ₁ = 12α, х ₂ = 8α,

 

или

х ≤ m.

 

При ограниченных ресурсах уже нельзя ставить вопрос об удовлетворении любого конечного спроса с > 0. Тем не менее продуктивная система может обеспечить любую структуру прибавочного продукта, т.е. соотношение между количеством прибавочных продуктов первой и второй отраслей.

 

ТЕОРЕМА. Пусть дана продуктивна матрица А > 0, столбцы с > 0 и m > 0, строка 1 > 0 и число L > 0. Тогда задача

имеет, и притом ровно одно, решение.

Рассмотрим на конкретном примере, как можно решить такую задачу.

 

Прибыльные матрицы

 

Предположим теперь, отрасли закупают на внутреннем рынке системы (друг у друга) продукты, которые необходимы им как средство производства.

Пусть p_i > 0 – цена единицы Г – ГО продукта. Строка

 

p = (p₁ p₂ …p_n),

каждый элемент которой является ценой единицы соответствующего

Полученный столбец должен подчиняться условиям

 

и

 

которые в данном случае принимают вид:

 

(4 4) .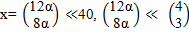

 

Отсюда имеем:

 

или

 

 

Рис.1

 

Наибольшее значение α, удовлетворяющее всем трем условиям, равно 1/3 (рис. 1).

Ответ: α_max = 1/3, столбец выпуска

 

 

конечный продукт

продукта, производимого системой, называется строкой цен на продукты или ценовой строкой.

Пусть

 

А = (а_sk)

 

- матрица материальных затрат системы. Тогда денежные издержки производства к – го продукта будут равны

 

 

Из этих величин и складывается матрица – строка рА издержек производства:

 

рА =(

 

Квадратная матрица А ≥ 0 называется прибыльной, если существует такая строка р > 0, что

 

рА < р.

 

Это означает, что существует хотя бы одна система цен р, при которой цена каждого продукта больше денежных издержек его производства и, следовательно, во всех отраслях обеспечивается положительная прибыль, выражаемая (в расчете на единицу продукции) разностью

 

р – рА.

 

Замечание 1. Соотношение между количеством первого и количеством второго прибавочного продукта 4:5 – то же, что и в случае отсутствия каких – либо ограничений на материальные и трудовые ресурсы.

Замечание 2. При n – 2 соотношения (1) принимают вид:

 

 

 

α → max

 

Решение системы уравнений можно записать так:

 

x₁ = αb₁, x₂ = αb₂,

 

где b₁ и b₂ выражаются через элементы матрицы А и столбца с.

Отсюда получаем

 

 

или, исключая α,

 

Ясно, что возможность получения прибыли неразрывно связана с возможностью получения прибавочного продукта. Более того, условия продуктивности и прибыльности матрицы (материальных затрат) равносильны и всегда справедливо соотношение

 

р (х – Ах) = (р – рА) х,

 

означающие, что прибыль есть лишь денежное выражение прибавочного продукта, а прибавочный продукт есть материальное выражение прибыли.

 

7.4. Задания и ответы

 

Сфера производства некоторой экономической системы состоит из двух отраслей. Найти оптимальный режим работы этих отраслей, обеспечивающих структуру прибавочного продукта, заданного столбцом с, при условии, что матрица материальных затрат А и строка рабочей силы 1 имеют следующий вид:

1.

и известно, что мощность первой отрасли не превосходит 24, мощность второй отрасли не превосходит 12, а общее число рабочих L равно 120;

2.

и известно, что мощность первой отрасли не превосходит 6, мощность второй отрасли не превосходит 12, а общее число рабочих L равно 90;

3.

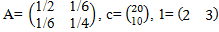
и известно, что мощность первой отрасли не превосходит 20, мощность второй отрасли не превосходит 11, а общее число рабочих L равно 72;

b₂x₁ = b₁x₂.

 

Полученное равенство на плоскости (x₁, x₂) описывает прямую, проходящую через начальную точку 0(0,0).

В свою очередь, неравенства (2) можно проиллюстрировать так, как показано на рис. 2.

Рис. 2

Рис. 3

На рис. 3 представлены все возможные случаи.

Замечание. На рис. 2 жирная точка отвечает α_max.

 

4.

и известно, что мощность первой отрасли не превосходит 12, мощность второй отрасли не превосходит 8, а общее число рабочих L равно 96;

Ответы:

1) х₁ = 14, х₂ = 12, α_max = 1/2;

2) х₁ = 8, х₂ = 8, α_max = 1/3;

3) х₁ = 20, х₂ = 10, α_max = 3/12;

4) х₁ = 12, х₂ = 8, α_max = 2/3.

 

Глава 8