Значения распределения Стьюдента

Задача № 1

 

Даны результаты измерения легирующего компонента в пробе. Найти действительное значение содержания легирующего и доверительную погрешность для Р = 0,95, при этом считать, что систематическая погрешность измерения отсутствует.

Исходные данные

Кол-во результатов	Значения переменных величин(содержание легирующего компонента в пробе xi)
	5.0
	4.5
	3.5
	4.0
	5.0
	3.5
	5.0
	4.5
	4.5
	8.0

 

Ход решения:

1)Определил среднее арифметическое измеряемой величины по формуле:

Задача № 1

 

Даны результаты измерения легирующего компонента в пробе. Найти действительное значение содержания легирующего и доверительную погрешность для Р = 0,95, при этом считать, что систематическая погрешность измерения отсутствует.

 

 

Ход решения:

1)Определил среднее арифметическое измеряемой величины по формуле:

2)Определил величину среднеквадратического отклонения:

Нашел величину и результаты занес в таблицу:

Кол-во результатов	xi	xi-X	(xi-X)2
	5.0	0.25	0.0625
	4.5	-0.25	0.0625
	3.5	-1.25	1.5625
	4.0	0.75	0.5625
	5.0	0.25	0.0625
	3.5	-1.25	1.5625
	5.0	0.25	0.0625
	4.5	-0.25	0.0625
	4.5	-0.25	0.0625
	8.0	3.25	10.563
	47.5		14.6255

 

Величина СКО равна:

3)Вычислил СКО среднего арифметического значения по формуле:

4)Для определения границ доверительного интервала, по формуле δ = ± t_p .

Необходимо найти коэффициент Стьюдента t_р для вероятности Р=0,95

Коэффициент Стьюдента равен t_р=1,96

Значения распределения Стьюдента

Доверительная вероятность Р

n 0,90 0,95 0,98 0,99 0,999

2 6,31 12,71 31,82 63,68 636,62

3 2,92 4,30 6,97 9,93 31,60

4 2,35 3,18 4,54 5,84 12,92

5 2,13 2,78 3,75 4,60 8,61

6 2,02 2,57 3,37 4,06 6,87

7 1,94 2,45 3,143,71 5,96

8 1,90 2,37 3,00 3,50 5,41

9 1,86 2,31 2,90 3,36 5,04

10 1,83 2,26 2,82 3,25 4,78

 

 

5)Конечный результат будет равен

 

Задача № 2

Определить действительное значение измеряемой величины и доверительные границы погрешности этого результата для своего варианта в предположении того, что систематические погрешности отсутствуют. Значение доверительной вероятности принять равной P = 0,95.

Исходные данные

Вариант	Ряд и кол-во измерений в ряду
	1-11; 12-14; 15-7;6-8

 

Кол-во измерений	Ряд

 

Решение:

Определил среднее арифметическое для каждого рада измерений:

Результаты вычислений внес в таблицу:

среднее арифметическое X

53,54

69,125

62,4

64,28

 

Величина (x_i-X)²

(x-X)2	6,025	50,76563	309,76	188,0816
	2,115702	66,01563	92,16	176,5102
	29,75207	37,51563	457,96	246,9388
	2,38843	523,2656	57,76	86,22449
	133,2975	141,0156	275,56	32,65306
	19,84298	62,01563	936,36	176,5102
	0,297521	102,5156	43,56	0,510204
	2,38843	123,7656	243,36
	11,93388		29,16
	0,206612		21,16
	6,479339		19,36
			0,16
			19,36
			108,16
			3893,76
Σ	214,73	1106,875	6507,6	907,4286

 

Величина СКО для каждого из рядов измерений

n-1
1/(n-1)	0.100	0,142857	0.077	0.167
σx	4,63	12,57478	42.118	18.840

 

Величина СКО среднего арифметического:

0,421261

1,571847

1,598125

1,756841

 

Вес среднего арифметического:

Коэффициент К может быть любым числом, принял К=1

Результаты вычислений в таблице:

коэффициент К
вес Р	2,373827	0,636194	0,625733	0,569203

 

Весовой коэффициент определяется по формуле:

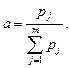
Σр	4,204958
весовой коэффициент а	0,564531	0,151296	0,148808	0,135365

 

При этом

0,564531+0,151296+0,148808+0,135365=1

Определение среднего взвешенного через веса:

 

p(i)*Xj	34,55711
X0 среднего взвешенного	58,67407

 

Дисперсиясредневзвешенного:

СКО средневзвешенного:

 

Sx-^2	0,177461	2,470703	2,554003	3,086492
1/Sx^2	5,635055	0,404743	0,391542	0,323992
Σ	6,755333
Дисперсия D(x0)	0,148031
ср.кв.откл.среднего взвешенного S	0,384748

 

Границы доверительного интервала погрешности результата (в предположении отсутствия систематической погрешности) определяются по формуле:

δ = ± , (9)

где – значение коэффициента Стьюдента, определяется по таблице (см. Приложение 2) с эффективным числом степеней свободы k_эфф равным:

k_{эфф =}

число рядов m
эффективное число степеней свободы kэфф	32,89157
коэффициент стьюдента	1,96
доверительный интервал δ	0,754107

 

Конечный результат будет равен

 

Задача № 3.1.

 

Оценить мощность измерительной цепи и погрешность этого измерения по показаниям приборов.

 

№ варианта	Амперметр, А	Вольтметр, В	Сопротивле-ниеRн, Ом
Класс точности	Диапазон измерений, А	Показание при измерении, А	Класс точности	Диапазон измерений, В	Показание при измерении, В	Номинальное значение	Погрешность D, Ом
	-	-	-	0,5	0-150			0,5

 

Решение:

По классу точности определил абсолютную погрешность амперметра и вольтметра

Вольтметр:

 

 

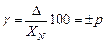Амперметр:

 

Результаты:

ΔI=δ*X/100=0,5*100/120=0,417

ΔU=X_N*γ/100=0,5*100/30=1,666667

Мощность электрической цепи вычисляется по формуле:

– среднее значение

Абсолютная погрешность косвенного измерения равна: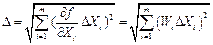

коэффициенты влияния i -го аргумента; - абсолютная погрешность измерения i -го аргумента

∂P/∂U=2*U/ 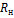=(2*120) / 30=8

∂P/∂I= (- ) = ((- )*((-1) / 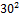) =-16

Тогда погрешность измерения равна:

Тогда конечный результат равен:

Задача № 4

Была осуществлена калибровка измерительного прибора класса точности К. Калибровка проводилась методом непосредственного сличения показаний калибруемого и образцового приборов при измерении одной и той же величины X. При этом, измеряемую величину X изменяли таким образом, чтобы указатель образцового прибора устанавливался строго на оцифрованной отметке шкалы. Результаты испытаний и характеристика калибруемого прибора приведены в таблице 11.

Рассчитайте абсолютную ∆, относительную δ и приведённую γ погрешности для каждого опыта.

Используя результаты вычислений, построить графики зависимостей ∆(х), δ(х), γ(х).

№ опыта	Показание прибора
	образцового	Калибруемого
		99,5
		300,5
		401,5
		498,5
		702,5
		801,1
		902,5

Класс точности 1

 

Абсолютная погрешность:

Δ=Х-Х_i

Относительная погрешность: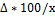

Приведенная погрешность:

X_n=10 – верхний предел измерений.

№ опыта	Показание прибора	Погрешность
	образцового	калибруемого	Δ	δ
		99,5	-0,5	-0,50251	-0,05
			-1	-0,50251	-0,1
		300,5	0,5	0,166389	0,05
		401,5	1,5	0,373599	0,15
		498,5	-1,5	-0,3009	-0,15
				0,166389	0,1
		702,5	2,5	0,355872	0,25
		801,1	1,1	0,137311	0,11
		902,5	2,5	0,277008	0,25
			-3	-0,3009	-0,3

 

№ опыта	Показание прибора	Погрешность
	образцового	калибруемого
						-1		-10
		99,5				-1	-1	-10
						-1	-2	-10
		300,5				-1	-3	-10
		401,5				-1	-4	-10
		498,5				-1	-5	-10
						-1	-6	-10
		702,5				-1	-7	-10
		801,1				-1	-8	-10
		902,5				-1	-9	-10
						-1	-10	-10

 

Графики зависимости ∆(х), δ(х), γ(х)

 

Вывод:прибор годен к работе и отклонений нет.

Задача № 5

5.1.Определить показатели унификации, если известно, что на изготовление изделий общим весом ВО, состоящего из КД деталей, из которых КУ унифицировано, общим весом ВУ, затрачено ТП чел.дней, причем трудоемкость изготовления унифицированных деталей равна СУ. Средняя стоимость нормо-часа Р рублей.

№	КД	КУ	ВО	ВУ	ТП	ТС	СД	СУ	Р
							21,4	15,3	23,5

 

Унификация – это метод стандартизации, заключающийся в рациональном сокращении количества, размеров, типов, видов, деталей, узлов и других объектов одинакового функционального назначения до количества технически и экономически целесообразного.

Уровень унификации определяется следующими показателями:

Показатель уровня унификации по количеству унифицированных деталей:

УД=(КУ/КД)×100%,

где КУ – количество унифицированных деталей; КД – общее количество деталей.

Показатель уровня унификации по весу унифицированных деталей:

УВ=(ВУ/ВО)×100%,

где ВУ – вес всех унифицированных деталей в партии; ВО – общий вес изделия.

Показатель уровня унификации по трудоемкости изготовления унифицированных деталей:

УТ=(ТС/ТП)×100%,

где ТС - суммарная трудоемкость изготовления унифицированных деталей; ТП – полная трудоемкость изготовления изделия.

НП – количество покупных деталей.

Более полную характеристику уровня унификации изделия дает комплексный показатель уровня унификации.

Этот показатель определяется как отношение части производственных затрат на изготовление унифицированных деталей к производственным затратам на изготовление всего изделия:

У=((ВУ×СУ+ТС×Р)/(ВО×СД+ТП×Р)),

где СУ - средняя стоимость единицы веса материала унифицированных деталей; СД – средняя стоимость единицы веса материала изделия в целом; Р – средняя стоимость нормо-часа.

Результаты вычислений:

УД	70,84639
УВ	69,68665
УТ	49,0566
У	0,497935

 

 

5.2.Определить ряды параметра Z,если зависимость между Z и K определяется выражениями, а также известен ряд, по которому задан параметр К.

Z=AK² / BC (1), Z = ABC/K² (2), Z = AK³ /BC (3),

Z = AВСК (4), Z = AB/CK (5), Z=AB / CK³ (6),

Исходные данные:

 

Z	K	A	B	C	ряд
	(5-10)	14,1	25,1	0,53	R40/4

 

Решение:

Нашел требуемый ряд чисел и их номера в соответствии с ГОСТ 8032 – 84

номер числа	K
	6,3

Нашел порядковые номера для чисел А,В,С

	А	В	С
номер числа			-11

 

В соответствии с формулой Z=A*B*C*K нашел порядковые номера для полученных чисел

номер числа для Z
NV1
NV2
NV3
NV4

 

Нашел числа, которые соответствуют найденным номерам и значения выражения по формуле

номер числа для Z	Значение числа	Z(4)=A*B*C*K
NV1		0,28	132,4889123
NV2		0,355	265,0276404
NV3		0,45	542,6745847
NV4		0,56	1059,911298

 

5.3Рассчитайте N значений линейного параметра в области от В₁ до В₂ по геометрической прогрессии и проведите нормализацию этого параметра. Определите ряд предпочтительных чисел, которому будут соответствовать рассчитанные значения параметра.

№	N	B1	B2
		21,2	66,8

 

Искомый ряд будет иметь следующий вид:

А; Ах; Ах²; Ах³; Ах⁴; Ах⁵; Ах⁶+ Ах⁷ + Ах⁸ + Ах⁹+ Ах¹⁰ где А=21,2; Ах¹⁰=66,8

Отсюда х = (66,8/21,2)^1/10= 1,121616– знаменатель ряда.

Вычислил значения ряда:

A	21,2
Ax^1	23,77825
Ax^2	26,67006
Ax^3	29,91356
Ax^4	33,55151
Ax^5	37,6319
Ax^6	42,20853
Ax^7	47,34175
Аx^8	53,09924
Ax^9	59,55694
Ax^10	66,8

Знаменатель полученного ряда близок к знаменателю ряда R20=1,121, а вычисленным членам ряда соответствуют следующие члены ряда R20:

20;25,28;31,5;35,5;40;45;50;56;63;71

Эти числа являются каждым восьмым членом ряда R20 в указанном диапазоне, т.е. рассчитанные нами значения линейного параметра соответствуют выборочному ряду R20/2.

 

2)Определил величину среднеквадратического отклонения:

Нашел величину и результаты занес в таблицу:

 

Значения распределения Стьюдента

Доверительная вероятность Р

n 0,90 0,95 0,98 0,99 0,999

11 6,31 12,71 31,82 63,68 636,62

12 2,92 4,30 6,97 9,93 31,60

13 2,35 3,18 4,54 5,84 12,92

14 2,13 2,78 3,75 4,60 8,61

15 2,02 2,57 3,37 4,06 6,87

16 1,94 2,45 3,143,71 5,96

17 1,90 2,37 3,00 3,50 5,41

18 1,86 2,31 2,90 3,36 5,04

19 1,83 2,26 2,82 3,25 4,78

20 1,812,23 2,76 3,174,59

21 1,80 ' 2,20 2,72 3,11 4,44

22 1,78 2,18 2,68 3,06 4,32

23 1,77 2,16 2,65 3,01 4,22

24 1,76 2,15 2,62 2,98 4,14

∞ 1,65 1,96 2,33 2,58 3,29

 

 

5)Конечный результат будет равен

 

Задача № 2

Определить действительное значение измеряемой величины и доверительные границы погрешности этого результата для своего варианта в предположении того, что систематические погрешности отсутствуют. Значение доверительной вероятности принять равной P = 0,95.

Исходные данные

Вариант	Ряд и кол-во измерений в ряду
	1-11; 12-14; 15-7;6-8

 

Кол-во измерений	Ряд

 

Решение:

Определил среднее арифметическое для каждого рада измерений:

Результаты вычислений внес в таблицу:

среднее арифметическое X

53,54

69,125

62,4

64,28

 

Величина (x_i-X)²

(x-X)2	6,025	50,76563	309,76	188,0816
	2,115702	66,01563	92,16	176,5102
	29,75207	37,51563	457,96	246,9388
	2,38843	523,2656	57,76	86,22449
	133,2975	141,0156	275,56	32,65306
	19,84298	62,01563	936,36	176,5102
	0,297521	102,5156	43,56	0,510204
	2,38843	123,7656	243,36
	11,93388		29,16
	0,206612		21,16
	6,479339		19,36
			0,16
			19,36
			108,16
			3893,76
Σ	214,73	1106,875	6507,6	907,4286

 

Величина СКО для каждого из рядов измерений

n-1
1/(n-1)	0.100	0,142857	0.077	0.167
σx	4,63	12,57478	42.118	18.840

 

Величина СКО среднего арифметического:

0,421261

1,571847

1,598125

1,756841

 

Вес среднего арифметического:

Коэффициент К может быть любым числом, принял К=1

Результаты вычислений в таблице:

коэффициент К
вес Р	2,373827	0,636194	0,625733	0,569203

 

Весовой коэффициент определяется по формуле:

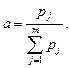
Σр	4,204958
весовой коэффициент а	0,564531	0,151296	0,148808	0,135365

 

При этом

0,564531+0,151296+0,148808+0,135365=1

Определение среднего взвешенного через веса:

 

p(i)*Xj	34,55711
X0 среднего взвешенного	58,67407

 

Дисперсиясредневзвешенного:

СКО средневзвешенного:

 

Sx-^2	0,177461	2,470703	2,554003	3,086492
1/Sx^2	5,635055	0,404743	0,391542	0,323992
Σ	6,755333
Дисперсия D(x0)	0,148031
ср.кв.откл.среднего взвешенного S	0,384748

 

Границы доверительного интервала погрешности результата (в предположении отсутствия систематической погрешности) определяются по формуле:

δ = ± , (9)

где – значение коэффициента Стьюдента, определяется по таблице (см. Приложение 2) с эффективным числом степеней свободы k_эфф равным:

k_{эфф =}

число рядов m
эффективное число степеней свободы kэфф	32,89157
коэффициент стьюдента	1,96
доверительный интервал δ	0,754107

 

Конечный результат будет равен

 

Задача № 3.1.

 

Оценить мощность измерительной цепи и погрешность этого измерения по показаниям приборов.

 

№ варианта	Амперметр, А	Вольтметр, В	Сопротивле-ниеRн, Ом
Класс точности	Диапазон измерений, А	Показание при измерении, А	Класс точности	Диапазон измерений, В	Показание при измерении, В	Номинальное значение	Погрешность D, Ом
	-	-	-	0,5	0-150			0,5

 

Решение:

По классу точности определил абсолютную погрешность амперметра и вольтметра

Вольтметр:

 

 

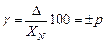Амперметр:

 

Результаты:

ΔI=δ*X/100=0,5*100/120=0,417

ΔU=X_N*γ/100=0,5*100/30=1,666667

Мощность электрической цепи вычисляется по формуле:

– среднее значение

Абсолютная погрешность косвенного измерения равна: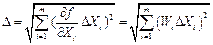

коэффициенты влияния i -го аргумента; - абсолютная погрешность измерения i -го аргумента

∂P/∂U=2*U/ 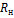=(2*120) / 30=8

∂P/∂I= (- ) = ((- )*((-1) / 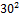) =-16

Тогда погрешность измерения равна:

Тогда конечный результат равен:

Задача № 3.2.

Расход отходящих конвертерных газов, приведенный к нормальным условиям, определяется через расход газа в рабочих условиях (Q_РУ), давление в рабочих условиях (P_РУ) и температуру в рабочих условиях (T_РУ) по формуле:

Q_НУ = (Q_РУ^. P_РУ^. T_НУ) / (T_РУ^. P_НУ) = (Q_РУ^. P_РУ^. 293) / (T_РУ^. 1013)=(0,289 ^. Q_РУ^. P_РУ) / T_РУ,

Выполнены прямые измерения в рабочих условиях расхода газа, давления, температуры и получены следующие результаты. Определить значение расхода газа Q_НУ и границы доверительного интервала при Р= 0,95

Qру, м 3/мин
Pру, гПа
Tру, К

 

Значение T_ру=2400 К необходимо проверить на грубую погрешность

Tру, К

 

Среднее значение

Значения (

(х-ср)2

 

Значение СКО:

Условие грубой погрешности:

Значение T_ру=2400 К не исключается из расчетов

Среднее значение каждого измерения

среднее	Qру, м 3/мин
	Pру, гПа	934,5
	Tру, К

 

Значение

(х-среднее)^2	Qру, м 3/мин
Pру, гПа	0,25	2,25	0,25	2,25
Tру, К

 

СКО:

скоSx	Qру, м 3/мин
	Pру, гПа	2,886751
	Tру, К

 

СКО среднего арифметического:

ско среднего	Qру, м 3/мин	17,88854
	Pру, гПа	1,443375
	Tру, К	11,180339

Q_НУ = (Q_РУ^. P_РУ^. T_НУ) / (T_РУ^. P_НУ) = (Q_РУ^. P_РУ^. 293) / (T_РУ^. 1013) =(0,289 ^. Q_РУ^.P_РУ) / T_РУ=(0,289*2197*934,5)/1610=368,54

Коэффициенты влияния:

∂Qну/∂Qру=0,286* Pру/ Tру

∂Qну/∂Рру=0,286* Q_РУ/Tру

∂Qну/∂Тру=0,286* Qру* Pру

 

∂Qну/∂Qру	0,1677456
∂Qну/∂Рру	0,394368323
∂Qну/∂Тру	-0,228905092

СКО:

Sy	3,984728239

 

Число степеней свободы:

Вместо b_i -

число степеней свободы f

7,161934009

 

Доверительный интервал: δ = ±

Коэффициент t_p=3,18 (определяется по числу степеней свободы f и вероятности Р=0,95)

доверительный интервал δ

9,762584185

 

 

Задача № 4

Была осуществлена калибровка измерительного прибора класса точности К. Калибровка проводилась методом непосредственного сличения показаний калибруемого и образцового приборов при измерении одной и той же величины X. При этом, измеряемую величину X изменяли таким образом, чтобы указатель образцового прибора устанавливался строго на оцифрованной отметке шкалы. Результаты испытаний и характеристика калибруемого прибора приведены в таблице 11.

Рассчитайте абсолютную ∆, относительную δ и приведённую γ погрешности для каждого опыта.

Используя результаты вычислений, построить графики зависимостей ∆(х), δ(х), γ(х). Для каждой зависимости строится отдельный график. На этих же графиках построить зависимости соответствующих допустимых погрешностей калибруемого прибора. Проанализировать и пояснить полученные зависимости.

Какая погрешности нормируется у данного измерительного прибора? Ответ пояснить.

№ опыта	Показание прибора
	образцового	Калибруемого
		99,5
		300,5
		401,5
		498,5
		702,5
		801,1
		902,5

Класс точности 1

 

Абсолютная погрешность:

Δ=Х-Х_i

Относительная погрешность: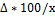

Приведенная погрешность:

X_n=10 – верхний предел измерений.

№ опыта	Показание прибора	Погрешность
	образцового	калибруемого	Δ	δ
		99,5	-0,5	-0,50251	-0,05
			-1	-0,50251	-0,1
		300,5	0,5	0,166389	0,05
		401,5	1,5	0,373599	0,15
		498,5	-1,5	-0,3009	-0,15
				0,166389	0,1
		702,5	2,5	0,355872	0,25
		801,1	1,1	0,137311	0,11
		902,5	2,5	0,277008	0,25
			-3	-0,3009	-0,3