Создать модели RLC-контура.
Перед созданием моделей задаем параметры в меню контекста L=0,01; C=0,001 и R - согласно своему варианту представленному в таблице 1.
Таблица 1
Варианты для индивидуального задания
| Вариант | ||||||||||||||
| R, Ом | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 |
Первая модель:
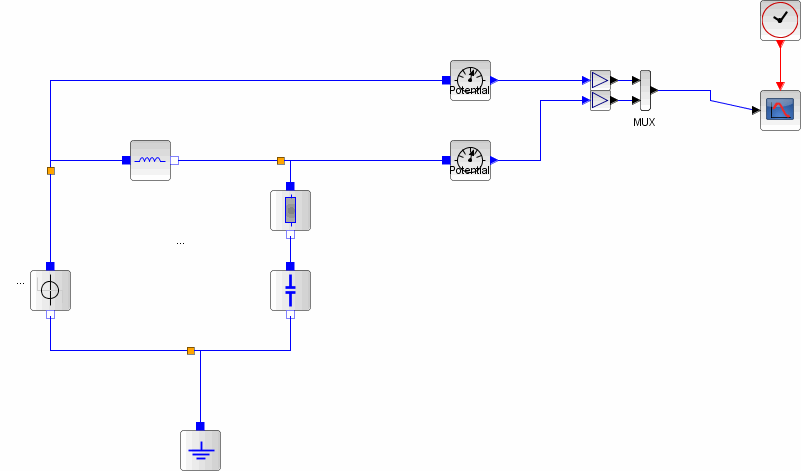
Все эти три модели объекта заданы линейным дифференциальным уравнением второго порядка, связывающим вход x (t) и выход y (t):
(*)
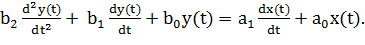Преобразуем ее в вид, соответствующей первой модели:
Uвых = UR + Uc, где: UR = iR; Uc = 1/C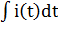 
;
Uвых = Uвх - UL, где: UL = L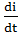 
; i = C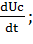 
Uвх = RC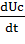 
+ Uc + LC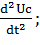 
Uвых = RC 
+ Uc;
Вторая модель.
Рассмотрим снова линейное дифференциальное уравнением второго порядка:
(*)
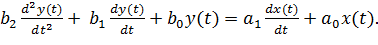Введем оператор дифференцирования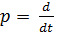 
, который действует на сигнал x (t) по правилу 
. Обратите внимание, что запись p x(t) обозначает не умножение оператора p на x(t), а действие этого оператора, то есть дифференцирование x(t).
Теперь запишем производные сигналов x (t) и y (t) по времени в операторной форме
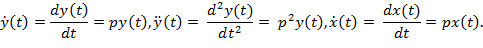
b2 p2 y(t) + b1 py(t) + b0 y (t) = a1 px (t) + a0 x (t).
Можно формально вынести за скобки y (t) в левой части равенства b x (t) в правой части:
(b2 p2 + b1 p + b0) y(t) = (a1 p + a0) x(t).
Левая часть означает, что оператор b2p2 + b1p + b0 действует на сигнал y (t), а в правой части оператор a1p + a0 действует на сигнал x (t). «Разделив» (условно, конечно) обе части на оператор b2p2 + b1p + b0, связь выхода и входа можно записать в виде
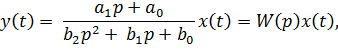
где запись W (p) x (t) означает не умножение, а действие сложного оператора
на сигнал x (t). Иначе говоря, формула y (t) = W (p) x (t) – это не что иное, как символическая запись уравнения (*), которую удобно использовать.
Функция W (p) называется передаточной функцией объекта, который описывается уравнением (*). Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
Третья модель.
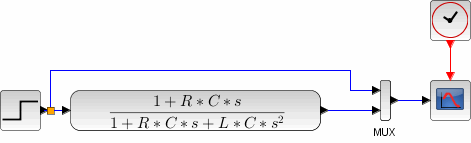
Рассмотрим снова уравнение (*):
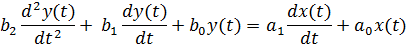
Применим к левой и правой частям преобразование Лапласа, считая, что все начальные условия нулевые. Получается уравнение в изображениях, связывающее преобразования Лапласа входа X (s) и выхода Y (s):
b2 ⋅ s2 Y(s) + b1 ⋅ sY(s) + b0 ⋅ Y(s) = a1 ⋅ sX(s) + a0 ⋅ X (s)
Можно вынести за скобки Y (s) в левой части и X (s) в правой части:
(b2s2 + b1s + b0) ⋅ Y(s) = (a1s + a0) ⋅ X(s)
Разделив обе части этого равенства на b2s2 + b1s + b0, получаем
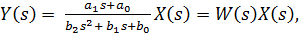где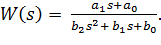 
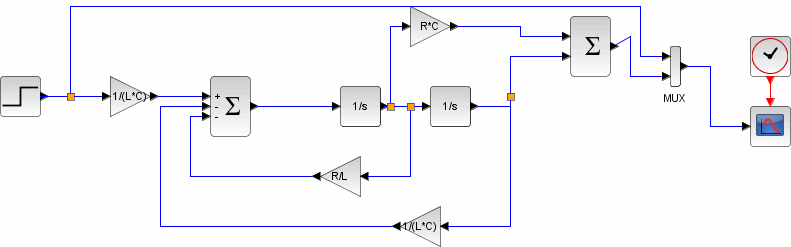
Построение диаграмм в Xcos для предыдущих 3 моделей:
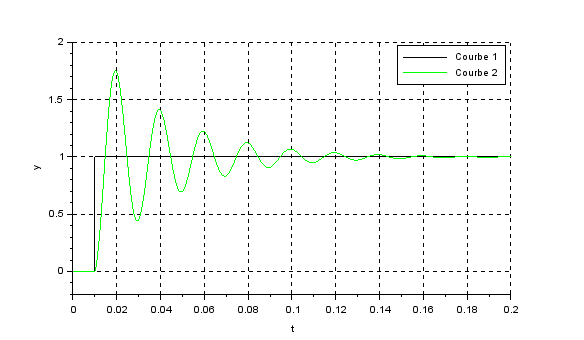
Четвертая модель.
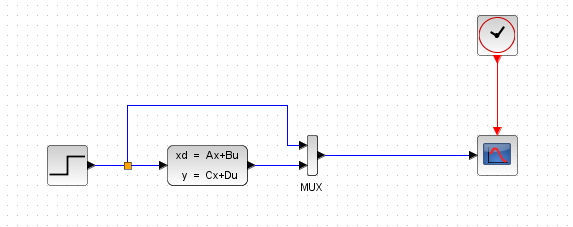
Используя преобразование Лапласа, можно построить передаточную функцию для модели объекта в пространстве состояний
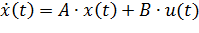
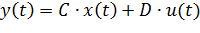
Напомним, что здесь u (t), y (t) и x (t) обозначают соответственно вход, выход и вектор состояния объекта. Преобразуя левые и правые части каждого уравнения по Лапласу (переходя к изображениям сигналов по Лапласу при нулевых начальных условиях), получаем
(**)
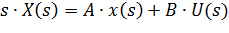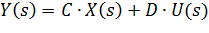
В первом уравнении перенесем все члены, зависящие от X (s), в левую часть:
(s ⋅ I − A) ⋅ X (s) = B ⋅ U (s),
где I обозначает единичную матрицу, у которой на главной диагонали стоят единицы, а все остальные элементы – нули. Умножая обе части последнего равенства на (s ⋅ I − A)−1, получим выражение для X (s):
X (s) = (s ⋅ I − A)−1 ⋅ B ⋅ U (s)
которое при подстановке во второе уравнение в (**) дает
Y (s) = C ⋅ (s ⋅ I − A)−1 ⋅ B ⋅ U (s) + D ⋅ U (s) = [ C ⋅ (s ⋅ I − A)−1 ⋅ B + D ]⋅ U (s).
Чтобы определить передаточную функцию, найдем отношение изображений выхода и входа:
Обратный переход, от передаточной функции к модели в пространстве состояний, более сложен и неоднозначен. Дело в том, что каждой передаточной функции соответствует бесчисленное множество моделей в пространстве состояний. Одну из них можно найти следующим образом. Для передаточной функции
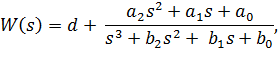
где d, ai (i = 0,1,2) i и b (i = 0,1,2) – постоянные коэффициенты, модель в пространстве состояний задается матрицами
Так как b0 =-1, b1=R/C, b2=L/C, a0=1, a1=R/C, a2=0, d=0, матрицы будут иметь вид:
Построение диаграммы:
Пятая модель.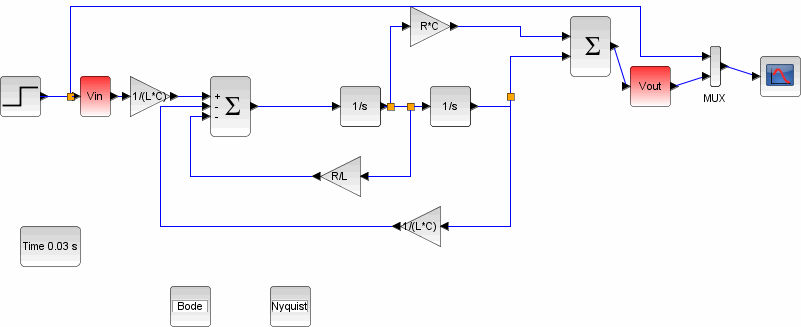 
В блоке GRANDEUR_PHYSIQUE меняем значения с «Nom» на «Vin» и «Vout». А в блоках REP_TEMP и REP_FREQ вставляем значения как показана на рисунках ниже:
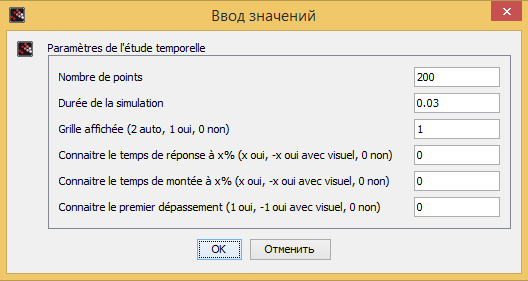
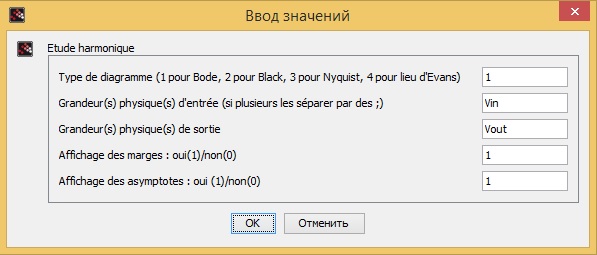
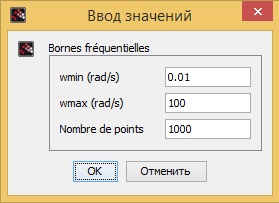
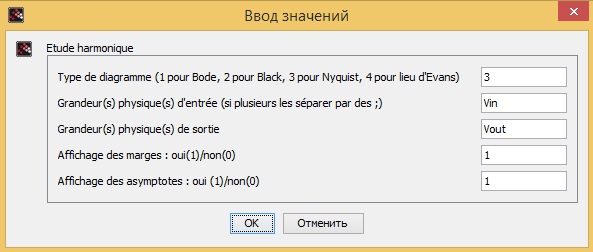
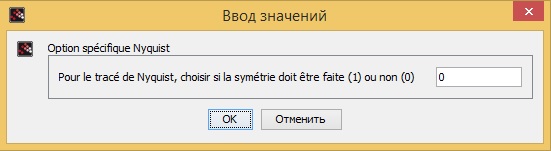
Построение диаграмм в Xcos.
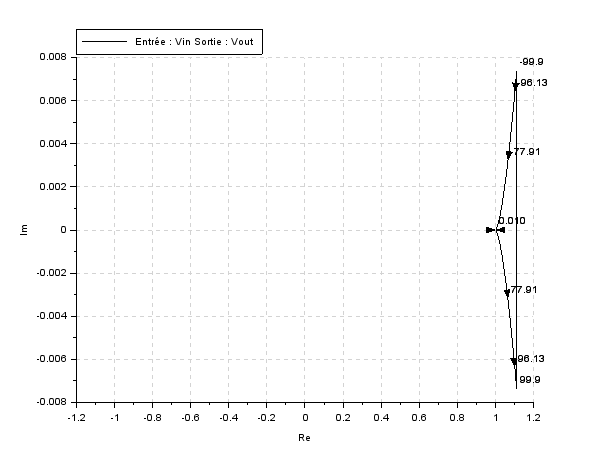
Кривая Найквиста
Частотная придаточная функция разомкнутой системы представляет собой комплексное число.
Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с придаточной функцией W(p). Если изменять частоту входного воздействия от –∞ до +∞ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудную – фазовую характеристику разомкнутой системы. Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси
