Прибор состоит из широкой пробирки с отводом. Через тройник-отводник пробирки соединяются с одной стороны с манометром, а с другой - через двугорлую склянку с насосом. Пробирка плотно закрывается пробкой, в которую вставлен термометр. Пробирка опускается в водяную баню, которая медленно нагревается.
В пробирку наливают 5-10мл испытуемой жидкости (изопропиловый спирт), пробирка плотно закрывается пробкой с термометром. Шарик термометра должен находиться примерно на 1 см выше уровня жидкости. После этого пробирку соединяют с насосом и манометром.
Перед началом работы необходимо проверить прибор на герметичность. Для этого с помощью насоса создают в приборе произвольное разряжение, не доводя жидкость до кипения, и наблюдают за уровнем ртути в манометре. Если в течение нескольких минут положение ртути не изменится, то систему можно считать герметичной. В противном случае необходимо проверить все соединения в приборе и добиться полной его герметичности. Только после этого можно начинать опыт.
Выдержав жидкость несколько минут при данной температуре насосом создают такое разряжение, что жидкость в приборе закипает. В этот момент делают отсчеты температуры и снимают показания манометра. Если испытуемая жидкость-эфир, то отсчет производят при комнатной температуре, этиловый спирт - при 700 С. После отсчета осторожно выпускают воздух через кран, снижают разряжение примерно на 100 мл и медленно нагревают воду, пока жидкость снова не закипит. Сделав отсчеты как в первом случае, снова снижают разряжение и повторяют измерения. Так поступают несколько раз. Последнее измерение проводится при атмосферном давлении, на этом опыт заканчивается.
Полученные данные сводятся в таблицу 2.
Таблица 2
| Показания манометра | Температура кипения жидкости |
По данным столбцов строится график зависимости  от
от 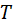 . Рассчитывается молекулярная теплота испарения по уравнению Клаузиуса - Клапейрона в интеграле двух температур. Температура выбирается так, чтобы разница между ними была не менее 8-120С.
. Рассчитывается молекулярная теплота испарения по уравнению Клаузиуса - Клапейрона в интеграле двух температур. Температура выбирается так, чтобы разница между ними была не менее 8-120С.
Для построения графика 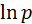 от
от  и расчета из него молярной теплоты испарения необходимо составить таблицу 3.
и расчета из него молярной теплоты испарения необходимо составить таблицу 3.
Таблица 3
| tкип (С0) | Ткип (К) | 1/T | Рмм.рт.ст. | lnP |
Данные строк наносятся на миллиметровую бумагу в строго выбранном масштабе. Через полученные точки проводится усредненная прямая и рассчитывается тангенс угла наклона ее по любым двум произвольно взятым точкам на этой прямой.
В этом случае
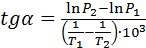 (17)
(17)
 и
и 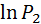 и соответствующие им значения
и соответствующие им значения  и
и  берутся из графика по масштабу.
берутся из графика по масштабу.
Уравнение Клаузиуса – Клапейрона
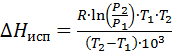 (18)
(18)
R=1,988 кал/моль.град = 8,314Дж/мольК
Теплота испарения может быть найдена, кроме того, по графику
 (19)
(19)
При построении строго соблюдать масштаб - единичный отрезок по горизонтальной и вертикальной оси должен быть одинаковый.
Рис. 3.
Контрольные вопросы
1. Используя измеренную зависимость давления насыщенного пара от температуры, рассчитайте температуру кипения исследуемой жидкости и сравните с табличным значением.
2. При заданной преподавателем температуре рассчитайте изменение внутренней энергии ∆U, энтропии ∆S, термодинамического потенциала ∆G, свободной энергии ∆F при испарении 1 моля исследуемой жидкости.
3. Используя табличные данные, рассчитайте стандартную энтропию 1 моля исследуемого вещества в жидком и газообразном состоянии при заданной преподавателем температуре.
4. Используя данные Приложения, рассчитайте давление насыщенного пара над льдом при температуре – 10°С или другой заданной температуре.
Лабораторная работа №6
Термический анализ
Цель работы:
1. Изучить основные положения гетерогенного равновесия;
2. Освоить простейшую методику термодинамического анализа двухкомпонентных систем;
3. Научится строить диаграммы состояния бинарных систем по кривым охлаждения и анализировать их с помощью правила фаз Гиббса.
Теоретическая часть
Системы, в которых отсутствуют вещества в газообразном состоянии, называются конденсированными. В таких системах возможны как химические, так и фазовые превращения, заканчивающиеся достижением состояния фазового равновесия.
Для фазового равновесия гетерогенных систем, состоящих из любого числа фаз и любого числа компонентов, Гиббсом в 1876 году выведен закон равновесия фаз (правило фаз Гиббса), основными понятиями которого являются термодинамическая степень свободы и число независимых компонентов.
Под термодинамической степенью свободы понимается параметр, произвольное изменение которого не изменяет ни числа, ни вида фаз системы, т.е. не нарушает фазового равновесия. Число параметров состояния, которые можно произвольно изменять, не нарушая фазового равновесия, называется числом степеней свободы системы или ее вариантностью.
Правило фаз Гиббса (закон равновесия фаз) имеет следующее математическое выражение:
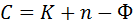 (36),
(36),
где 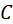 – число степеней свободы;
– число степеней свободы;
 – число независимых компонентов;
– число независимых компонентов;
 – число параметров, общих для всех фаз системы (чаще всего это P и T, одинаковые для всех фаз системы, находящейся в состоянии равновесия);
– число параметров, общих для всех фаз системы (чаще всего это P и T, одинаковые для всех фаз системы, находящейся в состоянии равновесия);
 – число фаз системы.
– число фаз системы.
Закон равновесия фаз формулируется так: число степеней свободы равновесной термодинамической системы равно числу независимых компонентов плюс число параметров, общих для всех фаз системы, минус число фаз.
В конденсированных системах изменяющимся параметром, общим для всех фаз, является температура (давление на жидкие и твердые вещества практически не влияет), поэтому правило фаз приобретает вид:
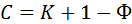 (37).
(37).
Графическое изображение состояния системы при различных параметрах называется диаграммой состояния. С помощью такой диаграммы в виде геометрических образов наглядно изображается характер взаимодействия компонентов в жидком и твердом состояниях, границы существования фаз, их состав и др.
Диаграммы состояния строятся в координатах состав – свойство. Для двухкомпонентных систем на оси абсцисс откладывается состав, а на оси ординат – свойство. При изучении кристаллизации из растворов обнаружено, что температуры начала и окончания кристаллизации зависят от состава раствора. Диаграммы, выражающие зависимость температур начала и конца кристаллизации от состава называются также фазовыми диаграммами или диаграммами плавкости. На таких диаграммах состав на оси абсцисс выражается в массовых, мольных или атомных процентах, а температура на оси ординат – в градусах Цельсия (t °C), но возможно применение и любой другой температурной шкалы.
Точка, указывающая на фазовой диаграмме состояние системы при заданных параметрах, называется фигуративной.
Следует иметь в виду, что на диаграмму состояния наносятся не любые
точки, а лишь те, которые соответствуют фазовым превращениям, таким как
кристаллизация, перекристаллизация, расслаивание жидкости и др.
Совокупности таких точек образуют определенные линии, имеющие
собственные названия. Так, линия, являющаяся совокупностью точек начала
кристаллизации, носит название линии ликвидуса (т.е. жидкости) или просто
ликвидус. Линия, отвечающая температурам конца кристаллизации (полного
затвердевания), называется линией солидуса (т.е. твердого тела) или просто
солидусом. Выше ликвидуса в системе нет кристаллов, ниже солидуса нет жидкости.
Многокомпонентные системы, образующие несколько фаз, изучаются
методами физико-химического анализа.
Одним из наиболее распространенных его видов является термический
анализ, сущность которого состоит в определении температур фазовых
превращений путем анализа так называемых кривых охлаждения. Кривыми
охлаждения называются кривые, изображающие зависимость температуры
системы от времени охлаждения. Получаются они опытным путем. Для этого
чистое вещество или смесь веществ определенного состава нагревают до
жидкого состояния, а затем непрерывно и равномерно охлаждают, фиксируя
температуру системы через равные промежутки времени. Полученные
данные изображаются в виде кривой, построенной в координатах
«температура (T) – время (t)».
Метод термического анализа основан на изучении изменении температуры системы в зависимости от времени охлаждения. В результате получаются кривые охлаждения. Вид их зависит от состава и типа смеси.
Экспериментальная часть
Для построения диаграммы плавкости и определения эвтектической точки двухкомпонентной системы «бензойная кислота – стеариновая кислота»в шесть пробирок помещают исследуемые смеси этих веществ. Состав смесей соответствует табл. 1.
Таблица 1
Процентное соотношение бензойной и стеариновой кислот
| Пробирки | ||||||
| бензойная кислота | ||||||
| стеариновая кислота |
Общий вес смеси в пробирке составляет 5 г. Пробирки по очереди помещают в воздушную баню (рис. 1). После того, как содержимое пробирки расплавится и несколько перегреется (см. табл. 2), ее переносят в коническую колбу, играющую роль воздушной рубашки, помещенную в водяную баню, температуру которой поддерживают 15 – 170С. Затем ведут наблюдение за смесью с помощью КСМ, который автоматически пишет диаграмму (кривые охлаждения) «температура-время». Таким образом, на 6 смесей получаем 6 кривых охлаждения. На их основании строим диаграмму двухкомпонентной системы и затем диаграмму плавкости двухкомпонентной системы бензойной и стеариновой кислот.
Таблица 2
Температура нагрева – охлаждения смеси в пробирках, 0С
| № пробирки | ||||||
| нагрев | ||||||
| охлаждение | 30 – 40 | 30 – 40 | 30 – 40 | 30 – 40 |

Рис. 1. Схема установки
Задание
1. На листе миллиметровой бумаги построить по кривым охлаждения диаграмму состояния в координатах температура-состав.
2. Дать название полученной диаграмме.
3. Охарактеризовать её.
4. Рассчитать криоскопическую константу обоих веществ по формуле:
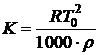 ,
,
где Т0 – температура кристаллизации чистого вещества;
r - удельная теплота плавления 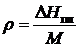 ;
;
М – молярная масса (г/моль).
5. С помощью уравнения Шредера рассчитать теплоты плавления обоих веществ:
 (1).
(1).
Если известны температуры кристаллизации двух растворов разного состава, то с помощью уравнения (1) можно рассчитать теплоту плавления кристаллизующегося вещества.
Обычно в качестве одной жидкости берут чистое вещество, а в качестве другого – раствор, содержащий небольшое количество другого вещества. Тогда из уравнения (1):

где DН пл – теплота плавления кристаллизующегося вещества;
Т0 – температура плавления чистого вещества А;
Т – температура плавления раствора, содержащего кроме А небольшое количество другого вещества;
ХА – мольная доля вещества А в растворе.
Вопросы:
1. Правило фаз Гиббса.
2. Диаграммы состояния однокомпонентных систем.
3. Неизоморфные системы:
а) Диаграмма состояния неизоморфной системы с простой эвтектикой. Правило рычага, треугольник Таммана;
б) Диаграммы состояния неизоморфных систем с образованием устойчивых химических соединений;
в) Диаграмма состояния неизоморфных систем с образованием неустойчивых химических соединений;
4. Изоморфные системы. Диаграммы состояния.
2.5. Правила работы с термометром Бекмана
 Термометр Бекмана (рис.5) отличается от обычного, во-первых, точной шкалой, позволяющей наблюдать изменения температуры до 0,002 0С, а во-вторых, вторым запасным ртутным резервуаром 1, при помощи которого можно менять количество ртути в основном, нижнем резервуаре 2 и тем самым значительно расширять диапазон измеряемых температур. Шкала такого термометра, имеющего длину 25 - 30 см, поделена всего на 5 0С с отметками между ними десятых и сотых долей.
Термометр Бекмана (рис.5) отличается от обычного, во-первых, точной шкалой, позволяющей наблюдать изменения температуры до 0,002 0С, а во-вторых, вторым запасным ртутным резервуаром 1, при помощи которого можно менять количество ртути в основном, нижнем резервуаре 2 и тем самым значительно расширять диапазон измеряемых температур. Шкала такого термометра, имеющего длину 25 - 30 см, поделена всего на 5 0С с отметками между ними десятых и сотых долей.
Переводя некоторое количество ртути из нижнего резервуара в верхний, или наоборот, всегда можно настроить термометр так, чтобы температура раствора попадала бы на ту часть этой условной шкалы, на которой нам удобно работать.
Чтобы настроить термометр Бекмана, вначале необходимо опустить его в исследуемый раствор и посмотреть, где установится ртуть.
Если столбик ртути опустится ниже шкалы, то необходимо привести в соприкосновение ртуть обоих резервуаров.
·  Подогревая рукой (а если этого недостаточно, то опуская термометр в теплую воду), вызывают расширение ртути в нижнем резервуаре с тем, чтобы заполнить ею весь капилляр доверху.
Подогревая рукой (а если этого недостаточно, то опуская термометр в теплую воду), вызывают расширение ртути в нижнем резервуаре с тем, чтобы заполнить ею весь капилляр доверху.
· Быстро перевернув термометр головкой вниз и, слегка постучав по ней рукой, добиваются того, чтобы ртуть в запасном резервуаре подошла вплотную к верхушке капилляра, наполненного ртутью из нижнего резервуара, и слилась с ней.
· Термометр осторожно (чтобы не разорвать ртуть) возвращают в прежнее вертикальное положение.
·
|
· Затем быстро вынимают термометр из охлаждающей смеси и, слегка ударив его об указательный палец свободной руки, вызывают разрыв между ртутью в верхнем резервуаре и ртутью, находящейся в капилляре.
· Чуть-чуть подогрев рукой нижний резервуар, вызывают расширение ртути, что замечают по небольшой капельке ртути, которая появляется у конца капилляра в верхнем резервуаре. Легким ударом эту капельку стряхивают в верхний резервуар. Термометр вновь помещают в стакан с исследуемым раствором.
Если температура на шкале термометра окажется в удобных пределах, то термометр считается настроенным. Если показания термометра выше, то стряхивание ртути повторяют. Если ниже, то настройку термометра начинают сначала /9-12/.
2.6. Вычисление Dt
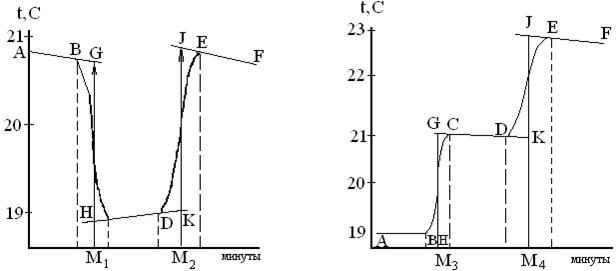
а б
Рис. 6. Изменение температуры для: а – эндотермических процессов,
б – экзотермических процессов
Каждый калориметрический опыт начинают с определения температурного хода калориметрической системы. Для этого в течение нескольких минут измеряют температуру установки (участок АВ на рис. 6).
Участок ВСна графиках соответствует собственно реакции: эндотермической (на рис. 6, а) и экзотермической (на рис.6,б). В результате реакции наблюдается значительное изменение температуры калориметра (DT1). Окончание реакции регистрируется после того, как изменение температуры в калориметре прекратится или станет медленным и равномерным (участок CD).
Наличие небольшого наклона на графике температурной зависимости в начальном (АВ) и конечном (CD) периодах свидетельствует о том, что во время опыта имеет место некоторый теплообмен калориметра с окружающей средой. В расчетах теплообмен учитывается следующим образом. Прямая АВ экстраполируется вправо, а прямая СВ влево. Интервал времени от В до С делится пополам и через эту точку проводится перпендикуляр к оси абсцисс до пересечения его с экстраполированными участками прямых АВ и СD (точки H, G). Величина отрезка HG соответствует изменению температуры калориметрической системы DT1, связанному непосредственно с реакцией.
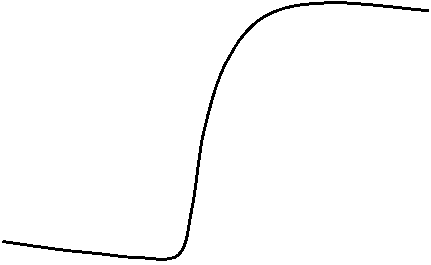
Порядок определения ∆t.
 t,0С
t,0С
t2
     C / C /
| E | С | D | ||||||||||
 K K
| 1 | P | |||||||||||
  B / B /
| А | B | |||||||||||
 t1 t1
| F | ||||||||||||

|
0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 5,5 6 Т,мин
Рис. 7. Построение графика зависимости температуры от времени
Типичный вид температурной кривой правильно поставленного калориметрического опыта при измерении экзотермического эффекта показан на рис.5.
Расчет величины с учетом теплообмена может быть произведен или аналитическим, или графическим способом.
При графическом определении Dt на миллиметровой бумаге на оси абсцисс откладывают время в масштабе 0,5 мин =1см, на оси ординат - температуру, выбор масштаба которой зависит от величины Dt: если Dt< 1, то 1°=10см; при Dt>1 принимают1°=5 см.
После того, как на график нанесены все экспериментальные точки, получается кривая ABCD.
Участок АВ называется начальным периодом, ВС - главным, CD – конечным.
Чтобы определить изменение температуры Dt, не искаженное тепловым обменом, происходящим в течение главного периода, проводят касательные к линиям АВ и CD. Точки В и С, соответствующие начальной и конечной температурам главного периода, наносят на ось ординат (точки В/ и С/). Через середину отрезка В/С/ проводят линию КР, параллельную оси времени. Пересечение этой линии с кривой ВС дает точку 1, из которой восстанавливают перпендикуляр к оси абсцисс. Отрезок перпендикуляра EF, отсекаемый касательными, и будет равен Dt.
Характер линии ВС зависит от условий протекания теплового процесса, например от размешивания. Наклон линий АВ и CD зависит от характера теплообмена с окружающей средой. Таким образом, по виду кривой ABCD можно судить о качестве проведенного опыт.